
Конспек лекцій ВНС
.pdfконкретну систему окремих аркушів розграфлених і кодованих відповідно до національних вимог. Всі аркуші зазвичай створені в єдиній картографічній проекції, мають уніфікований зміст і картографічний дизайн. Наприклад, в радянський період серії аркушів топографічних карт / планів створювалися в масштабах 1: 500, 1: 1000, 1: 2000, 1: 5000,1: 25000, 1: 50000, 1: 100000, 1: 200000, 1: 500000 і 1: 1000000. Цей масштабний ряд серії топографічних карт зі стандартними розграфленням та номенклатурою досі використовується в деяких колишніх радянських республіках, включаючи Україну.
Міжнародна UTM система прийнята в багатьох країнах при виробництві національних топографічних карт.
МАТЕМАТИЧНА КАРТОГРАФІЯ
1. Предмет і задачі математичної картографії.
Математична картографія вивчає питання зображення математичної поверхні Землі, Місяця, планет і зоряного неба на площині з метою створення різноманітних карт та розв’язання по ним теоретичних і практичних задач картографії, геодезії, астрономії, навігації та інших галузей науки та виробництва, а також для цілей оборони країни.
Поверхня картографування Землі і планет має складну конфігурацію і неправильну геометричну форму. Тому, щоб відобразити її на площині, необхідно від фізичної поверхні перейти до математичної, яка була б близькою до фізичної і виразити її формулами, тобто побудувати в тій чи іншій картографічній проекції. Для того, щоб проводити виміри по карті необхідно знати картографічну проекцію, в якій вона складена та закони розподілу спотворень (масштабів, довжин, площ, кутів).
Предметом математичної картографії є математична основа карти, проектування якої – перший етап в процесі створення карт. Для вирішення цієї задачі використовуються певні математичні закони, які встановлюють зв’язок координат точок на поверхні Землі і на площині, тобто вибирають ту чи іншу картографічну проекцію і будують відповідну картографічну сітку (частіше всього меридіанів і паралелей), розглядають питання масштабу, їх вимірювань, розграфки і номенклатури
Основними задачами математичної картографії є:
а) розвиток теорії математичної картографії, перш за все це отримання найкращих картографічних проекцій;
б) дослідження картографічних проекцій, їх властивостей і доцільності їх використання на практиці;
в) вдосконалення існуючих картографічних проекцій;
г) розробка математичних елементів карт (компонування, рамок і номенклатури для багатоаркушевих карт);
ґ) вивчення способів та засобів вимірювань на карті;
д) вивчення та розв’язання задач математичного характеру, що виникають при укладанні карт.
2. Зображення поверхні еліпсоїда обертання і кулі на площині.
В математичній картографії поверхні картографування (Земля, Місяць, планети) приймають за кулю, або за еліпсоїд обертання (для Землі), мала вісь якого співпадає з віссю обертання Землі.
При укладанні карт еліпсоїд обертання або куля повинна бути відображена на площині. Жодна з цих поверхонь не може бути розгорнута без складок або розривів. Тому при укладанні карт використовуються картографічні проекції, в яких зображення поверхні на площину виконується за певними математичними законами. Ці закони виражають функціональний зв’язок між координатами

точок поверхні і площини. В основі такого відображення поверхні, яку картографують, лежить система географічних або геодезичних координат, координатними лініями яких є меридіани і паралелі.
Лінії меридіанів одержують шляхом січення поверхні еліпсоїда (кулі) площинами, які проходять через вісь обертання (для еліпсоїда обертання меридіанами будуть еліпси, а для кулі – кола), а лінії паралелей – шляхом січення поверхні, яку картографують, площинами перпендикулярними до осі обертання (мають вигляд кола).
Положення меридіанів і паралелей на поверхні визначається криволінійними географічними або геодезичними координатами: широтою φ і довготою λ (або B і L).
На кулі і еліпсоїді лінії постійних широт та довгот утворюють сітку меридіанів і паралелей, яку називають географічною, і яка є ортогональною (меридіани і паралелі перетинаються під прямим кутом).
Еліпсоїд обертання характеризується великою піввіссю а (екваторіальною) і малою віссю b (полярною), а також стиснення α і ексцентриситетами е (першим) та е' (другим). При цьому: α = (а- b)/а, е2= (а2-b2)/а2, е'2= (а2-b2)/b2.
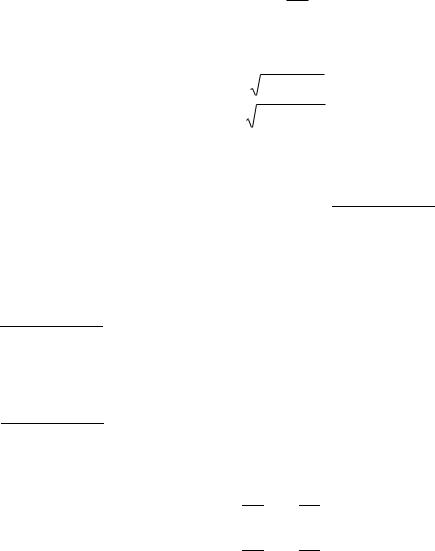
Кривизна поверхні еліпсоїда обертання характеризується радіусом кривизни, два з яких прийняті за головні – радіус кривизни меридіана М, що знаходиться в площині обертання Землі, та радіус кривизни першого вертикала N, який знаходиться в площині екватора. Вони визначаються за формулами :
|
a(1 e |
2 |
) |
|
|
|
|
a |
|
|
||
M |
|
|
; |
N |
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 e |
2 |
sin B) |
3 |
|
(1 e |
2 |
sin |
2 |
B) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2
середній радіус кривизни R, та радіус паралелі r визначаються за формулами :
R |
MN |
r N cos B |
Рівняння меридіанів λ=const |
|
Рівняння паралелей φ=const |
|
Враховуючи викладене вище |
|
Загальні рівняння картографічних проекцій мають вигляд: |
|
х = f1(φ,λ) |
(1) |
|
|
у = f2(φ,λ) |
|
Де φ і λ – криволінійні географічні координати деякої точки на поверхні картографування; х і у – прямокутні координати зображення цієї точки на площині в проекції, яка визначається функціями f1 і f2 за умови, що ці функції однозначні і неперервні(разом зі своїми частковими похідними).
Властивості проекції будуть залежати від властивостей і характеру функцій f1 і f2. Оскільки цих функцій буде безліч, то і проекції можуть бути різноманітними.
Кожній проекції відповідає певна картографічна сітка меридіанів і паралелей, яка складає математичну основу карти.
Положення меридіанів та паралелей на поверхні картографування визначається криволінійними географічними координатами: широтою φ, та довготою λ.
Якщо виключити з рівнянь (1) широту φ отримаємо рівняння меридіанів на площині (в проекції):
F1 (x, у, λ) = 0, |
(2) |
а виключивши довготу λ – рівняння паралелей:
F1 (x, у, φ) = 0. |
(3) |
Якщо допустити, що φ=φ0=const, то з рівняння (1) одержимо рівняння паралелей в параметричній формі
х = f1(φ0,λ) |
у = f2(φ0,λ) (4) |
Якщо допустити, що λ=λ0=const, то з рівняння (1) одержимо рівняння меридіанів в параметричній формі
х = f1(φ,λ0) |
у = f2(φ,λ0) (5) |
Зображення ліній меридіанів та паралелей в проекції називають картографічною сіткою.
Якщо х = f1(φ), у = f2(λ) (6), то паралелі і меридіани прямі, взаємно перпендикулярні лінії. Картографічна сітка буде мати найбільш простий вигляд.
Якщо х = f1(φ), у = f2(φ,λ) (7), то паралелі зображені прямими лініями по осі у (паралельні осі у), а меридіани – кривими.
Якщо х = f1(φ,λ), у = f2(λ) (8), то меридіани зображені прямими лініями по осі х (паралельні осі х), а паралелі – кривими.
І, нарешті, якщо х = f1(φ,λ), у = f2(φ,λ), то можна отримати проекції з різноманітними криволінійними картографічними сітками вид яких залежатиме від f1 та f2.
Зображенням поверхні землі на площині в будь-якій проекції притаманні спотворення (довжин, площ, кутів). При чому ці спотворення залежать від властивостей зображення. В одних проекціях можна позбутися спотворення площ, в інших кутів, але довжини ліній будуть спотворені у всіх проекціях (спотворення довжин відсутні тільки в окремих точках або на деяких лініях карти).
Кожна карта має головний масштаб μ0, який показує загальне зменшення всієї поверхні картографування (або її частини) при зображенні на площині. Він підписується на карті, проте зберігається лише в окремих її точках або на деяких лініях.
При дослідженнях картографічних проекцій головний масштаб μ0 як правило приймається за одиницю, так як він не впливає на властивості картографічної проекції.
Оскільки масштаб на карті є величиною змінною, тому введене поняття часткових масштабів, довжин і площ в даній точці і в заданому напрямку.

Частковим масштабом довжин називають співвідношенням довжин безмежно малого відрізка на карті (в проекції) dS’ до довжини відповідного безмежно малого відрізка на поверхні, яку картографують (еліпсоїда чи кулі) dS:
|
dS |
(9) |
|
dS |
|||
|
|
Частковий масштаб довжин є функцією географічних координат φ та λ, які визначають положення
точки на |
поверхні картографування та азимуту (α) напряму, по якому визначається частковий |
|
масштаб: |
μ = F1 (α,φ,λ) |
(10) |
Надалі часткові масштаби будемо називати масштабами за напрямками. Наприклад для меридіану: α=0° або α=180° μ=m – масштаб вздовж меридіану; для паралелі: α=90° або α=270° μ=n – масштаб вздовж паралелі.
Спотворенням довжин (Vμ) називається різниця між частковим масштабом довжин та одиницею, яка виражається в відсотках, наприклад коли:
-масштаб довжин вздовж меридіанів m = 1.22, тоді Vm = (m – 1)·100% = +22%,
-масштаб довжин вздовж паралелей n = 0.75, тоді Vn = (n – 1)·100% = -25%.
Частковим масштабом площ називається відношення безмежно малої площі (елементарної ділянки) на карті (в проекції) dF′до відповідної безмежно малої площі на поверхні, яку картографують (еліпсоїда чи кулі) dF:
p |
dF |
(11) |
|
dF |
|||
|
|
Як правило dF' ≠ dF, проте можуть існувати такі проекції, в кожній точці яких dF' = dF (рівновеликих еквівалентних за характером спотворень).
Частковий масштаб площ залежить від географічного положення елемента площ
р = F2 (φ,λ) (12)
Спотворення площ (Vр) називається різницею між масштабами площ і одиницею, яка виражається у відсотках р = 1.43, тоді Vр = (р – 1)·100% = +43%
Спотворення кутів (ΔU) характеризується різницею між величиною кута в проекції (U') і відповідним кутом на поверхні картографування (U). Як правило U' не дорівнює U, але можуть існувати такі проекції, в кожній точці яких U' = U (рівнокутні (конформні) проекції).
Спотворення U=U′-U (13) є функцією географічних координат і азимутів напрямків.
ΔU=F3(φ,λ,α).
В якості міри кутових спотворень використовують найбільше спотворення кутів:
ΔUmax = ω=2(α-β)
де β – зображення азимута α в проекції і у вказаному напрямку.
Величини спотворень є одними з основних критеріїв оцінки властивостей картографічних проекцій.
3. Частковий масштаб довжин. Масштаб вздовж меридіанів та паралелей.
Масштаб довжин за формулою 9 рівний:
dS dS
,
Їз елементарного сфероїдичного трикутника (рис. 1,2)
dS |
dx |
2 |
dy |
||
|
|
|
|
||
dS |
dS |
2 |
dS |
||
m |
|||||
|
|
|
|||
2
2 n
(14)
dS |
m |
|
В цьому трикутнику нескінченно мала дуга меридіану рівна :
|
a(1 e |
2 |
) |
|
||||
Md (15), де М – радіус кривизни меридіану M |
|
|
||||||
(1 e |
2 |
sin |
2 |
) |
3 / 2 |
|||
|
||||||||
|
|
|
|
|||||
Нескінченно мала дуга паралелі визначається за формулою:
(по теоремі Меньє);
dS |
n |
rd |
|
|
|
|
|
( N |
e |
||
|
|
(1 |
|
(16), де r – радіус кривизни паралелі (r = Ncosφ), а N – радіус кривизни першого вертикалу
|
a |
|
|
|
). |
|
2 |
sin |
2 |
) |
1/ 2 |
||
|
||||||
|
|
|
|
Згідно з вище викладеними виразами запишемо :
|
|
|
dx |
2 |
dy |
2 |
|
|
||||
|
2 |
|
|
|
|
|
(17), де згідно з (1) (зазальні рівняння картографічних проекцій) повні |
|||||
|
|
|
|
|
|
|
|
|
||||
|
2 |
d |
2 |
r |
2 |
d |
2 |
|||||
|
|
M |
|
|||||||||
|
|
|
|
|
|
|
|
|||||
диференціали для dx та dy будуть мати вигляд:
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
dx |
|
d |
dx |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(18) |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
d |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
звідси: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(dS ) |
2 |
|
2 |
|
2 |
|
|
x |
|
|
|
|
x |
|
|
2 |
|
|
y |
|
y |
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
dx |
|
dy |
|
|
|
|
|
|
d |
|
|
|
d |
|
|
d |
|
|
d |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
2 |
|
2 |
|
|
x x |
|
|
|
|
x |
2 |
|
2 |
|
|
|
y |
|
2 |
|
|
2 |
|
|
y y |
|
|
|
|
y |
2 |
|
2 |
|
||||||
( |
|
) |
|
d |
|
2 |
|
d d ( |
|
) |
|
d |
( |
|
) |
|
d |
|
2 |
|
d d |
( |
|
) |
|
d |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ed 2 |
|
2 fd d gd 2 |
|
|
(19) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
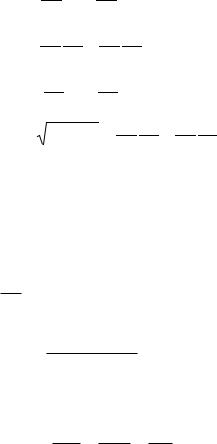
де e, f, g, h – відомі в картографії коефіцієнти Гаусса, вирази яких мають вигляд:
|
|
|
( |
|
x |
)2 |
( |
|
y |
) |
2 |
|
|
|
|
||||
e |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
x |
|
|
|
y |
|
y |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
g |
( |
) |
2 |
( |
) |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y |
|
y |
x |
||
h |
|
|
|
eg |
f |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Підставивши (19) у формулу масштабу, отримаємо : |
|
|
|
|
|||||||||||||||
2 |
|
ed 2 |
2 fd d gd 2 |
(20) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
M 2d 2 r 2d 2 |
|
|
|
|
||||||||
Введемо додаткову функцію:
u
d d
і поділимо чисельник та знаменник (20) на dλ2, отримаємо :
|
|
|
eu |
2 |
2 fu g |
|
||||
|
2 |
|
|
(21) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
2 |
u |
2 |
r |
2 |
|
|
|
|
|
|
|
|
|
||||
Знайдемо значення u з трикутника (рис.1):
tg |
dS |
n |
|
rd |
|
r |
|
|
|
||||
|
|
|
|
|
|
|
|
dS |
m |
|
md |
|
Mu |
|
|
|
|
|
|
звідки
u |
r |
ctg |
(23) |
|
M |
||||
|
|
|
(22),
Підставивши значення u у формулу (21) отримаємо :
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
r |
ctg 2 2 f |
r |
|
ctg g |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
e |
|
|
f |
|
g |
|
|
||||||||||
|
2 |
|
|
M |
|
M |
|
|
|
|
|
|
|
|
2 |
2 |
cos sin |
2 |
(24) |
|||||
|
|
|
|
|
|
|
|
|
|
cos |
|
|
sin |
|||||||||||
|
|
|
r 2 (ctg 1) |
|
|
|
|
|
M 2 |
|
Mr |
r 2 |
|
|||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
M |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Введемо позначення : Q |
|
|
|
|
|
(25) |
|
|
|
|
|
|
|
|
|
|||||||||
Mr |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В результаті отримаємо загальну формулу масштабу довжин:
2 P cos2 Q sin 2 R sin2 |
(26) |
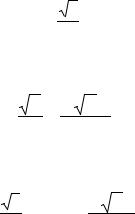
При α = 0˚ (180˚) μ2 = m2 = Р, а отже масштаб вздовж
m |
e |
|
M |
||
|
меридіанів:
(27)
При α = 90˚ (270˚) μ2 = n2 = R, а отже масштаб вздовж паралелей:
n |
g |
|
g |
|
r |
N cos |
|||
|
|
(28)
Відповідно для поверхні кулі, де M=N=R – радіус кулі, будемо мати:
m |
e |
, |
n |
g |
|
R |
R cos |
||||
|
|
|
(29)
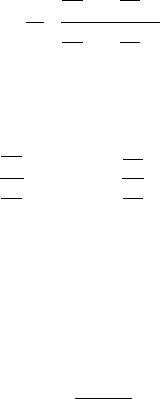
4. Зображення азимута в проекції. Кут між меридіанами та паралелями. Умова ортогональності сітки.
Розглянемо зображення елементарної сфероїдної трапеції на площині (рис.2).
Кут β – азимут довільного напрямку на площині (в проекції), α – на еліпсоїді;
Кут і – між меридіаном і паралеллю;
γm – кут між меридіаном точки А і віссю Х;
γn – кут між віссю Х і паралеллю точки А;
ψ – кут між віссю Х і dS′.
Знайдемо кути ψ, γm, γn (з рис.2.)
Для визначення β побудуємо на площині зображення елементарної сфероїдної трапеції (рис
2).
|
|
|
|
y |
d |
y |
d |
|
|
dy |
|
|
|
||
tg |
|
|
|
(30) |
|||
dx |
x |
|
x |
||||
|
|
|
d |
d |
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
Приймаючи λ=const для меридіана, φ=const для паралелі, знайдемо кути перетину меридіана та паралелі з віссю Х:
|
|
|
y |
|
|
|
y |
|
tg |
|
|
|
tg |
|
|
|
|
m |
x |
n |
x |
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
(31)
Знайдемо азимут β елементарного відрізку dS′: |
|
|
|
β=ψ-γm, (32) або |
tg |
tg tg m |
(33) |
|
|||
|
|
1 tg tg m |
|
Підставивши в останню формулу (33) вирази tgψ та tgγm з використанням коефіцієнтів Гаусса отримаємо після нескладних перетворень:
tg |
hd |
|
ed fd |
||
|
,
а після введення додаткової функції u |
d |
: |
|||
|
|||||
|
|
|
|
||
tg |
h |
|
(34) |
||
|
|
||||
eu f |
|
||||
Підставивши у формулу (34) значення u з формули (23)
u |
r |
|
M |
||
|
ctg
, отримаємо:
tg |
Mh |
або |
tg |
Mhtg |
(35) |
|
erctg Mf |
er Mftg |
|||||
|
|
|
|
На підставі (рис 2) отримаємо формули для кута і між зображеннями меридіанів та паралелей проекції: і = γn - γm , або:
|
|
|
|
|
|
|
|
y |
|
y |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
x |
|
x |
y |
|
x |
y |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
tg |
|
tg |
|
|
|
|
|
|
|
|
|||||||
tgi |
n |
m |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 tg |
n |
tg |
m |
|
|
y |
|
y |
|
x |
x |
|
y |
y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
з позначеннями коефіцієнтів Гауса
tgi |
h |
|
f |
||
|
(36)
Щоб картографічна сітка була ортогональна кут і = 90˚, а це можливо коли f = 0
f |
x x |
|
y y |
0 |
(37) |
|||||
|
|
|
|
|
|
|||||
|
|
|||||||||
|
|
|
|
|||||||
це умова ортогональності картографічної сітки.
Замість кута і в математичній картографії як правило використовують кут ε, який показує відхилення кута і від 90˚, тобто характеризує неортогональність сітки
ε = і – 90˚ |
|
|
|||
Оскільки tgi tg(90 ) |
h |
, звідки : |
tg |
f |
|
f |
h |
||||
|
|
|
|||
Таким чином можна зробити висновок, що є два взаємно перпендикулярних напрями на поверхні картографування, які залишаються взаємно перпендикулярними і в проекції (на карті). Ці напрями називаються головними, а масштаби вздовж цих напрямів екстремальними. У випадку, коли картографічна сітка є ортогональною головні напрями співпадають з меридіанами і паралелями.
5. Еліпс спотворень. Екстремальні масштаби (максимальний і мінімальний масштаби довжин. Формули зв’язку екстремальних масштабів з масштабами вздовж меридіанів і паралелей.)
