
scherbo-sp1
.pdf
площадки прямоугольную полоску шириной b и высотой dy (см. рис. 6.4), найдем
|
h b |
|
|
bh |
|
||
J x1y1 = ∫ y1x1dF = ∫ |
|
y1bdy1 |
=F |
|
. |
||
2 |
2 2 |
||||||
F |
0 |
|
|
|
|||
Треугольник. Вычислим момент инерции относительно центральной оси Ох. Ширина элементарной площадки, заштрихованной на рис. 6.5, определится из подобия треугольников:
by = |
b |
2 |
|
|
|
h − y . |
|
|
h 3 |
|
|
Подстановка этого выражения в интеграл дает
|
|
|
2 |
h |
|
b 2 |
|
b |
|
2 |
h |
|
2 |
|
|
|
|
|
bh3 |
|
|||||
|
2 |
|
3 |
2 |
|
|
3 |
|
|
2 |
|
3 |
|
|
|||||||||||
J x = ∫ y |
|
dF = |
∫ y |
|
|
|
|
h − y dy = |
|
|
∫ |
|
|
hy |
|
− y |
|
dy = |
|
. |
|||||
|
|
|
|
h |
3 |
|
|
36 |
|||||||||||||||||
F |
|
|
− |
h |
|
h 3 |
|
− |
h |
|
|
|
|
|
|
|
|||||||||
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем теперь момент инерции относительно оси симметрии Оy. Ширина bx элементарной полоски найдется из подобия треугольников:
bx = h b − x ,b 22
следовательно,
|
|
|
|
|
b |
|
|
|
|
|
|
|
b x3 |
|
x4 |
|
|
hb3 |
|
||
|
2 |
|
2h |
2 |
b |
|
2 |
|
2h |
|
|
|
|
||||||||
J y = ∫x |
|
dF = 2 |
|
|
∫ |
|
|
− x x |
|
dx = 2 |
|
|
|
|
|
− |
|
|
= |
|
. |
|
b |
|
|
b |
|
2 3 |
4 |
48 |
|||||||||||||
F |
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|||||||||
Круг. Для круга удобнее всего вычислить сначала полярный момент инерции и затем через него определить моменты инерции относительно центральных осей. На рис. 6.6 показана элементарная площадка, вырезанная двумя радиусами и двумя параллельными окружностями,
dF = ρdϕdρ.
Интегрирование по всей площади заменяется двойным интегрированием:
|
|
ρ2dF = |
|
ρ2ρdϕdρ = |
2π |
R |
ρ2dρ = |
R |
4 2π |
πR |
4 |
|||
Jρ = |
∫ |
∫∫ |
∫ |
dϕ |
∫ |
|
∫ |
dϕ = |
. |
|||||
|
|
|
|
|
4 |
|
2 |
|
||||||
|
F |
|
F |
|
0 |
|
0 |
|
|
|
0 |
|
|
|
Учитывая, что полярный момент инерции равен сумме двух осевых моментов, получим
J x = J y = J2ρ = πR4 4 .
81
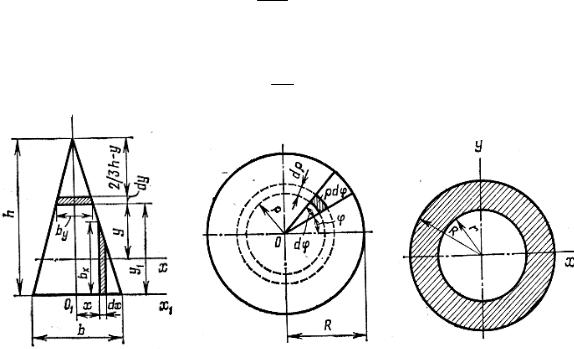
Кольцо. Момент инерции кольца (рис. 6.7) может быть найден как разность моментов инерции двух кругов: наружного и внутреннего. Полярный момент инерции равен
Jρ = πR2 4 − π2r 4 = π2 (R4 − r 4 ),
и осевые моменты инерции определяют по формуле
J x = J y = J4ρ (R4 − r4 ).
Рис. 6.5 |
Рис. 6.6 |
Рис. 6.7 |
6.3. Зависимость между моментами инерции относительно параллельных осей
Предположим, что моменты инерции относительно осей Ох и Оу, а также площадь фигуры заданы. Определим моменты инерции относительно новых осей О1х1 и О1у1, параллельных заданным.
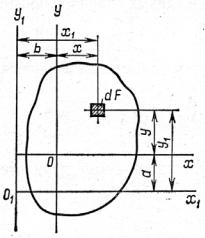
Из рис. 6.8 можно установить зависимость между координатами:
y1 = y + a, x1 = x + b.
Пользуясь общей формулой для осевых моментов инерции, найдем
J x1 = ∫ y12dF =∫( y + a)2 = ∫ y2dF +
F F F
+ 2a ∫ ydF + a2 ∫dF = J x + 2aSx + a2 F.
F F
Таким же путем можно установить, что
J y1 = J y + 2bS y + b2 F.
82
Для центробежного момента инерции имеем
J y x |
= ∫ y1x1dF =∫( y + a)(x + b)dF = |
||
1 |
1 |
F |
|
|
|
F |
|
= ∫xydF + ab ∫dF + a ∫xdF + b ∫ ydF = J xy + abF + aS y + bSx .
F F F F
В этих формулах Sx и Sy представляют собой статические моменты фигуры относительно осей Ох и Оу. Если эти оси центральные, то статические моменты относительно них равны нулю (Sx = 0, Sy = 0). Тогда формулы для моментов инерции относительно осей, параллельных центральным, примут следующий вид:
J x |
= J x + a2 F, |
|
|
1 |
= J y +b2 F, |
|
|
J y1 |
|
(6.2) |
|
J x y |
= J xy + abF. |
Рис. 6.8 |
|
1 1 |
|
|
|
Формулы (6.2) часто применяют для вычисления моментов инерции сложных фигур.
Складывая две первые строчки равенств (6.2) и учитывая, что Jρ1 = Jρ + (a2 +b2 )F получим формулу для полярного момента инерции
Jρ1 = Jρ + (a2 + b2 )F.
Если заданными являются моменты инерции относительно произвольных осей, то для центральных осей, параллельных данным осям, путем решения уравнений (6.2) относительно Jx, Jy и Jxy получим следующие формулы:
J x = J x + a2 F, |
|
|
1 |
|
|
J y = J y1 +b2 F, |
|
(6.3) |
J xy = J x y + abF. |
|
|
1 1 |
|
|
Из этих формул видно, что моменты инерции относительно центральных осей имеют наименьшие значения по сравнению с моментами инерции относительно любых других параллельных осей.
Пример.
Определить момент инерции прямоугольника относительно основания, если момент инерции относительно центральных осей задан.
83
Применяя формулы (6.2), находим
J x |
= J x + a2 F = |
bh2 |
h |
2 |
bh3 |
. |
|
12 |
+ |
bh = |
3 |
||||
1 |
|
|
2 |
|
|
||
Этот же результат был получен ранее путем интегрирования.
6.4. Зависимость между моментами инерции при повороте осей. Главные оси и главные моменты инерции
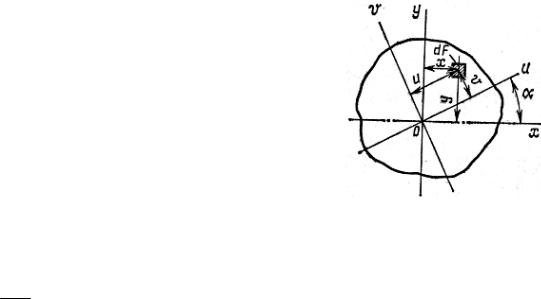
Пусть моменты инерции относительно осей Ох и Оу заданы. Найдем моменты инерции для осей Оu и Оv, повернутых относительно исходной системы осей на угол α (рис. 6.9).
Выберем произвольную площадку dF и выразим ее координаты в новых осях через координаты в старых осях:
v = y cos α − xsin α, u = y sin α + x cos α.
Найдем момент инерции относительно оси Ои:
Ju = ∫v2dF = ∫( y cos α − xsin α)2 dF =
FF
=cos2 α∫ y2dF +sin2 α∫x2dF − 2sin αcos α∫ yxdF.
|
|
F |
|
|
F |
|
|
F |
|
|
Учтя, что |
|
|
|
|
|
|
|
|
|
|
∫ y2dF = J x , |
∫x2dF = J y , |
∫xydF = J xy , |
|
|||||||
F |
|
|
|
F |
|
|
|
F |
|
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
Ju = J x cos2 α + J y sin2 α − J xy sin 2α. |
|
(6.4) |
||||||
Точно таким же образом можно установить, что |
|
|
||||||||
|
|
Jv = J x sin2 α + J y cos2 α − J xy sin 2α. |
|
(6.5) |
||||||
Для центробежного момента инерции имеем |
|
|
|
|||||||
Juv = ∫( y cos α − xsin α)( y sin α + x cos α)dF = |
|
|
||||||||
F |
|
|
|
|
|
|
x2dF + (cos2 α −sin2 |
α) |
|
|
= sin αcos α |
∫ |
y2dF −sin αcos α |
∫ |
xydF, |
||||||
|
|
|
|
|
|
|
∫ |
|
||
|
F |
|
|
|
|
F |
|
|
F |
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
Juv = |
J x − J y |
sin 2α + J xy cos 2α. |
|
(6.6) |
||||
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
84 |
|
|
|
|
|
Таким образом, зная моменты инерции относительно двух взаимно перпендикулярных осей и центробежный момент инерции относительно этих осей, можно найти момент инерции относительно любой оси, проходящей через ту же точку.
Интересно отметить, что если сложить выражения (6.4) и (6,5), то получим уже известное соотношение
Ju + Jv = J x + J y .
Из формулы (6.4) видно, что величина момента инерции относительно произвольной оси зависит от угла наклона оси α. Очевидно, можно найти такое значение угла α0, при котором момент инерции достигает экстремального значения. Для определения экстремума приравняем
нулю первую производную от выражения (6.4) Рис. 6.9 и положим α = α0 :
dJdαu = −2J x cos α0 sin α0 + 2J y sin α0 cos α0 − 2J xy cos 2α0 = 0,
или
(J x − J y )sin 2α0 + 2J xy cos 2α0 = 0,
откуда
tg2α0 |
= − |
2J xy |
. |
(6.7) |
||
J x |
− J y |
|||||
|
|
|
|
|||
Полученная формула дает для угла α0 два значения: α'0 и α0"=α'0+90°, следовательно, существуют две взаимно перпендикулярные оси, относительно которых моменты инерции имеют экстремальные значения. Такие оси называют главными осями инерции, а моменты инерции относительно этих осей – главными моментами инерции.
Подробные исследования показывают, что относительно одной из главных осей инерции момент инерции принимает максимальное значение,
а относительно другой – минимальное. Сравнивая выражения σα (3.3) и Ju
(6.4), а также τα (3.4) и Juv (6.6), а затем формулы (6.7) и (3.12), можно за-
метить, что задаче отыскания главных моментов инерции математически тождественна задача отыскания главных напряжений. На основании этого не будем повторять все выводы, а ограничимся лишь приведением окончательных результатов.
Выражения для главных моментов инерции записываются по аналогии с формулами (3.13), полученными в п. 3.4 для главных напряжений:
85
Jmax = |
J x + J y |
+ |
1 |
(J x − J y )2 |
+ 4J xy2 , |
(6.8) |
|
2 |
2 |
||||||
|
|
|
|
|
|||
Jmin = |
J x + J y |
− |
1 |
(J x − J y )2 |
+ 4J xy2 . |
|
|
2 |
2 |
|
|||||
|
|
|
|
|
Из формулы (6.8) видно, что величины главных моментов инерции определяются непосредственно через моменты инерции относительно осей Ох и Оу. Поэтому их можно определить, не зная положения самих главных осей.
Оказывается, что положение главных осей помимо формулы (6.7) можно найти и через моменты инерции Jmax и Jmin.
Приведем без вывода формулы, позволяющие найти углы α1 и α2 между осью Ох и главными осями:
tgα1 = |
J xy |
; |
tgα2 = |
J xy |
. |
||
J y − Jmax |
J y − Jmin |
||||||
|
|
|
|
||||
Угол α1 определяет положение оси, относительно которой момент |
|||||||
инерции равен Jmax, а угол α2 |
– Jmin. |
|
|
|
|||
При исследовании напряженного состояния в точке было показано, что касательные напряжения на главных площадках равны нулю. Точно так же здесь можно показать, что центробежный момент инерции относительно главных осей инерции равен нулю. Это обстоятельство легко доказать, если в формулу (6.6) вместо угла α подставить значение α0, определяемого формулой (6.7).
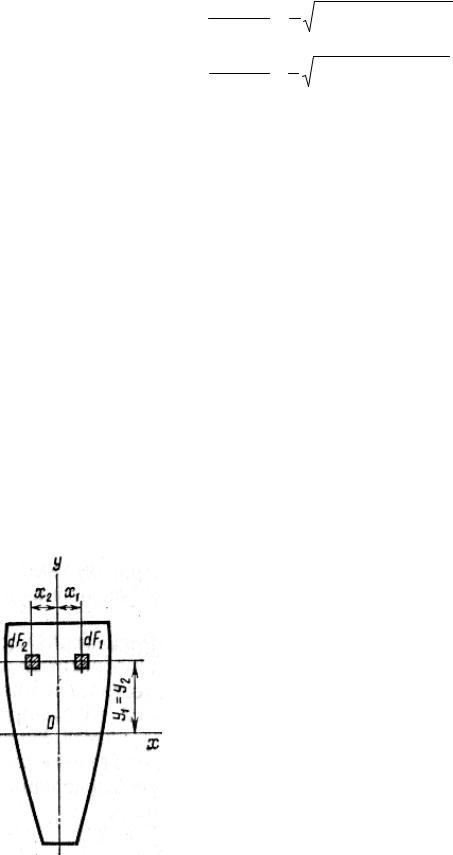
Условие равенства нулю центробежного момента инерции часто используют для определения положения главных осей инерции. Так, например, для симметричной фигуры ось симметрии является главной осью. В самом деле, разделяя симметричную фигуру (рис. 6.10) на две половины и вычисляя элементарный момент инерции двух одинаковых симметрично расположенных элементарных площадок в точках, равноотстоящих от оси симметрии Оу, получим:
– для правой точки
|
dJ xy = dF1x1 y1; |
|
– для левой точки |
|
dJ xy = dF2 x2 y2 , |
|
но так как dF1 = dF2, а в силу симметрии х2 = - х1; |
|
у2 = у1, то сумма двух элементарных моментов |
Рис. 6.10 |
инерции равна нулю, поэтому и для всего сечения |
|
86 |
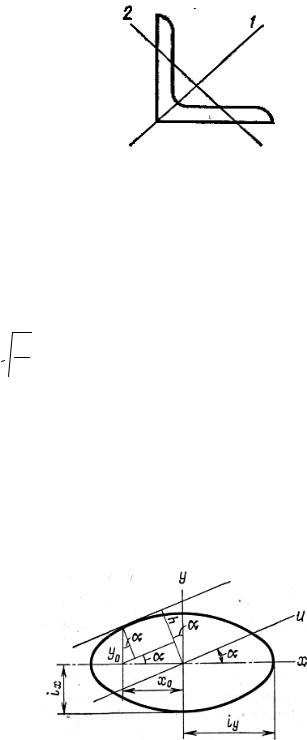
момент инерции Jxy равен нулю. Таким образом, для всех симметричных фигур главные оси устанавливаются без вычислений. Одна ось совмещается с осью симметрии, а другая проводится перпендикулярно ей. Особое значение имеют главные оси, которые проходят через центр тяжести. Такие оси называются главными центральными осями. На рис. 6.11 показаны главные центральные оси для равнобокого уголка. Одна из главных осей совпа-
дает с биссектрисой, так как последняя является осью симметрии. Вторая главная ось перпендикулярна первой и проходит через центр тяжести.
6.5. Эллипс инерции и его свойства
Введем новую геометрическую характеристику, которую назовем радиусом инерции:
i =  FJ .
FJ .
Предположим, что для какой-либо фигуры оси Оу и Ох являются главными центральными осями. Напишем выражение момента инерции относительно оси, наклоненной по отношению к главным осям на угол α:
Ju = J x cos2 α + J y sin 2 α.
Разделив все слагаемые на F, получим
iu2 = ix2 cos2 α +iy2 sin 2 α.
Построим в осях координат эллипс, взяв за полуоси радиусы инерции фигуры (рис. 6.12). При этом вдоль оси Ох отложим радиус iy, а на оси Оу – соответственно радиус инерции ix. Запишем уравнение этого эллипса:
y2 |
+ |
x2 |
=1. |
(6.10) |
|
ix2 |
iy2 |
||||
|
|
|
(6.9)
О
Рис. 6.12
Данный эллипс называется эллипсом инерции фигуры. Проведем касательную к эллипсу параллельно оси Ои (у0 и х0 – координаты точки касания) и напишем уравнение этой касательной:
yy0 |
+ |
xx0 |
=1. |
(6.11) |
|
ix2 |
iy2 |
||||
|
|
|
|||
|
87 |
|
|
||
Далее найдем расстояние между касательной и осью Ои. Из чертежа видно, что
h = y0 cos α + x0 sin α.
Разделив все члены на h, получим
|
|
|
|
|
|
y0 cos α |
+ |
x0 sin α |
=1. |
|
|
(6.12) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
h |
|
|
|
h |
|
|
|
|
|
|
|
|||
Сравнивая уравнения (6.11) и (6.12), можно сделать заключение, что |
|||||||||||||||||||||
|
|
|
|
y |
= cos α |
; |
|
|
x |
|
= sin α |
, |
|
|
|||||||
|
|
|
ix2 |
h |
|
|
|
iy2 |
|
|
|
h |
|
|
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iy2 sin |
2 α |
|
|||
|
y2 |
|
|
|
|
i2 cos2 α |
|
|
|
x2 |
|
|
|
||||||||
|
|
= |
|
|
x |
; |
|
|
|
|
= |
|
|
|
|
. |
|||||
|
ix2 |
|
|
h2 |
|
|
iy2 |
|
h |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Если теперь подставить в уравнение эллипса инерции полученные |
|||||||||||||||||||||
величины, то будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ix2 cos2 α |
+ |
|
iy2 sin |
2 α |
=1, |
|
|
|
||||||||
|
|
|
|
|
|
|
h2 |
|
|
|
h2 |
|
|
|
|
|
|
||||
откуда
h2 = ix2 cos2 α +iy2 sin 2 α.
Сравнивая полученную зависимость с выражением (6.9), видим, что величина h численно равна радиусу инерции относительно наклонной оси. Установленное свойство эллипса инерции позволяет графически определить момент инерции относительно любой оси, проходящей через начало координат. Для этого достаточно провести касательную к эллипсу параллельно этой оси и замерить кратчайшее расстояние между касательной и осью. Это расстояние h и будет равно радиусу инерции для рассматриваемой оси. Момент инерции определится с помощью равенства
Ju = h2 F.
Если моменты инерции относительно двух главных осей равны между собой, то эллипс инерции обратится в круг. Это свидетельствует о том, что моменты инерции относительно всех осей, проходящих через центр тяжести, равны между собой.
Для таких сечений все оси являются главными осями. К числу таких сечений относятся круг, кольцо, квадрат и т. п.
88
6.6. Вычисление моментов инерции сложных фигур
При расчете различных балок приходится определять моменты инерции сложных поперечных сечений. Для практических расчетов следует разбить сложную фигуру на простейшие и для каждой из них вычислить момент инерции относительно рассматриваемой оси. Расчет начинается с определения центра тяжести всей фигуры по отношению к произвольной системе координат.
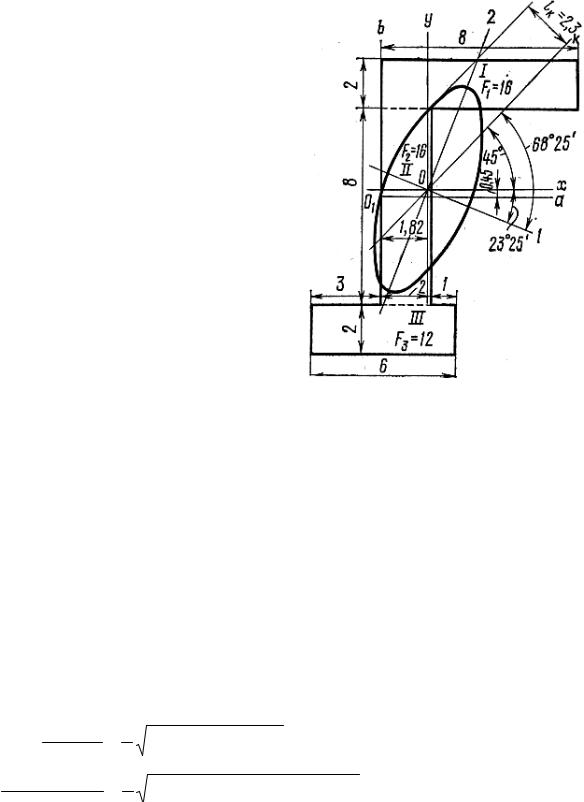
Рассмотрим пример определения моментов инерции для фигуры, показанной на рис. 6.13. В качестве начальных осей возьмем оси O1а и O1b. Разобьем фигуру на три прямоугольника: I, II, III.
Найдемположениецентратяжести:
a0 = 16 4 +16 1 =1,82 см; 16 +16 +12
b0 = 16 4 +16 1 =1,82 см. 16 +16 +12
|
|
Находим моменты инерции от- |
|
|
|
|
Рис. 6.13 |
|
|
||||||||||
носительно осей, проходящих через |
|
|
|
|
|
|
|
|
|
||||||||||
центр тяжести, применяя формулы перехода (6.2): |
|
|
|
|
|
||||||||||||||
J |
|
|
8 23 |
+ 4,552 |
16 |
|
+ |
|
2 83 |
+ 0,452 |
16 |
|
|
6 22 |
+ 5,452 |
|
|
= 785,6 см4 |
; |
x |
= |
|
|
|
|
|
+ |
|
12 |
||||||||||
|
|
12 |
|
|
|
|
|
12 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
J |
|
|
2 83 |
+ 2,182 |
16 |
|
+ |
|
8 23 |
+ 0,822 |
16 |
|
|
2 63 |
+1,822 12 |
|
|
|
|
y |
= |
|
|
|
|
|
+ |
|
= 253,2 см4 . |
|
|||||||||
|
|
12 |
|
|
|
|
|
12 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Находим центробежный момент инерции относительно центральных
осей:
J xy = 4,55 2,18 16 + (−0,82)(−0,45) 16 + (−5,45)(−1,82) 12 = 283,6 см4 .
Главные моменты инерции найдем по формулам (6.8):
Jmax = |
J x + J y |
+ |
1 |
(J x − J y )2 + 4J xy2 = |
|
|
2 |
2 |
|
||||
|
|
|
|
|
||
= |
785,6 + 253,2 |
+ |
1 |
(785,6 − 253,2)2 + 4 |
283,62 = 519,4 +388,8 = 908,2 см4 . |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
89 |
|
Jmin = 519,4 −388,8 =130,6 cм4 .
Для определения угла наклона главных осей по формуле (6.7) находим
tg2α0 = − |
2 283,6 |
= −1,065, |
|
785,6 − 253,2 |
|||
|
|
следовательно,
2α0 = −46 |
o |
′ |
|
o |
′ |
50 , |
α0 = −23 25 . |
||||
Угол α0 дает положение главной оси, относительно которой момент |
|||||
инерции имеет максимальное значение при J x |
> J y и минимальное – при |
||||
J x < J y . Главные центральные оси инерции – 1 и 2. Найдем радиусы инерции:
imax = |
908,2 |
= 4,54 cм; |
imin = |
130,6 |
=1,72 см. |
|
44 |
|
|
44 |
|
По этим данным построен эллипс инерции (см. рис. 6.13).
Найдем по эллипсу момент инерции относительно оси, наклоненной к горизонту под углом 45°. Эта ось по отношению к главной оси наклонена под углом 68° 25′. Параллельно этой оси проведена касательная к эллипсу. Расстояние от оси 1 до касательной lк≈ h = 2,3 см. Следовательно, на основе графического решения искомый момент инерции равен
Jк = h2 F = 2,32 44 = 232,8 cм4 .
Найдем этот же момент инерции аналитическим путем. Для этого воспользуемся формулой (6.4), только запишем ее, принимая за исходные главные моменты инерции. В этом случае формула не будет содержать третье слагаемое, так как центробежный момент инерции относительно главных осей равен
Jк = Jmax cos2 α + Jmin sin 2 α = 908,2 cos 68o25′+130,6sin 68o25′ = = 908,2 0,3682 +130,6 0,932 = 235,6 cм4 .
Результаты графического и аналитического решений близки друг другу.
90
