scherbo-sp1

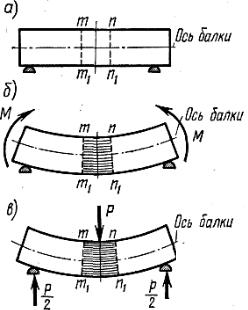
М-7. ИЗГИБ ПРЯМЫХ СТЕРЖНЕЙ

7.0. Введение в модуль

Модуль содержит следующие структурные элементы:

1.Общие замечания об изгибе балок.

2.Основные типы балок и опорных связей.

3.Внутренние силы при изгибе.

4.Построение эпюр моментов и поперечных сил в балках.

5.Чистый изгиб. Определение нормальных напряжений.

6.Касательные напряжения при изгибе.

7.Анализ напряженного состояния при изгибе.

8.Проверка прочности балок при изгибе.

9.Расчет составных балок.

10.Определение разрушающих нагрузок при изгибе балок за пределом упругости.

7.1.Общие замечания об изгибе балок

Встроительных конструкциях в большом количестве встречаются элементы, работающие на изгиб. Стержни, работающие преимущественно на изгиб, принято называть балками. На рис. 7.1, а показана балка в естественном состоянии (без нагрузки), а на рис. 7.1, б изображена та же система, изогнутая двумя парами, приложенными по концам.

Если на боковой поверхности балки изобразить прямоугольник mnn1m1 то, как показывают эксперименты, после деформации этот прямоугольник превратится в фигуру, близкую к трапеции, с дву-

мя прямолинейными сторонами mm1 и nn1 и двумя криволинейными сторонами mn и

m1n1, как это показано на рис. 7.1, б. Нижние волокна при этом удлинятся, а верхние укоротятся. Таким образом, при изгибе часть волокон, расположенных по высоте балки, испытывает растяжение, а часть – сжатие. Ось и продольные волокна при изгибе балки искривляются. Аналогичная картина происходит при изгибе силой Р, как показано на рис. 7.1, б, или вообще при действии системы сил, приложенных к балке перпендикулярно оси, а также пар сил, лежащих в плоскостях,

91

Взависимости от способов приложения нагрузки и способов закрепления стержня могут возникать различные виды изгиба. В случае, когда изгибающий момент в поперечном сечении балки является единственным силовым фактором, а все остальные равны нулю, изгиб называется чистым. Такой случай показан на рис. 7.1, б. Изучение напряжений и деформаций в балках при изгибе обычно начинают с наиболее простого случая чистого изгиба.

Если наряду с изгибающим моментом в поперечных сечениях возникают также и поперечные силы, а нормальная сила при этом равна нулю, то имеем так называемый поперечный изгиб (рис. 7.1, в).

Встроительной практике очень часто встречаются балки, поперечное сечение которых имеет хотя бы одну ось симметрии. Если все силы, в том числе и опорные реакции, лежат в плоскости, совпадающей с осью симметрии сечения, то ось изогнутой балки также лежит в этой плоскости. Такой изгиб называют плоским.

Внастоящей главе главным образом рассматривается плоский изгиб.

7.2. Основные типы балок и опорных связей

Для того чтобы балка могла воспринимать нагрузку и передавать ее на основание, она должна быть соединена с ним опорными связями. На практике применяют несколько типов опорных связей, или, как говорят, несколько типов опор. Опорные реакции зависят от устройства опоры. Различают три основных типа опор.

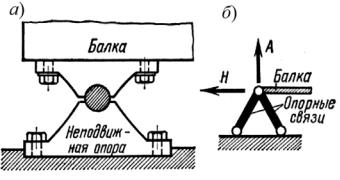
1. Шарнирно-неподвижная опора (рис. 7.2, а). Эта опора допускает свободный поворот сечения балки над опорой в одной плоскости относительно оси цилиндрического шарнира, но не дает возможности смещаться ни по вертикали, ни по горизонтали. Схематически шарнирно-непо- движная опора изображается в виде двух стерженьков, шарнирно соединенных с балкой (рис. 7.2, б). Подразумевается, что шарнир не оказывает сопротивления вращению примыкающего к нему сечения балки. В такой опоре возникают две составляющие опорной реакции: А и Н.

Рис. 7.2

92

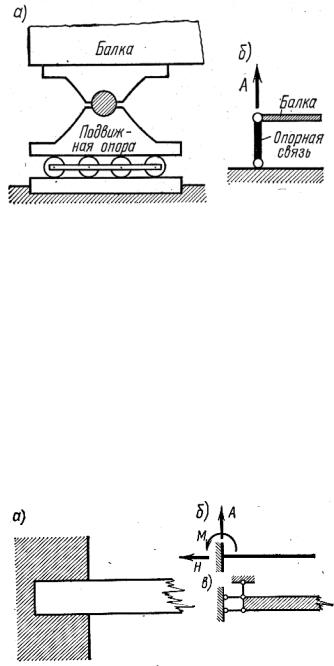
2. Шарнирно-подвижная опора (рис. 7.3, а). Эта опора допускает пе-

ремещение в одном направлении, например, по горизонтали, и поворот сечения – над опорой вокруг шарнира. Схематическое изображение шарнирноподвижной опоры показано на рис. 7.3, б. Реакция такой опоры А направлена вдоль опорной связи или перпендикулярно плоскости опирания катков.

Рис. 7.3

3. Заделка (рис. 7.4, а). Такая опора не допускает поворота и перемещения по двум направлениям сечения балки, примыкающего к заделке. Схематически заделка изображается так, как показано на рис. 7.4, б. Реакции в заделке состоят из вертикальной силы А, горизонтальной силы Н и момента М. Иногда заделку представляют в виде трех линейных связей, показанных на рис. 7.4, в. Усилия, возникающие в трех связях, и создают реакции А, Н и М.

Таким образом, заделка изображается в двух вариантах, как показано на рис. 7.4, б, в. Из второго варианта видно, что заделка балки равносильна закреплению ее тремя связями в виде стержней.

Рис. 7.4

Для того чтобы балка могла воспринимать нагрузку, расположенную в одной плоскости, ее необходимо закрепить в этой плоскости с помощью

93

описанных выше связей. Наименьшее число связей, обеспечивающее неподвижность балки по отношению к основанию в одной плоскости, равно трем.

Применяют различные варианты прикрепления балки к основанию с помощью рассмотренных выше опор: например, достаточно балку заделать одним концом или закрепить с помощью двух опор (подвижной и неподвижной). Возможен случай прикрепления с помощью трех подвижных опор, однако при этом нельзя допускать, чтобы три опорных стержня были параллельны друг другу или пересекались в одной точке.

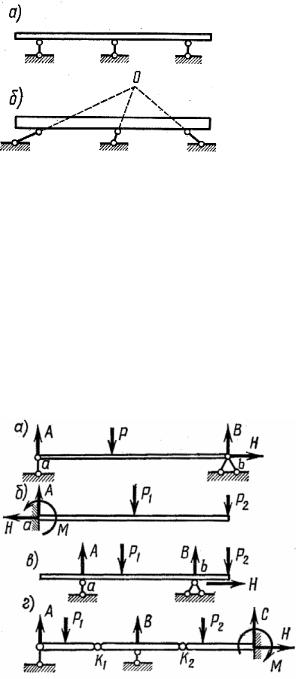
В случае, когда все три опорных стержня параллельны друг другу, балка может перемещаться по линии, перпендикулярной направлению стержней (рис. 7.5, а), поэтому такой случай прикрепления недопустим. В том случае, когда направления трех опорных стержней пересекаются в одной точке (рис. 7.5, б), балка может повернуться на малый угол вокруг точки О, что также недопустимо.

На рис. 7.6 показаны различные типы балок в зависимости от способов прикрепления их к основанию:

1)простая двухопорная балка (рис. 7.6, а), у которой одна опора подвижная, а другая неподвижная;

2)балка, заделанная одним концом (рис. 7.6, б);

3)балка с консолями (рис. 7.6, в).

Встречаются также более сложные типы балок, представляющие собой систему брусьев, соединенных между собой связями.

На рис. 7.6, г показана сложная система, состоящая из трех брусьев, соединенных шарнирами в точках К1 и К2. В этой системе число опорных связей равно пяти.

Для расчета балки на изгиб необходимо знать все действующие на нее силы. Поскольку внешняя нагрузка обычно бывает задана, то для вычисления всех действующих на балку сил приходится определять неизвестные опорные реакции. Эта задача подробно изучалась в курсе теоретической механики. Напомним вкратце методы определе-

94

ния реакций. Уравнения равновесия тела, загруженного плоской системой сил, могут быть записаны в трех формах:

1) ∑Z = 0; ∑Y = 0; ∑mO = 0;

здесь сумма моментов берется относительно любой точки О, лежащей в плоскости действия сил;

2) ∑ma = 0; ∑mb = 0; ∑Z = 0;

в этом варианте ось Оz не должна быть перпендикулярна прямой ab; 3) ∑ma = 0; ∑mb = 0; ∑mc = 0;

применяя этот вариант, необходимо помнить, что точки a, b и с не должны лежать на одной прямой.

При определении опорных реакций необходимо стремиться так составить уравнения, чтобы в каждое из них входило только одно неизвестное. Этого можно добиться, составляя два уравнения моментов относительно опорных точек, как это рекомендуется вариантом 2. Тогда, определив реакции А и В, обычно производят проверку по уравнению

∑Y = 0.

Иначе говоря, сумма вертикальных реакций должна равняться сумме всех вертикальных внешних сил.

При расчете сложных балок, состоящих из нескольких брусьев,

следует иметь в виду, что уравнения равновесия можно применить как ко всей системе в целом, так и к каждому брусу в отдельности. В таких задачах общее число опорных реакций больше трех, но зато и независимых уравнений статики также больше трех. Так, например, для системы, изображенной на рис. 7.6, г, помимо трех уравнений статики для всей системы в целом, используются условия равенства нулю моментов относительно шарниров К1 и К2.

Системы, в которых число уравнений равновесия достаточно для определения всех опорных реакций, называют статически определимыми.

7.3. Внутренние силы при изгибе. Дифференциальные зависимости между М, Q и q

Наиболее распространенной нагрузкой являются параллельные силы, действующие на балку, лежащие в одной плоскости и пересекающие ось балки под прямым углом, а также пары сил, лежащие в той же плоскости.

Для того чтобы определить внутренние силовые факторы в произвольном поперечном сечении, необходимо мысленно рассечь балку на две части плоскостью, перпендикулярной оси балки, и рассмотреть равновесие одной из ее частей.

95

На рис. 7.7 показана балка, рассеченная плоскостью А0. Воздействие правой части, изображенной пунктиром, на левую заменено поперечной силой Qy и изгибающим моментом Мх. Легко доказать, что нормальная сила равна нулю. Для этого достаточно все силы, действующие на левую отсеченную часть балки, спроектировать на ось Оz, Все внеш-

ние силы проектируются на эту ось в нуль, следовательно, главный вектор внутренних сил также должен пересекать ось балки под прямым углом.

Таким образом, при поперечном изгибе во всех сечениях балки нор-

мальная сила равна нулю, внутренние силы сводятся к изгибающему моменту и поперечной силе.

Из рис. 7.8, а, где показана изогнутая балка, видно, что деформация изгиба сопровождается растяжением одних волокон и сжатием других. В рассматриваемом случае нижние волокна удлиняются, а верхние укорачиваются.

Установим для изгибающего момента и поперечной силы следующее правило знаков: изгибающий момент будем считать положительным, если он вызывает растяжение нижних волокон. Поперечную силу будем считать положительной, если она стремится повернуть вырезанный из

балки элемент бесконечно малой длины по ходу часовой стрелки.

На рис. 7.8, б показана балка, которая двумя сечениями, проведенными нормально к оси, разрезана на три части. Действие изгибающего момента и поперечной силы на эти три части показано в положительном направлении. Следует обратить особое внимание на правило знаков для поперечной силы, в особенности в связи с тем, что для левой отсеченной части балки положительная поперечная сила в рассматриваемом сечении направлена вниз, а для правой – вверх.

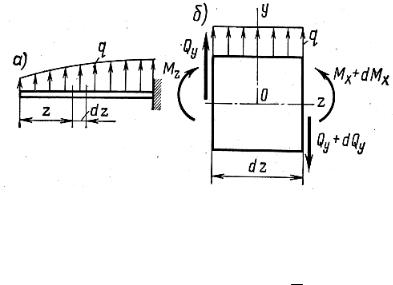
ной, если она направлена кверху; на протяжении длины dz ее считают равномерно распределенной.

Рис. 7.9

Составим два уравнения равновесия элемента:

∑mO = M x − (M x + dM x ) + Qy dz + 12 dQy dz = 0;

∑Y = qdz + Qy − (Qy + dQy ) = 0.

Впервом уравнении произведением dQydz как величиной второго порядка малости по сравнению с остальными слагаемыми можно пренебречь.

После элементарных преобразований из приведенных выше уравнений находим

Издвухполученныхдифференциальныхзависимостей вытекаеттретья:

Формулы (7.1), (7.2) и (7.3) будут использованы при анализе различных вопросов, связанных с изгибом балок. В частности, зависимостями (7.1) и (7.2) часто пользуются при проверке правильности построения эпюр моментов и поперечных сил.

7.4. Построение эпюр моментов и поперечных сил в балках

Для того чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента Мх и положение сечения, в котором он возникает. Точно так же надо знать наибольшую поперечную силу.

97

В отдельных случаях возникает необходимость получить значение моментов и поперечных сил в целом ряде точек. В связи с этим возникает необходимость выяснить закон изменения Мх и Qy по длине балки. Для этой цели обычно строят так называемые эпюры моментов и поперечных сил. Эти эпюры представляют собой графическое изображение функций Мх и Qy на протяжении всей балки. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы. Для построения этих эпюр определяют численное значение моментов и поперечных сил для ряда точек и по ним строят соответствующие графики.

Как указывалось в п. 7.3, при определении Мх и Qy в каком-либо сечении необходимо разрезать в этом сечении балку на две части и рассмотреть равновесие одной из отсеченных частей. Действие отброшенной части заменяется внутренними силовыми факторами Мх и Qy, которые и определяются из уравнений

равновесия.

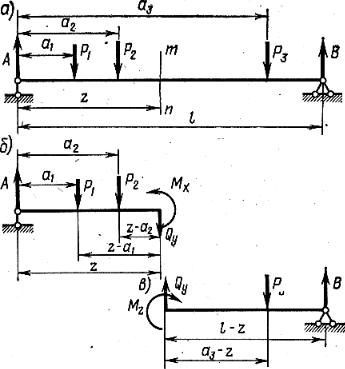
Так, для определения момента и поперечной силы в сечении m-n балки, показанной на рис. 7.10, а, разрезаем ее на две части. Левая отсеченная часть показана на рис. 7.10, б. Воздействие отброшенной правой части заменено моментом и силой, которые приложены в положительном направлении. На рис. 7.10, в показана правая часть с моментом и попереч-

ной силой, также приложенными в положительном направлении. Составляя уравнения равновесия для левой отсеченной части и счи-

тая при этом Qy и Мх как внешние силовые факторы

Здесь ∑Y л – сумма проекций всех внешних сил, приложенных к левой отсеченной части, на ось, перпендикулярную оси бруса; ∑mxл – сумма

моментов всех внешних сил, действующих на левую отсеченную часть, взятых относительно центра тяжести рассматриваемого сечения.

Рассматривая не левую, а правую часть, получаем:

На основании полученных формул легко определить значения Мх и Qy для любого сечения, а затем построить их эпюры. Следует обратить внимание на то, что формулы (7.4) и (7.5) отличаются от формул (7.6) и (7.7) знаком, что необходимо учитывать при практических расчетах.

На эпюре Qy положительные ординаты откладывают вниз, а отрицательные – вверх. Положительные моменты откладываются вниз, так как эти моменты согласно установленному правилу вызывают растяжение нижних волокон. Рассмотрим несколько примеров, из которых можно усвоить технику построения эпюр моментов и поперечных сил.

Пример 1.

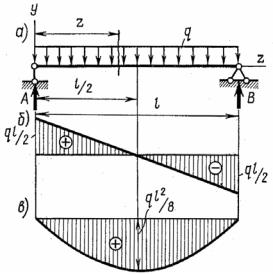
Построим эпюры Qy и Мх для балки на двух опорах с равномерно распределеннойнагрузкой(рис. 7.11, а).

Ввиду симметрии опорные реакции равны друг другу, а так как сумма реакций равна всей нагрузке, то

A = B = ql2 .

Поперечная сила в сечении z оп-

Получено уравнение прямой линии, которую можно построить по двум точкам, для этого необходимо вычислить два значения поперечной силы:

По этим ординатам построен график (рис. 7.11, б), который и представляет собой эпюру поперечных сил. Из эпюры видно, что в середине пролета поперечная сила равна нулю.

99

Изгибающий момент в произвольном сечении

По этому уравнению построена эпюра моментов, изображенная на рис. 7.11, в. Наибольшая ордината в середине пролета (при z = 2l ) равна

Там, где момент имеет максимальное значение, поперечная сила равна нулю. Это подтверждает также дифференциальная зависимость

dMdzx = Qy . Другое условие, dQdzy = q, также выполняется.

Из эпюры Qу видно, что тангенс угла наклона линии, изображающей эпюру Qy, постоянен по всей длине. Нагрузка q также постоянна по длине балки.

Пример 2.

Построить эпюры моментов и поперечных сил для балки с двумя консолями, загруженной, как показано на чертеже (рис. 7.12, а).

Рис. 7.12

100