
scherbo-sp1
.pdf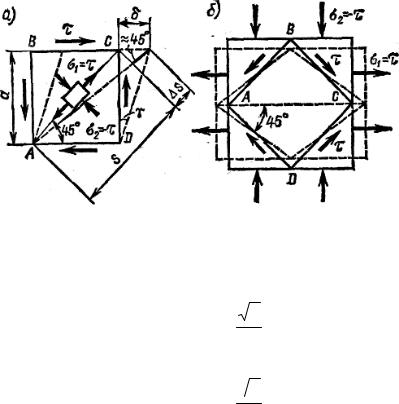
формации, показанной на рис. 4.7, а, получена путем растяжения и сжатия параллелепипеда главными напряжениями σ1 = −σ2.
Рис. 4.7
Удлинение диагонали АС вследствие деформации сдвига (см. рис. 4.7, а) равно
∆s = δcos 45o = |
2 aγ. |
|
2 |
Так как
a = s cos 45o =  22 s
22 s
и |
|
|
|
τ |
|
|
|
|
γ = |
, |
|
||||
|
G |
|
|||||
|
|
|
|
|
|
||
то |
|
|
|
τ |
|
|
|
|
∆s = |
|
s. |
(а) |
|||
|
2G |
||||||
|
|
|
|
|
|||
С другой стороны, применяя к волокну АС обобщенный закон Гука, |
|||||||
можно написать |
|
|
|
|
|
|
|
ε = ∆s |
= σ1 |
−µσ2 . |
|
||||
1 |
s |
|
|
E |
E |
|
|
|
|
|
|
||||
Подставляя σ1 = τ и σ2 = −τ, имеем |
|
||||||
|
∆s = |
(1 +µ)τ s. |
(б) |
||||
|
|
|
|
E |
|
|
|
Приравнивая выражения (а) и (б), получим искомое соотношение
G = |
E |
. |
(4.5) |
|
2(1 +µ) |
||||
|
|
|
||
|
61 |
|
|
Формула (4.5) показывает, что три постоянные Е, G и µ, характеризующие упругие свойства изотропного материала, связаны между собой. Найдя из опыта две из них, можно третью подсчитать по формуле (4.5). Например, для стали при Е = 2 106 кгс/см2 и коэффициенте Пуассона µ = 0,25 по формуле (4.5) найдем
G = |
2 106 |
= 8 105 кгс/см2 , |
|
2(1 + 0,25) |
|||
|
|
что соответствует значениям G, получаемым из эксперимента.
4.5. Потенциальная энергия при чистом сдвиге
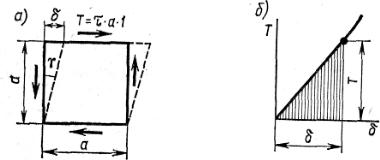
При деформации элемента, ограниченного площадками чистого сдвига, показанного на рис. 4.8, а, работу совершает только касательная сила Т, приложенная к его верхней грани на перемещении δ. Примем размер элемента, перпендикулярный чертежу, равным 1. Тогда эта сила равна T = τa 1. Сдвиг δ в пределах закона Гука пропорционален силе Т, что показано на рис. 4.8, б. Поэтому работа этой силы А и численно равная ей потенциальная энергия сдвига U, подсчитанные как заштрихованная площадь, определяются выражением
A =U = 12 Tδ,
или, учитывая, что Т = τа, а δ = γа, получим
U = 12 τγa2.
Рис. 4.8
Объем элемента V= а2 1, поэтому удельная потенциальная энергия деформации сдвига равна
u = U |
= |
1 |
τγ. |
(4.6) |
V |
|
2 |
|
|
|
62 |
|
|
|
Применяя закон Гука (4.3), окончательно найдем
u = |
1 |
τ2 |
. |
(4.7) |
|
2 |
G |
||||
|
|
|
Эта формула по записи напоминает аналогичную формулу для простого растяжения
u= 1 σ2 . 2 E
4.6.Практический расчет соединений, работающих на сдвиг
Ниже даются основные понятия о расчетах заклепочных (или болтовых) и сварных соединений.
Действительная их деформация весьма сложна и лишь приближенно может быть рассмотрена как деформация сдвига. Поэтому излагаемые здесь расчеты основаны на довольно грубых допущениях и во многом носят условный характер. Но исключительная простота расчетов обеспечила им широкое применение в практике проектирования. Кроме того, некоторые величины, используемые в расчетах, берутся на основании опытных данных, что вносит соответствующий корректив в расчеты и делает их достаточно надежными.
4.6.1. Расчет заклепочных и болтовых соединений
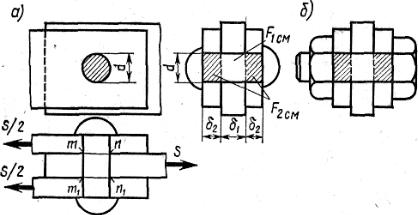
Рассмотрим вначале работу одиночной заклепки, соединяющей три листа (рис. 4.9, а). Одним из видов разрушения указанного соединения является срез заклепки по сечениям т-п и т1-п1, что показано на рис. 4.10. Такая заклепка называется двухсрезной. В аналогичных условиях находится болтовое соединение (рис. 4.9, б). Все дальнейшее, хотя и излагается применительно к заклепкам, относится также и к некоторым видам болтовых соединений (соединения на «черных» болтах).
Рис. 4.9
63
Найдем предельную силу Sср, которую может выдержать одна двухсрезная заклепка по условию среза. При этом за момент выхода из строя соединения будем считать состояние текучести в сечениях среза заклепки, сопровождающееся значительным сдвигом листов.
Можно считать, что в момент текучести в каждой точке сечения среза напряжения достигают расчетного предела текучести, который обозначают через Rср. Следовательно, предполагаем, что в предельном состоянии касательные напряжения распределены равномерно по сечению среза и равны Rср. Поэтому
Sср = FсрRср, |
(4.8) |
где Fcp – площадь двух срезов по сечениям т-п и т1-п1 заклепки, равная площади двух кругов диаметром d (d – диаметр заклепки),
F |
= 2 |
πd 2 |
. |
(a) |
||||
|
|
|||||||
|
ср |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||
Подставляя выражение (а) в формулу (4.8), получим Sср для двух- |
||||||||
срезной заклепки: |
|
|
|
|
|
|
|
|
S |
ср |
= |
πd 2 |
|
R . |
(4.9) |
||
|
|
|||||||
|
2 |
|
ср |
|
||||
|
|
|
|
|
|
|||
Если склепываемый пакет содержит больше трех листов, то заклепка может иметь не два, а большее число срезов. Для заклепки, имеющей k срезов, Sср определяют по формуле
S |
ср |
= k |
πd 2 |
R . |
(4.10) |
|
|||||
|
4 |
ср |
|
||
|
|
|
|
||
Помимо среза при относительно тонких листах возможно нарушение соединения вследствие смятия листов или заклепки в месте их контакта. Фактическое распределение напряжений по поверхности контакта заклепки и листа весьма сложно. Но приближенно опасность смятия может быть оценена не фактической величиной контактных напряжений, а их средним значением, отнесенным к площади проекции поверхности контакта на диаметральную плоскость Fсм = dδ. Последняя называется условной площадью
смятия (рис. 4.11). На рис. 4.9 показана условная площадь смятия под средним листом F1см = δ1d и под крайними листами F2см = 2δ2d. На обе площа-
ди смятия приходится одна и та же сила S, поэтому за расчетную надо при-
нимать минимальную из указанных площадей F min . В общем случае
см
Fсмmin = d ∑δ, |
(4.11) |
где ∑δ – наименьшая суммарная толщина листов, сминаемых в одном направлении.
64
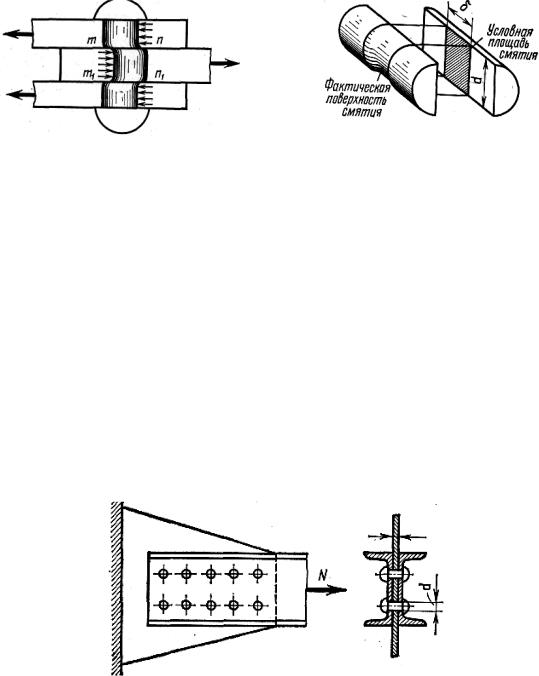
Рис. 4.10 |
Рис. 4.11 |
Экспериментально устанавливается расчетная величина условных напряжений смятия Rсм. Предельная расчетная сила на одну заклепку по смятию равна
S |
см |
= F min R . |
(4.12) |
|
см см |
|
Ясно, что из двух сил, найденных по смятию и по срезу, расчетной для заклепки является меньшая из них.
Обратимся теперь к определению необходимого числа заклепок при действии на соединение силы N (рис. 4.12). Сделаем допущение о том, что сила распределяется между всеми заклепками поровну.
Следует отметить, что в упругой стадии заклепки в соединении работают неравномерно: на концах соединения они более загружены, а в середине – менее. Но в пластической стадии усилия в заклепках выравниваются вследствие текучести, что позволяет пользоваться указанным выше допущением о равномерной загрузке всех заклепок соединения.
t
Рис. 4.12
Необходимое число заклепок найдем по формуле
n = |
N |
, |
(4.13) |
|
|||
|
Smin |
|
|
где Smin – меньшая из двух расчетных предельных сил, которую выдерживает одна заклепка: по срезу (4.10) и по смятию (4.12).
Подбор сечения и проверку прочности соединяемых элементов производят с учетом ослабления их заклепочными отверстиями, т. е. по пло-
щади Fnetto.
65
4.6.2. Расчет сварных соединений на срез
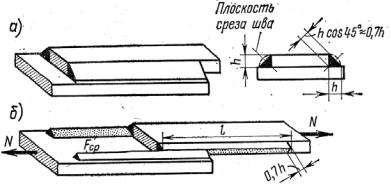
Рассмотрим принцип расчета сварного соединения на примере соединения двух листов угловыми швами (рис. 4.13, а). Сварные соединения не создают ослабления элементов, менее трудоемки, чем другие виды соединения, и потому более экономичны. Они пользуются наибольшим распространением в стальных конструкциях.
Рис. 4.13
Разрушение швов в рассматриваемом соединении происходит от среза по наименьшей возможной площади среза, расположенной в биссекторной плоскости прямого угла, как это показано на рис. 4.13, б. При этом расчетное поперечное сечение шва принимается в виде треугольника.
Обозначая высоту шва через h, получим площадь среза для двух швов Fср = 2lhcos 45o ≈1,4lh.
При составлении условия прочности предполагается равномерное распределение касательных напряжений по площади среза шва. Тогда условие прочности примет вид
N |
= |
N |
≤ Ryсв, |
(4.14) |
|
1,4lh |
|||
Fcp |
|
|
||
где Ryсв – расчетное сопротивление материала углового сварного шва на срез;
l – расчетная длина одного шва, которая берется иногда на 10 мм меньше фактической длины из-за возможного ухудшения качества сварки по концам шва.
Материал шва не имеет, как правило, ярко выраженной площадки текучести. Поэтому в предельном состоянии в сварном шве в отличие от заклепочных соединений касательные напряжения полностью не выравниваются. Исходя из этих соображений, ограничивают длину (l ≤ 60h ). При этом условии отступление от принятого допущения о равномерном распределении касательных напряжений оказывается не слишком велико. С другой стороны, необходимо, чтобы l ≥ 40 мм и l ≥ 4h.
Задавшись высотой шва h, по формуле (4.14) можно найти требуемую длину шва.
66
М-5. КРУЧЕНИЕ
5.0. Введение в модуль
Модуль содержит следующие структурные элементы:
1.Вычисление крутящих моментов и построение их эпюр.
2.Напряжения и деформации при кручении.
3.Потенциальная энергия при кручении.
4.Анализ напряженного состояния при кручении.
5.Кручение стержня с прямоугольным сечением.
Цель модуля – овладение методикой расчета прочности и жесткости при кручении.
5.1. Вычисление крутящих моментов и построение их эпюр
Кручением называют такой случай деформации стержня, при котором в его поперечных сечениях возникают только одни крутящие моменты; нормальная сила, изгибающие моменты и поперечные силы равны нулю. Кручению подвергаются многие детали машин и сооружений: валы двигателей и станков, оси моторных вагонов и локомотивов, элементы пространственных конструкций и т. п. Исследования показали, что характер деформации скручиваемого стержня в значительной степени зависит от формы его поперечного сечения. Среди стержней с различными формами поперечных сечений, подвергаемых кручению, особое место занимают стержни с круглым или кольцевым сечением, имеющие наибольшее распространение в технике.
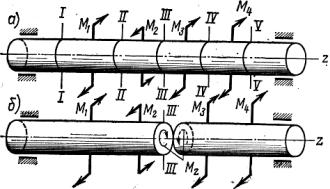
К скручиваемому стержню в разных его сечениях может быть приложено несколько внешних моментов. Рассмотрим случай, когда все внешние моменты взаимно уравновешены и действуют в плоскостях, перпендикулярных оси стержня (рис. 5.1, а):
M1 − M2 + M3 + M4 =0. |
(5.1) |
Для определения крутяще- |
|
гомоментавкаком-либосечении, |
|
например, III-III, мысленно раз- |
|
режем вал по этому сечению на |
|
две части и приложим к каждой |
|
части крутящие моменты М2. Ве- |
|
личину крутящего момента мож- |
|
но найти из условия равновесия |
|
любой из отсеченных частей. Для |
|
этого необходимо приравнять ну- |
|
лю сумму моментов относительно |
|
продольнойосистержня. |
Рис. 5.1 |
67 |
|
Так, например, для случая, показанного на рис. 5.1, б, из уравнения равновесия левой части ∑M z = 0 находим
M1 − M 2 + M z = 0, |
|
откуда |
|
M z = M 2 − M1 . |
(5.2) |
Для случая, когда берется равновесие правой части, имеем |
|
− M z + M3 + M 4 = 0. |
|
Следовательно, |
|
M z = M3 + M 4. |
(5.3) |
Легко заметить, что оба значения крутящего момента Мz равны между собой. Это видно из равенства (5.1).
В общем случае вместо уравнения (5.2) или, соответственно, уравнения (5.3) можно было бы написать:
M z = ∑M Л ,
M z = ∑M П.
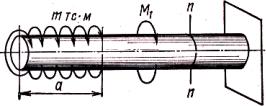
Таким образом, крутящий момент Mz в поперечном сечении стержня равен алгебраической сумме моментов всех внешних сил, действующих на часть стержня по одну сторону от сечения. Так, для случая, показанного на рис. 5.2, момент в сечении п-п опреде-
ляется равенством
a
M n−n = ∫mdz + M1 = ma + M1.
o
Крутящий момент, приложенный к торцовому сечению отсеченной части стержня (см. рис. 5.1), будем считать положительным, если при взгляде на
указанное сечение со стороны его внешней нормали видим момент, направленный по ходу часовой стрелки.
Если найти крутящие моменты в целом ряде сечений, то изменение Мz по длине стержня можно изобразить графически, построив эпюру крутящих моментов. Эпюры Мк строят по участкам; границами участка являются сечения, где приложены сосредоточенные моменты, а также оканчиваются или начинаются распределенные моментные нагрузки. Для произвольного сечения каждого участка составляется аналитическое выражение крутящего момента Мк, по которому строится эпюра крутящих моментов. Положительные моменты на эпюре обычно откладывают вниз, а отрицательные – вверх.
Рассмотрим пример построения эпюры крутящих моментов для стержня, изображенного на рис. 5.3, а.
68
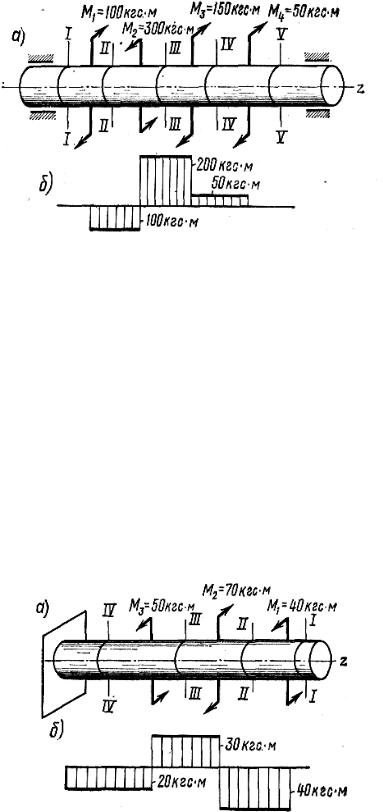
Рис. 5.3
Из равновесия левой отсеченной части, пренебрегая трением в подшипниках, найдем крутящиемоментывсеченияхI-I, II-II, III-III, IV-IV иV-V:
M zI = 0;
M zII = −M1 = −100 кгс м;
M zIII = −M1 + M 2 = −100 +300 = +200 кгс м;
M zIV = −M1 + M 2 − M3 = −100 + 300 −150 = +50 кгс м; M zV = −M1 + M 2 − M3 − M 4 = −100 +300 −150 −50 = 0.
Из этих выражений видно, что в пределах каждого участка крутящий момент является постоянным. Эпюра Мz показана на рис. 5.3, б.
В качестве второго примера рассмотрим построение эпюры крутящих моментов для стержня, показанного на рис. 5.4, а.
Рис. 5.4
При построении эпюры Mк рассмотрим равновесие правой отсеченной части. В этом случае можно не вычислять реактивный момент заделки. Крутящие моменты в сечениях I-I, II-II, III-III, IV-IV равны:
69
M zI = 0;
M zII = −M1 = −40 кгс м;
M zIII = −M1 + M 2 = −40 + 70 = +30 кгс м;
МzIV = −M1 + M 2 − M 3 = −40 + 70 −50 = −20 кгс м.
Эпюра крутящих моментов Mк показана на рис. 5.4, б.
5.2.Напряжения и деформации при кручении стержня
скруглым поперечным сечением
Нанесем на боковую поверхность скручиваемого стержня сетку, образованную системой продольных линий (образующих) и окружностей, составляющих внешние контуры поперечных сечений (рис. 5.5). Оказывается, что после закручивания прямоугольники, образованные сеткой, перекашиваются, ось стержня остается прямолинейной, контуры поперечных сечений (круглые и плоские до деформации) остаются такими же и после деформации. При кручении происходит поворот одного сечения относительно другого на некоторый угол, называемый углом закручивания. Расстояние между поперечными сечениями практически не меняется, а это значит, что
продольные волокна не удлиняются и не укорачиваются. Описанные наблюдения характеризуют деформации
волокон, лежащих на поверхности стержня, но они не позволяют делать какие-либо заключения о деформации внут- Рис. 5.5 ренних волокон. Для того чтобы сделать задачу вполне определенной, сформулируем гипотезы, которые положим в
основу дальнейших выводов. Будем предполагать, что:
1)сечения, плоские до закручивания, остаются плоскими и после закручивания;
2)радиусы, проведенные мысленно в любом поперечном сечении, в процессе кручения не искривляются.
На основании принятых гипотез кручение круглого стержня можно представить как результат сдвигов, вызванных взаимным поворотом поперечных сечений относительно друг друга. Вследствие этого в поперечных сечениях возникают только касательные напряжения, а нормальные напряжения равны нулю.
Рассмотрим стержень радиуса r, заделанный одним концом (рис. 5.6), на свободном конце которого приложим пару сил с моментом М. На боковой поверхности стержня проведем образующую Ке, которая после кручения займет положение Ке'. В результате кручения стержня сечение I-I, взятое на расстоянии z от заделки, повернется на угол ϕ, а со-
70
