
scherbo-sp1
.pdf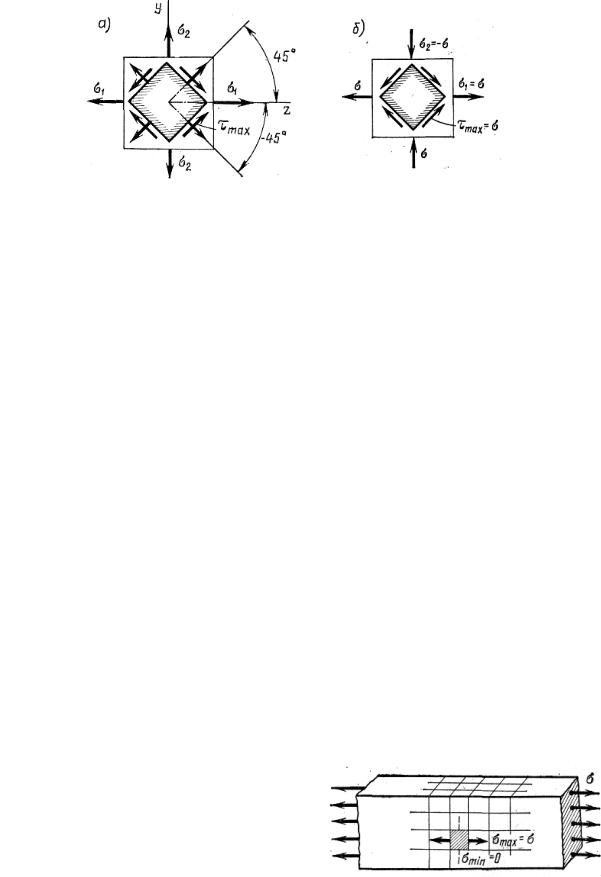
Рис. 3.12
В общем случае на площадках с τmах нормальные напряжения не равны нулю. Действительно, полагая в формуле (3.14) α = ±45° и учитывая
(3.13), получим
|
|
σ + σ |
2 |
|
|
σ |
z |
+ σ |
y |
|
|
σ |
o = |
1 |
= |
|
|
|
(3.18) |
||||
2 |
|
|
|
|
2 |
|
|
||||
|
±45 |
|
|
|
|
|
|
|
|
||
В частном случае, когда на гранях призмы действуют два главных |
|||||||||||
напряжения σ1 = −σ2 = σ |
(рис. 3.12, б), |
экстремальные касательные на- |
|||||||||
пряжения (3.16) численно равны главным напряжениям: |
|
||||||||||
τmax = σ,
а нормальные напряжения на площадках с экстремальными касательными напряжениями в этом случае равны нулю. Такой случай напряженного состояния носит название чистого сдвига, а площадки, на которых действуют одни касательные напряжения, называются площадками чистого сдвига.
3.6. Понятие о траекториях главных напряжений
Наглядное представление о потоке внутренних сил в нагруженном теле дают траектории главных напряжений. Так называется линия, в каждой точке которой касательная совпадает с направлением главного напряжения в этой точке.
При простом растяжении бруса (рис. 3.13) траекториями главных напряжений, очевидно, являются прямые, параллельные и перпендикулярные его оси. Если во всех точках трубы, рассмотренной в конце предыдущего па-
раграфа, наметим направление главных |
|
напряжений, то получим сетку взаимно |
|
ортогональных кривых – траекторий |
|
главных сжимающих и растягивающих |
|
напряжений (рис. 3.14). Прямоуголь- |
|
ный элемент, выделяемый траекто- |
Рис. 3.13 |
риями, испытывает растяжение (сжа- |
|
51 |
|

тие) в перпендикулярных направлениях, а касательные напряжения на его гранях отсутствуют.
Траектории σmin
Рис. 3.14
В указанных примерах величина главного напряжения во всех точках тела одинакова. В общем случае главное напряжение меняет величину при движении вдоль траектории.
3.7. Деформированное состояние в точке
Рассмотрим особенности деформации материала при плоском напряженном состоянии.
Если бесконечно малый прямоугольный элемент с длиной сторон dz и dy ориентирован произвольно, то в общем случае плоского напряженного состояния на него действуют нормальные напряжения σ1, σу и касательные напряжения τzу = τуz (рис. 3.15, а). Возникновение этих напряжений сопровождается деформацией элемента. На количественной связи напряжений и деформаций остановимся позднее, а сейчас обратим внимание лишь на их геометрическую связь. Рассмотрим деформации элемента, развивающиеся в плоскости упомянутых напряжений. Для изотропного материала удлинения сторон элемента связаны с действием нормальных напряжений. Обозначим их через ∆dz и ∆dy (рис. 3.15, б). Линейные деформации в точке, как было указано выше, характеризуются величинами относительных удлинений в соответствующих направлениях:
|
|
εz = |
∆dz |
; |
εy = |
∆dy |
, |
(3.19) |
|||
|
|
dz |
dy |
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
б) |
|
|
|
|
|
|
в) |
|
а) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.15
52
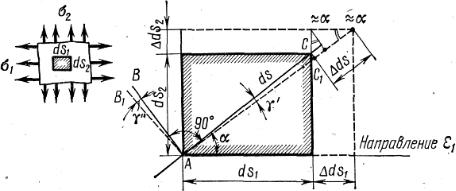
С касательными напряжениями связана угловая деформация, или деформация сдвига. Она заключается в изменении первоначально прямого угла на угол γzу, называемый углом сдвига, показанный на том же рис. 3.15, б.
Представим, что через рассматриваемую точку в направлении осей z и у проходят два взаимно перпендикулярных отрезка длиной dz и dy. В результате деформации указанные отрезки получают относительные удлинения, определяемые по формулам (3.34), а также происходит изменение прямого угла между ними на угол сдвига γzу.
Если мысленно вращать оси z и y вокруг точки их пересечения, последовательно совмещая с различными отрезками, то каждому положению осей
z', у' будут соответствовать свои удлинения εz′, εу′ и угол сдвига γz′y′. Совокупность относительных удлинений и углов сдвига для всевозможных положений осей z' и у' характеризует деформированное состояние в точке.
Как было установлено, любое плоское напряженное состояние сводится к растяжению (сжатию) в двух взаимно перпендикулярных направлениях главными напряжениями σ1 и σ2 (см. пунктир на рис. 3.15, а). Так как на главных площадках касательные напряжения равны нулю, то прямоугольный элемент, ориентированный в направлении σ и σ2, будет испытывать только удлинение, а угол сдвига будет равен нулю (рис. 3.15, б).
Отсюда заключаем, что всегда можно указать два взаимно перпендикулярные направления, проходящие через данную точку, в которых отрезки получают лишь удлинения ε1 и ε2, а прямой угол между ними не изменяется. Указанные относительные удлинения ε1 и ε2 называют главными деформациями в данной точке. В точках упругого и изотропного тела направление главных напряжений и главных деформаций всегда совпадает.
Название «главные деформации» связано с тем, что, подобно главным напряжениям, удлинения ε1 и ε2 имеют экстремальные значения по сравнению с удлинениями в любых направлениях, исходящих из данной точки.
Найдем относительное удлинение εα отрезка, проходящего через рассматриваемуюточку подпроизвольнымугломα кнаправлениюε1 (рис. 3.16).
Рис. 3.16
53
Будем считать главные деформации ε1 и ε2 заданными. Наклонный отрезок длиной ds будем рассматривать как диагональ прямоугольного элемента, выделенного из тела и имеющего длину сторон dsl и ds2 в направлении главных деформаций. Из чертежа находим абсолютное удлинение наклонного отрезка, принимая из-за малости деформаций угол α - γ' ≈ α:
∆ds = ∆ds1 cosα + ∆ds2 sin α.
Искомое относительное удлинение равно
εα = |
∆ds = |
∆ds1 cosα + |
∆ds2 sin α = |
∆ds1 cos2 α + |
∆ds2 sin2 α. |
|||
|
ds |
ds |
|
ds |
|
|
ds1 |
ds2 |
Учитывая, что ∆ds1 = ε |
и ∆ds2 = ε |
2 |
, окончательно получим |
|||||
|
ds1 |
1 |
ds2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
ε |
α |
= ε cos |
2 α + ε |
2 |
sin2 α. |
(3.20) |
||||
|
1 |
|
|
|
|
|
|
|||
Используя тригонометрическую зависимость (3.5), формулу (3.20) |
||||||||||
можно представить в следующем виде: |
|
|
|
|
||||||
εα = |
ε1 + ε2 |
|
+ |
ε1 − ε2 |
cos 2α. |
(3.21) |
||||
|
|
|
||||||||
|
|
2 |
2 |
|
|
|
||||
Пусть ε1 > ε2. Тогда из формулы (3.21) следует, что εα достигает наибольшего значения при cos2α = 1 , т. е. при α = 0. При этом
εαmax = ε1.
Наоборот, при 2α = 180° cos2α = – 1 и εα достигает минимального значения:
εαmin = ε2.
Если величина и направление главных деформаций в точке известны, то относительное удлинение по любому направлению определяется по формуле (3.20) или (3.21).
3.8.Аналогия между зависимостями для напряженного
идеформированного состояний в точке
Найдем угол сдвига между двумя взаимно перпендикулярными отрезками АС и АВ, расположенными под углом α к направлениям главных деформаций (рис. 3.16).
Отрезок АС в результате деформации повернулся на угол γ', который по малости можно определить как отношение дуги СС1 к радиусу АС = ds:
γ′ = |
CC1 |
= |
∆ds1 sin α |
− |
∆ds2 cos α |
, |
ds |
ds |
ds |
||||
|
|
|
54 |
|
|
|

или |
∆ds |
|
|
∆ds |
|
ε |
−ε |
|
|
|
|
|
|
|
|
|
|||||
γ′ = |
ds 1 sin αcos α − |
|
ds 2 cos αsin α = |
1 |
2 |
2 sin 2α. |
(3.22) |
|||
|
1 |
|
|
2 |
|
|
|
|
|
|
Для определения γ" – угла поворота линии АВ – в формуле (3.22) |
||||||||||
угол α надо заменить на (α + 90°). Тогда получим |
|
|
||||||||
|
γ |
′′ |
= − |
|
ε1 − ε2 |
sin 2α. |
|
|
|
(3.23) |
|
2 |
|
|
|
||||||
|
|
|
|
|
||||||
Разные знаки в формулах (3.22) и (3.23) говорят о том, что отрезки АС и АВ поворачиваются от недеформированного положения в разные стороны, как это и показано на рис. 3.16. Примем γα > 0, если прямой угол АВС
уменьшается. Так как выражения (3.22) и (3.23) отвечают увеличению этого угла на (ε1 −ε2 )sin 2α, то выражение для γα следует записать в виде
γα = −(ε1 − ε2 )sin 2α. |
(3.24) |
Формулы (3.21) и (3.24), описывающие плоское деформируемое состояние,
εα = ε1 + ε2 |
+ |
ε1 −ε2 |
cos 2α, |
|||
|
γα |
2 |
|
2 |
(3.25) |
|
|
= − ε1 −ε2 sin 2α |
|||||
2 |
||||||
|
|
2 |
|
|||
и выражения (3.14) и (3.15), описывающие плоское напряженное состояние в точке,
σα = |
σ1 + σ2 |
+ σ1 − σ2 |
cos 2α, |
|
2 |
2 |
(3.26) |
|
τα = − σ1 −σ2 sin 2α |
||
|
|
2 |
|
структурно идентичны.
Следовательно, они указывают на математическую аналогию зако-
нов распределения напряжений σα, τα и деформаций εα и 12 γα в точке. Эта
аналогия не случайна и связана с тем, что деформированное состояние в точке вполне определяется матрицей деформаций ТД, компонентами которой для деформаций в плоскости zу являются
|
εz |
1 |
|
|
|
|
2 |
γzy |
|||
TД = |
1 |
γzy |
|
. |
|
|
2 |
εy |
|
||
|
|
|
|
|
|
|
|
55 |
|
|
|

При повороте осей компоненты TД преобразуются аналогично компонентам матрицы напряжений ТН (3.8).
На основании указанной аналогии можно без вывода написать, например, формулу
|
|
εz + εy |
|
1 |
|
|
|
|
2 |
|
1 |
|
|
2 |
|
ε |
= |
|
± |
|
(ε |
|
−ε |
|
) |
+ 4 |
|
γ |
|
. |
(3.27) |
2 |
2 |
|
|
2 |
|||||||||||
1,2 |
|
|
|
z |
|
y |
|
|
|
zy |
|
|
Она записана по аналогии с формулой (3.13), где напряжения σZ, σу и τzy
заменены соответствующими деформациями εz, εу и 12 γzy .
Формула (3.27) дает возможность определить главные деформации ε1 и ε2 в точке через удлинения в двух произвольных взаимно перпендикулярных направлениях εz, εу и соответствующий угол сдвига γzу.
Из (3.27) следует, что
ε1 + ε2 = εz + εy = const,
т. е. сумма относительных удлинений по любым взаимно перпендикулярным направлениям в данной точке есть величина постоянная. Аналогич-
ное положение выражается формулой (3.9) в напряженном состоянии.
В заключение можно сказать, что здесь были рассмотрены лишь деформации, развивающиеся в плоскости двух главных напряжений. В общем случае деформации материала в точке носят объемный характер. При этом полученная выше в плоской задаче математическая аналогия в распределении деформаций и напряжений сохраняется и в объемной задаче.
Поэтому в общем случае в каждой точке тела можно указать три главные деформации: ε1, ε2 и ε3 – относительные удлинения малых отрезков, ориентированных в трех взаимно перпендикулярных направлениях, между которыми отсутствует угол сдвига.
Аналогично тензору напряжений вводится понятие тензора деформаций. Его матрица вполне характеризует деформированное состояние в точке. Тензор деформацийдляосей, совпадающихснаправлениямиε1, ε2, ε3, имеетвид
|
ε |
0 |
0 |
|
|
ТД = |
|
1 |
ε2 |
0 |
|
|
0 |
. |
|||
|
|
0 |
0 |
ε3 |
|
|
|
|
|||
В точках упругого изотропного тела направления главных деформаций всегда совпадают с направлениями трех главных напряжений σl, σ2 и σ3.
56
М-4. СДВИГ
4.0. Введение в модуль
Модуль содержит следующие структурные элементы:
1.Понятие о чистом сдвиге.
2.Анализ напряженного состояния при чистом сдвиге.
3.Закон Гука при чистом сдвиге.
4.Зависимости между модулями сдвига и Юнга.
5.Потенциальная энергия при чистом сдвиге.
6.Практические расчеты прочности при сдвиге.
Цель модуля – анализ распределения напряжений при сдвиге, овладение методикой расчета прочности при сдвиге.
4.1.Понятие о чистом сдвиге
Внекоторых случаях прочность, а также жесткость элементов конструкции непосредственно связаны с сопротивлением материала сдвигу. Отсюда появляется необходимость изучения деформации сдвига и соответствующего ей напряженного состояния.
Из понятия о деформированном состоянии в точке следует, что в его состав всегда в общем случае входит и деформация сдвига. Для более тщательного изучения этой деформации было введено понятие чистого сдвига.
При чистом сдвиге прямоугольный элемент, выделенный в окрестности некоторой точки и ориентированный определенным образом, испытывает только деформацию сдвига, а удлинения его сторон отсутствуют. По граням указанного элемента действуют только касательные напряже-
ния (рис. 4.1). Таким образом, чистым сдвигом называют такой вид плоского напряженного и деформированного состояния, при котором на двух взаимно перпендикулярных площадках, ориентированных определенным образом, действуют только касательные напряжения.
Указанные площадки называют площадками чистого сдвига. Принимая эти площадки за исходные и полагая в формулах (3.3) и (3.4) преды-
дущей главы σz = σy = 0, τzy = τ, получим:
σα = τsin 2α, |
(4.1) |
τα = τcos 2α. |
(4.2) |
Формула (4.1) указывает, что σα обращается в нуль только на площад-
ках чистого сдвига (при α = 0 или n π2 ). На всех других площадках нормаль-
ные напряжения не равны нулю, как это показано на рис. 4.2 для элемента, повернутого на произвольный угол α к площадкам чистого сдвига.
57
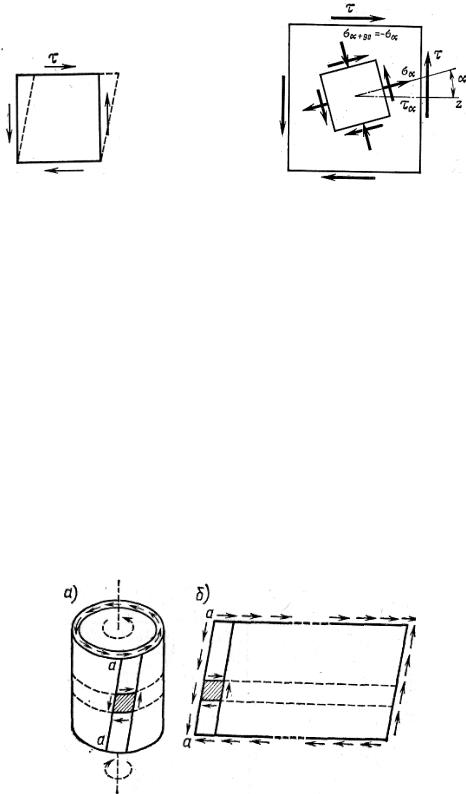
Рис. 4.1 |
Рис. 4.2 |
Интересно отметить следующую особенность нормальных напряжений при чистом сдвиге: на любых взаимно перпендикулярных площадках они равны по величине и противоположны по знаку, т. е. σα+90o = −σα,
что следует из (4.1) и равенства sin2(α+ 90°) = -sin2α, а также из (3.9), где надо положить σz = 0 и σу = 0. Таким образом, при чистом сдвиге наблюдается своеобразный «закон парности нормальных напряжений», по форме аналогичный закону парности касательных напряжений. Отсюда как част-
ный вывод следует, что при чистом сдвиге главные напряжения удовлетворяют условию σ1 = −σ2.
Типичным примером тела, во всех точках которого имеет место чистый сдвиг, является скручиваемая тонкостенная труба, показанная на рис. 4.3, а. Вследствие относительного поворота концевых сечений образующие трубы наклоняются и ее стенки испытывают деформацию сдвига. Если разрезать мысленно трубу вдоль образующей а-а и развернуть ее, то можно видеть, что трубапредставляетсобойпластину, испытывающуючистыйсдвиг(рис. 4.3, б).
Рис. 4.3
Заметим, что деформация кручения часто используется для экспериментального изучения работы материалов на сдвиг, так как практически не удается создать напряженное состояние чистого сдвига путем непосредственного приложениякасательныхнапряженийккромкамплоскойпластинки.
58

4.2. Анализ напряженного состояния при чистом сдвиге
Найдем величину экстремальных напряжений при чистом сдвиге с
помощью формул (4.1) и (4.2). Первая из них указывает, что при α = 45o (sin 2α =1) имеет место максимальное нормальное напряжение σ1 = τ, а
при α =135o (sin 2α = −1) – минимальное напряжение σ2 = −τ. Экстре-
мальные касательные напряжения можно определить по формуле (4.2):
при α = 0 τmax = τ.
Итак, при чистом сдвиге главные напряжения – сжимающее и растягивающее – равны между собой и численно равны экстремальным касательным напряжениям. Главные площадки составляют с площадками
чистого сдвига угол 45° (рис. 4.4). |
|||||
Естественно, что те же самые результаты по- |
|||||
лучаются и по общим формулам (3.13), где надо по- |
|||||
ложить |
σz = σy = 0, |
τzy = τ, после чего они дадут |
|||
σ = ± |
τ2 , откуда σ |
|
= τ и σ |
2 |
= −τ. |
1,2 |
1 |
|
|
||
Чистый сдвиг представляет собой единствен- |
|
|
ный вид плоского напряженного состояния, при ко- |
|
|
тором отсутствует изменение объема материала, а |
|
|
любой выделенный элемент изменяет только форму |
Рис. 4.4 |
|
(при малых деформациях). |
||
|
4.3. Закон Гука при чистом сдвиге
Рассмотрим деформацию элемента, ограниченного площадками чистого сдвига (рис. 4.5).
Величину δ называют абсолютным сдвигом, а отношение δ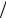 α ≈ γ –
α ≈ γ –
относительным сдвигом, или углом сдвига. С понятием угла сдвига мы уже встречались в М-3. Экспериментально установлено, что в определенных пределах деформация сдвига происходит упруго, а величина ее пропорциональна касательным напряжениям τ:
γ = τ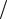 G
G
или
τ =Gγ. |
(4.3) |
Это соотношение называют законом Гука при сдвиге.
Коэффициент пропорциональности G между касательным напряже-
нием и углом сдвига называют модулем упругости при сдвиге, или моду-
лем упругости второго рода, в отличие от модуля Е при растяжении – сжатии, называемого модулем упругости первого рода.
59
Из выражения (4.3) следует, что модуль G имеет размерность напряжений (кгс/см2), так как γ – величина безразмерная. Для каждого материала модуль сдвига G имеет свое значение. Так, для стали G ≈ 8 105 кгс/см2, для алюминия G ≈ 2,7 105 кгс/см2. Величина модуля G определяется экспериментально, например, из опытов на кручение трубчатых образцов.
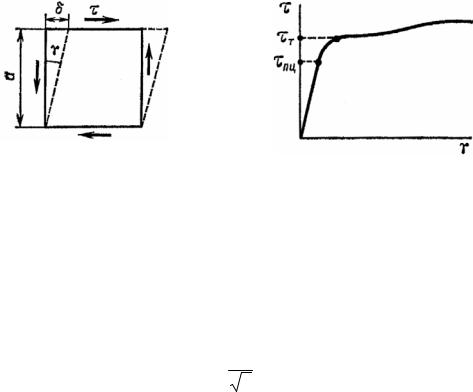
Типичный вид диаграммы τ – γ деформации сдвига для пластичной стали показан на рис. 4.6. Эта диаграмма, получаемая также из опытов на кручение, напоминает аналогичную диаграмму при растяжении.
Рис. 4.5 |
Рис. 4.6 |
Напряжение τпц – предел пропорциональности при сдвиге – является границей справедливости закона Гука (4.3). Точка τ = τт определяет предел текучести при сдвиге. Так же как и при растяжении, при постоянном напряжении τ = τт наблюдается значительный рост сдвигов (текучесть при сдвиге), сменяющийся затем стадией упрочнения (некоторым повышением напряжений с ростом сдвигов). Характерно, что для многих материалов величина τт связана с пределом текучести при растяжении σт соотношением
τт ≈ |
σт . |
(4.4) |
|
3 |
|
4.4. Зависимость между модулями упругости при растяжении и при сдвиге
Удлинение ∆s диагонали АС на рис. 4.7, а можно объяснить двояко. С одной стороны, оно является непосредственным следствием деформации сдвига и, значит, при заданных напряжениях τ зависит от модуля G. С другой стороны, диагональ АС можно представить как волокно материала, растягиваемое напряжением σ1 и сжимаемое в поперечном направлении напряжением σ2. В этом случае его удлинение определяется модулем Е. Сказанное позволяет сделать вывод о том, что модули G и Е не являются независимыми друг от друга. К этой же мысли можно прийти из рассмотрения рис. 4.7, б, где деформация сдвига элемента ABC, идентичная де-
60
