
scherbo-sp1
.pdf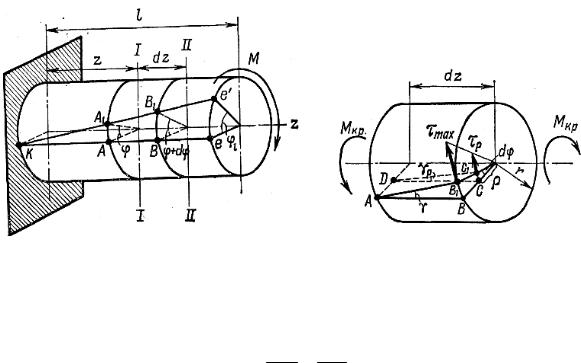
седнее с ним сечение II-II – на угол ϕ+ dϕ. Следовательно, сечение II-II по
отношению к сечению I-I повернется на угол dϕ.
Рассмотрим отдельно элемент стержня длиной dz. Для удобства левое его сечение будем считать неподвижным (рис. 5.7).
Рис. 5.6 |
Рис. 5.7 |
Образующая АВ отклонится на малый угол γ и перейдет в положение АВ1. Угол сдвига волокна, лежащего на поверхности стержня, определяется равенством
γ = BBAB1 = rddzϕ.
Для произвольного волокна, отстоящего от центра стержня на расстоянии ρ, будем иметь
γ0 = |
CC1 |
= |
|
ρdϕ |
. |
|
||||
DC |
|
|
|
|
|
|||||
|
|
|
|
dz |
|
|||||
На основании закона Гука при сдвиге для двух указанных точек |
||||||||||
можно записать: |
|
dϕ |
|
|
|
|
||||
τ = γG = G |
r; |
(5.4) |
||||||||
|
|
|||||||||
|
|
|
dz |
|
||||||
τρ = γ0G = G |
dϕ |
ρ. |
(5.5) |
|||||||
|
||||||||||
|
|
|
|
|
dz |
|
||||
Сопоставляя формулы (5.4) и (5.5), замечаем, что касательные напряжения в точках поперечного сечения изменяются пропорционально расстоянию этих точек от оси стержня. Наибольшие напряжения наблюдаются в точках, наиболее удаленных от центров стержня.
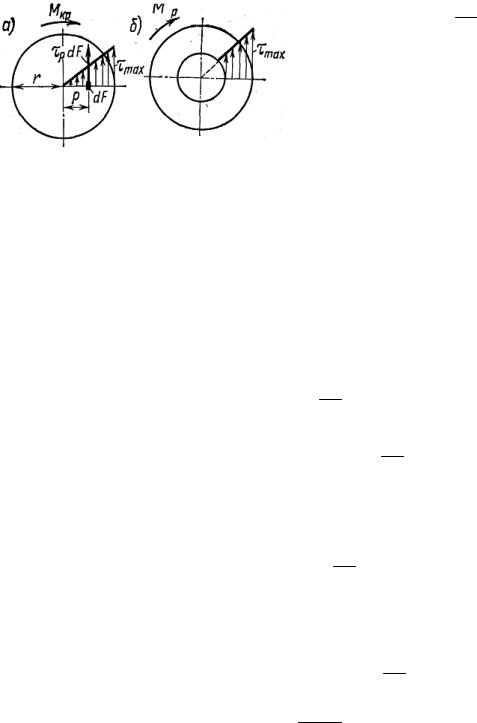
Таким образом, нами был рассмотрен закон изменения τ по радиусу поперечного сечения круглого стержня. Графически этот закон представлен на рис. 5.8, а. Для стержня кольцевого сечения закон распределения касательных напряжений показан на рис. 5.8, б.
71
Величина dϕ , входящая в
|
dz |
|
|
формулы (5.4) и (5.5), может быть |
|
|
найдена из условия, что касательные |
|
|
напряжения, действующие по попе- |
|
|
речному сечению стержня, приво- |
|
|
дятся к паре, момент которой равен |
|
Рис. 5.8 |
крутящему моменту Мк. Выделим |
|
вокруг произвольной точки площад- |
||
|
ку dF, на которой будет действовать элементарная касательная сила τρdF (см. рис. 5.8, а). Момент этой силы относительно оси стержня равен
dM кр = τρdFρ.
Суммируя элементарные моменты, найдем полный крутящий момент
Mкр = ∫τρdFρ. |
(5.6) |
F |
|
Подставляя в формулу (5.6) вместо τρ его значение из (5.5), получим
M кр = F∫GρddzϕdFρ.
Вынесем за знак интеграла величину G ddzϕ , так как для всех точек
поперечного сечения она одинакова, а также заметим, что выражение
∫ρ2dF = Jρ представляет собой полярный момент инерции сечения. Тогда
F
M кр = GJρ ddzϕ,
или |
M кр |
= |
dϕ |
. |
|
GJρ |
dz |
||||
|
|
|
Подставляя в формулу (5.5) найденное значение ddzϕ , окончательно получим
τρ = MJкрρ.
ρ
Эта формула позволяет определять τ в любой точке круглого поперечного сечения. Максимальные напряжения в крайних точках сечения определяют по формуле
τmax = |
M кр |
r = |
M кр |
. |
(5.7) |
|
Jρ |
Wρ |
|||||
|
|
|
|
72
Величину Wρ = Jrρ называют полярным моментом сопротивления кругло-
го сечения.
Как уже указывалось, полярный момент инерции для сплошного круглого сечения
Jρ = |
πr 4 |
= |
πd 4 |
; |
|
2 |
32 |
||||
|
|
|
для кольцевого сечения с внешним диаметром D и внутренним d
Jρ = |
π |
(D |
4 |
− d |
4 |
) = |
πD4 |
(1 − α |
4 |
), |
32 |
|
|
32 |
|
||||||
где α = d D. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Следовательно, моменты сопротивления имеют следующие значения: для сплошного сечения
|
W = |
Jρ |
= πd 3 |
; |
|||
|
|
||||||
|
|
ρ |
d 2 |
16 |
|
||
для кольцевого сечения |
|
|
|
|
|||
|
Jρ |
= πD3 (1 −α4 ). |
|||||
W |
= |
||||||
|
|||||||
ρ |
D 2 |
16 |
|
||||
|
|
|
|||||
При определении угла закручивания воспользуемся уравнением (а), из которого находим
dϕ = M крdz . GJρ
После интегрирования получим полный угол закручивания стержня
l |
M кр |
dz . |
(5.8) |
|
ϕl = |
|
|||
GJρ |
||||
0∫ |
|
|
Если по всей длине стержня момент не меняется и стержень имеет постоянный диаметр, интегрируя выражение (5.8), получим
ϕl = |
M крl |
. |
(5.9) |
|
GJρ |
||||
|
|
|
Величину GJρ называют жесткостью стержня при кручении. Она
характеризует сопротивление стержня закручиванию.
Для ступенчатых стержней или же для стержней, у которых Мк меняется по длине скачкообразно, угол закручивания между начальным и конечным сечениями стержня подсчитывается как сумма углов закручивания по участкам с постоянным Мкр/Jρ:
n |
|
M кр |
li |
|
ϕ = ∑ |
|
i |
|
(5.10) |
|
GJρi |
|||
i=1 |
|
|
||
|
73 |
|
|
|
Полный угол закручивания не всегда может характеризовать жесткость стержня при кручении. На протяжении длины стержня крутящие моменты могут иметь разные знаки, поэтому полный угол закручивания, найденный по формуле (5.10), может быть небольшим, в то время как на отдельных участках он окажется значительным. Для оценки жесткости стержня вводится другая мера – относительный угол закручивания
θ = |
M кр |
, |
(5.11) |
|
GJρ |
||||
|
|
|
имеющая размерность 1/см или 1/м.
Для случаев, когда на отдельных участках стержня эпюра Мк постоянна, величина θ численно равна углу закручивания вала на единицу длины.
5.3. Потенциальная энергия при кручении круглого вала
Будем считать, что материал стержня при кручении работает при напряжениях, не превышающих предел упругости. В этом случае работа внешних сил А, затрачиваемая на кручение стержня, Мкр равна количеству потенциальной энергии U, накоп-
ленной в стержне, т. е
A =U.
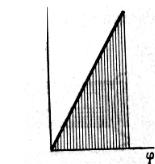
РаботаАравнаплощадидиаграммы кручения(рис. 5.9):
|
|
|
|
|
A =U = |
1 M крϕ, |
||
|
|
|
|
|
|
|
|
2 |
|
ϕ |
где Мкр – крутящий момент; |
|
|
||||
|
|
|
|
|||||
Рис. 5.9 |
ϕ – угол закручивания стержня. |
|||||||
|
|
Подставим в формулу (5.12) вместо ϕ |
||||||
их значения из формулы (5.9), тогда |
|
|
|
|
|
|
||
|
|
U = |
M кр2 l |
= |
|
ϕ2GJρ |
. |
|
|
|
2GJρ |
|
2l |
|
|||
|
|
|
|
|
|
|
||
(5.12)
или Mкр
(5.13)
Формулами (5.12) и (5.13) можно пользоваться при ступенчатом изменении крутящих моментов и жесткости стержня. В этом случае потенциальная энергия равна сумме потенциальных энергий, найденных по участкам с постоянным Mкp/Jp.
5.4.Анализ напряженного состояния при кручении. Главные напряжения и главные площадки
Выше было установлено, что в поперечном сечении круглого стержня при кручении возникают касательные напряжения. На основании закона парности касательных напряжений они возникают также и в продольных сечениях (рис. 5.10). Нормальные напряжения как в поперечных, так и в
74
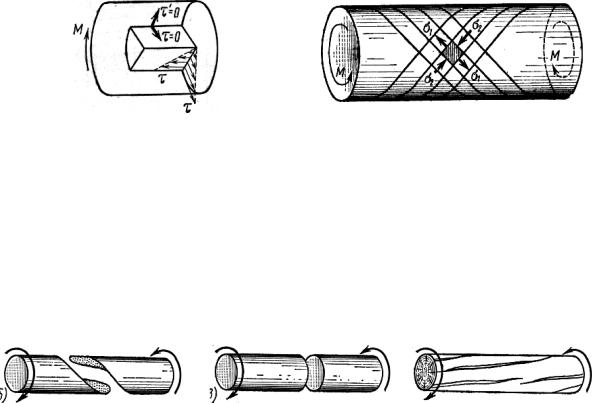
продольных сечениях равны нулю. Вдоль радиуса касательные напряжения также отсутствуют. Если бы эти касательные напряжения имели место, то по закону парности такие же по величине касательные напряжения возникали бы по боковой поверхности, чего на самом деле нет. Таким образом, на двух взаимно перпендикулярных площадках, одна из которых лежит в плоскости поперечного сечения, а другая – в плоскости продольного диаметрального сечения, действуют только касательные напряжения. Такое напряженное состояние называется чистым сдвигом. Из свойств указанного напряженного состояния следует, что по площадкам, наклоненным под углом 45° к оси стержня, действуют главные растягивающие или сжимающие нормальные напряжения. Траектория этих напряжений представляет винтовую линию, наклоненную под углом 45° к образующей. Если поверхность стержня разделить этими винтовыми линиями на прямоугольные клетки, то в одном направлении эти клетки испытывают растяжение, а в другом – сжатие (рис. 5.11). По величине главные напряжения σ1 и σ2 во всех точках сечения равны касательным напряжениям τ.
Рис. 5.10 |
Рис. 5.11 |
Этим объясняется, что стержни, изготовленные из хрупкого материала, хуже работающего на растяжение, чем на сжатие, например, из чугуна, разрушаются по винтовой поверхности от действия главных растягивающих напряжений (рис. 5.12, а). Стержень, изготовленный из пластичной стали, разрушается по поперечному сечению в виде среза (рис. 5.12, б), так как растягивающие напряжения для такого стержня менее опасны, чем касательные. При разрушении деревянного стержня (рис. 5.12, в) происходит скалывание вдоль волокон, так как прочность древесины в этом направлении меньше, чем поперек волокон.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
в) |
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.12
5.5. Кручение стержня с прямоугольным сечением
Задача кручения стержней с некруглым поперечным сечением является значительно более сложной по сравнению с рассмотренной задачей кручения круглых стержней. Так, например, нарушается закон плоских се-
75
чений. Отдельные точки сечения перемещаются вдоль оси стержня, и все сечение в целом перестает быть плоским. Происходит так называемая де-
планация сечения.
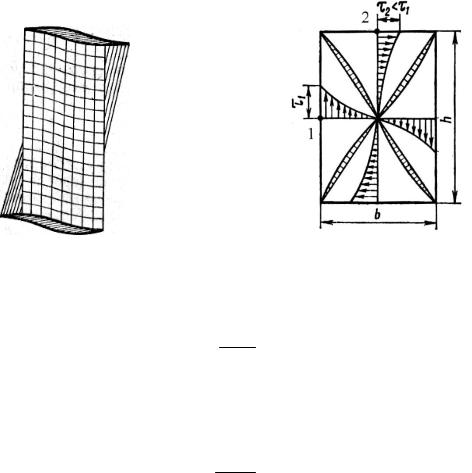
Для прямоугольного сечения это показано на рис. 5.13. Точное решение для некоторых типов поперечного сечения дается в теории упругости. Ограничимся приведением окончательного результата для стержня прямоугольного сечения. На рис. 5.14 показано прямоугольное сечение, на котором изображены эпюры касательных напряжений по главным осям сечения и по диагонали. В угловой точке напряжения равны нулю.
Рис. 5.13 |
Рис. 5.14 |
Наибольшее напряжение развивается в середине длинной стороны (в точке 1). Его можно определить по формуле
τ1 = M кр ,
Wк
где Wк = βb3.
Через τ2 выражается напряжение в середине короткой стороны τ2 = γτ1, а угол закручивания определяется по формуле
ϕ = M крl ,
GJα
где Jα = αb4.
Входящие в эти формулы коэффициенты α, β, γ зависят от соотношения сторон прямоугольника m = h/b. Для некоторых значений m величины α, β, γ даются в табл. 5.1.
|
|
|
|
|
|
|
|
Таблица 5.1 |
|
|
|
|
|
|
|
|
|
|
|
m |
α |
β |
γ |
|
m |
α |
β |
|
γ |
1 |
0,140 |
0,208, |
1,0 |
|
4,0 |
1,123 |
1,150 |
|
0,745 |
1,5 |
0,294 |
0,346 |
0,859 |
|
6,0 |
1,789 |
1,789 |
|
0,743 |
2,0 |
0,457 |
0,493 |
0,795 |
|
8,0 |
2,456 |
2,456 |
|
0,742 |
3,0 |
0,790 |
0,801 |
0,753 |
|
10,0 |
3,123 |
3,123 |
|
0,742 |
|
|
|
|
76 |
|
|
|
|
|
М-6. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
6.0. Введение в модуль
Модуль содержит следующие структурные элементы:
1.Основные понятия.
2.Моменты инерции простейших фигур.
3.Зависимость между моментами инерции относительно параллельных осей.
4.Зависимость между моментами инерции при повороте осей. Главные оси инерции и главные моменты инерции.
5.Эллипс инерции и его свойства.
6.Вычисление моментов инерции сложных фигур.
Цель модуля – определение геометрических характеристик сечений стержней для использования их при определении напряжений.
6.1. Основные понятия
При изучении растяжения и сжатия прямых стержней было установлено, что сопротивление стержня пропорционально площади поперечного сечения. Чем больше площадь поперечного сечения, тем меньше напряжение и удлинение стержня.
Картина резко меняется, если сила приложена к стержню перпендикулярно его оси. Так, если на заделан- а)
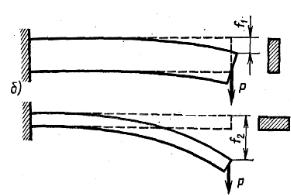
ный одним концом стержень с поперечным сечением в виде вытянутого прямоугольника действует сила, приложенная на другом конце, то стержень будет изгибаться и сечение под грузом переместится на некоторую величину f1 (рис. 6.1, а).
Если стержень повернуть на угол 90° вокруг его оси так, чтобы наибольший размер поперечного сечения рас-
положился горизонтально, то под действием той же вертикальной силы конец стержня опустится на величину f2 (рис. 6.1, б), значительно большую, чем f1. Таким образом, при одной и той же площади в зависимости от ориентировки поперечного сечения стержень по-разному сопротивляется действию силы. Отсюда можно сделать заключение, что площадь поперечного сечения не может характеризовать сопротивляемость стержня изгибу.
Оказывается, что при изучении изгиба, кручения и других случаев деформации стержня необходимо привлекать более сложные геометриче-
77
ские характеристики сечения. В связи с этим возникает задача об изучении некоторых геометрических свойств различных плоских фигур.
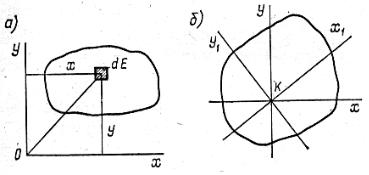
Рассмотрим плоскую фигуру, показанную на рис. 6.2, а. Проведем через произвольную точку систему координат Оху. Выделяя элемент площади dF, составим выражения:
Sx = ∫ ydF; |
S y = ∫xdF. |
F |
F |
Эти геометрические характеристики называются статическими моментами относительно осей Ох и Оу. Они измеряются в см3.
Из теоретической механики известно, что координаты центра тяжести площади фигуры определяют по формулам:
|
|
|
∫xdF |
|
|
x0 |
= |
|
F |
, |
|
|
F |
||||
|
|
|
|
|
|
|
|
|
∫ ydF |
|
|
y0 |
= |
F |
|
. |
|
F |
|
||||
|
|
|
|
|
|
Поэтому
Sx = y0 F, S y = x0 F.
Из последних выражений видно, что статические моменты фигуры относительно осей, проходящих через центр тяжести этой фигуры, равны нулю. Оси координат, проходящие через центр тяжести фигуры, называ-
ются центральными осями.
Рис. 6.2
В дальнейшем мы встретим геометрические характеристики, привычислениикоторыхэлементплощадиdF умножаетсянаквадратрасстояниядооси:
J x = ∫ y2dF,
F
J y = ∫x2dF.
F
78
Эти величины называются осевыми моментами инерции. Составляя интеграл, в котором площадка dF умножается на произведение координат,
получим центробежный момент инерции
J xy = ∫ xydF.
F
Отметим еще одну характеристику, в которой подынтегральное выражение представляет собой произведение элемента площади на квадрат расстояния до начала координат:
Jρ = ∫ρ2dF.
F
Эту величину называют полярным моментом инерции.
Приведенные моменты инерции измеряются в единицах длины, взятой в четвертой степени, например, см4 или м4.
Осевые и полярный моменты инерции всегда положительны, так как под интегралом координаты у, х и ρ берутся в квадратах. Полярный момент инерции
Jρ = ∫ρ2dF = ∫( y2 + x2 )dF = Jx + J y
F
равен сумме двух осевых моментов инерции.
Если через какую-либо точку К фигуры (рис. 6.2, б) провести две системы прямоугольных осей (Ку, Кх и Ку1, Kxl) и определить моменты инерции относительно этих осей, то получим равенство
J x + J y = J x |
+ J y |
(6.1) |
1 |
1 |
|
Это равенство следует из того, что каждая из |
|
|
указанных сумм порознь равна полярному мо- |
|
|
менту относительно точки К. |
|
|
Центробежный момент инерции берется от- |
|
|
носительно двух осей. Он может быть положитель- |
|
|
ным, отрицательным и. равным нулю. Случай, ко- |
|
|
гда центробежный момент инерции равен нулю, |
|
|
заслуживает особого изучения, поэтому он подроб- |
Рис. 6.3 |
|
нобудетрассмотрен ниже. |
|
|
Известно, что интеграл по площади равен сумме интегралов, взятых по отдельным частям, составляющим эту площадь. Поэтому при вычислении моментов инерции сложной фигуры относительно какой-либо оси можно последнюю разбить на ряд простейших фигур (рис. 6.3) и для каждой из них вычислить момент инерции относительно этой оси.
Тогда момент инерции всей фигуры определяется как сумма моментов инерции составных частей:
J x = J1x + J2x + J3x .
79
Подчеркнем, что моменты инерции всех составных частей должны вычисляться относительно одной и той же оси. Суммировать моменты инерции частей фигуры относительно различных осей нельзя.
6.2. Моменты инерции простейших фигур
Вычисление моментов инерции некоторых простейших фигур может быть проведено непосредственным интегрированием по общим выражениям, приведенным в п. 6.1. Рассмотрим несколько наиболее распространенных фигур.
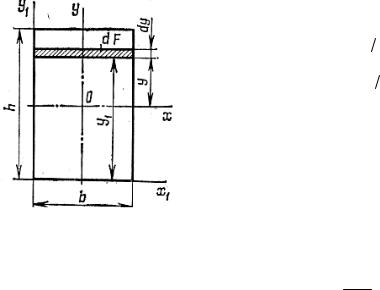
Прямоугольник. Найдем сначала момент инерции относительно центральной оси Ох (рис. 6.4):
J x = ∫ y2dF.
F
Мысленно разобьем прямоугольник на элементарные площадки линиями, параллельными оси Ох. Площадь одного произвольного элемента, как видно из рис. 6.4, определяется равенством
Рис. 6.4
а также
dF = bdy.
Вычисления дают:
h 2 |
y2dy = bh |
3 |
|
J x = b ∫ |
|
. |
|
−h 2 |
12 |
|
|
Таким же образом можно вычислить момент инерции относительно другой оси, проходящей через центр тяжести:
J y = |
hb3 |
. |
|
12 |
|||
|
|
Для оси, проходящей через основание, имеем
J x1 = bh∫ y12dy1 = bh33 ,
0
J y = |
hb3 |
. |
|
3 |
|||
1 |
|
Найдем теперь центробежный момент инерции относительно этих осей. Выбирая, так же как и в предыдущем случае, в качестве элементарной
80
