scherbo-sp1

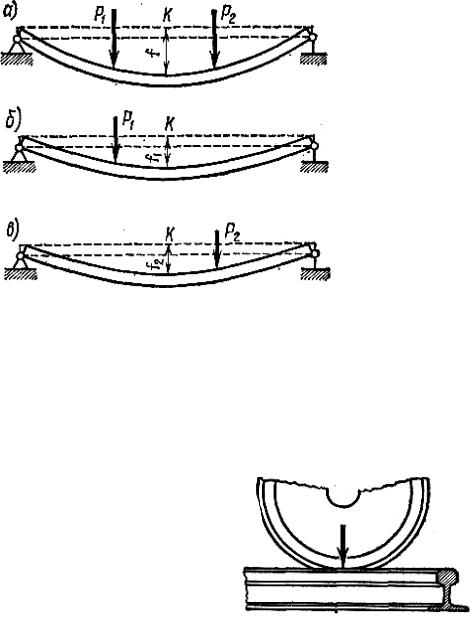
Рис. 1.2

1.2.Виды нагрузок и схематизация элементов сооружений

Всопротивлении материалов различают несколько видов нагрузок, действующих на сооружения.

Сосредоточенные силы. Эти силы передаются на сооружение через небольшую площадку, и практически условно считают, что они приложены в точке. К числу таких сил относится, например, давление обода колеса на рельс (рис. 1.3), если последний рассматривается как длинная балка. В то же время при исследовании местных деформаций в материале (под грузом) необходимо учитывать фактическую передачу усилия че-

понятие сосредоточенной силы является условным. Одна и та же нагрузка в зависимостиотпоставленнойзадачи можетбытьсхематизированапо-разному.

Распределенная нагрузка передается на сооружение через определенную площадь и измеряется в единицах силы, отнесенной к единице площади, – тc/м2, кгс/см2, кгс/мм2 и т. п. По СИ распределенная нагрузка измеряется в ньютонах, отнесенных к единице площади; н/м2. К числу таких нагрузок относятся давление снега на кровлю, давление зерна на дно и стенки силосной башни (рис. 1.4, а), давление воды на плотину (рис. 1.4, б) и т. п. При расчете многих элементов конструкции распределенную по площади нагрузку, как показано на рис. 1.5, а, заменяют нагрузкой, которая относится к единице длины балки.

11

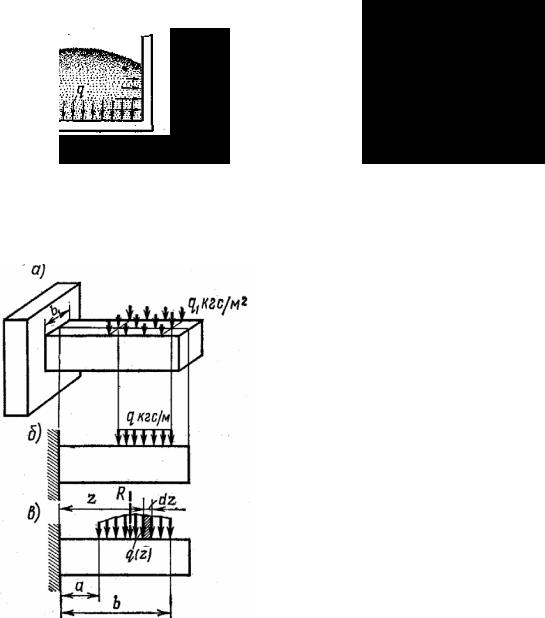
Рис. 1.4

Интенсивность нагрузки на единицу длины определяется произведением интенсивности распределенной нагрузки q1 на ширину балки b1:

q = q1b1

и поэтому измеряется в единицах силы, отнесенной к единице длины, например, тс/м или кгс/м и т. п. На рис. 1.5, б показана равномерно распределенная нагрузка q, a на рис. 1.5, в приведена неравномерная нагрузка q(z). Равнодействующая распределенной по какому-либо закону нагрузки определяется как сумма элементарных сил q(z)dz, действующих на отрезки dz:

b

R = ∫q(z)dz.

a

Приведенное выражение показывает, что равнодействующая распределенной нагрузки равна площади, ограниченной кривой, изображающей нагрузку q(z), и балкой, к которой она при-

ложена. Момент распределенной нагрузки относительно какой-либо точки определяется так же, как сумма моментов элементарных сил. Так, например, момент относительно заделки для случая, показанного на рис. 1.5, в, определится с помощью интеграла

b

M = ∫q(z)zdz.

a

Кроме этого, встречается нагрузка в виде сосредоточенных (рис. 1.6, а) или распределенных по длине пар сил (рис. 1.6, б). В последнем случае ин-

12

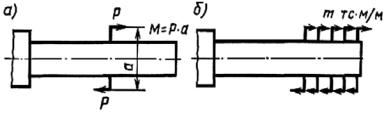
тенсивность нагрузки определяется величиной момента, приходящегося на единицу длины, а суммарный момент находится интегрированием:

M= ∫m(z)dz .

Взависимости от характера изменения нагрузок во времени их разделяют на статические и динамические. Статическая нагрузка прикладывается во времени настолько медленно, что ускорениями точек конструкции при их перемещениях, а, следовательно, и силами инерции, которые возникают при движении, можно пренебречь.

Рис. 1.6

Динамическая нагрузка в отличие от статической меняет свою величину или положение (движущаяся нагрузка) в сравнительно короткий промежуток времени.

По продолжительности действия на сооружение различают также постоянную и временную нагрузки. Постоянной называется нагрузка, которая действует непрерывно в течение всего срока службы сооружения, например, собственный вес конструкции. Временная нагрузка имеет ограниченную продолжительность действия, например, давление поезда на мост, вес снега и т. п.

Выше рассматривались силы, приложенные на поверхности тела, т. е. поверхностные силы. Наряду с этим встречаются объемные силы, распределенные по всему объему тела. К ним относятся собственный вес тела, силы магнитного притяжения, силы инерции и т. п.

При расчете реальных объектов приходится определять величины нагрузок от снега, ветра и т. п. Нагрузки такого типа имеют случайную природу. Они зависят от местоположения сооружения, рельефа местности, конструкции и очертания самого сооружения и т. п.

В строительных конструкциях объекты по геометрическим соображениям разделяют на ряд типов. На рис. 1.7, а показано массивное тело, у которого все основные размеры одного и того же порядка. К числу таких тел относятся, например, массивные фундаменты под колоннами зданий или под опорами контактной сети и т. п.

13

Рис. 1.7

На рис. 1.7, б показана пластина, отличающаяся тем, что толщина ее мала по сравнению с двумя другими размерами.

Наряду с пластинами встречаются оболочки (рис. 1.7, в), внешние контуры которых образованы не плоскостями, а криволинейными поверхностями. Толщинаоболочкималапосравнениюсеегенеральнымиразмерами.

Большое место в строительстве занимают стержни (брусья) прямолинейные (рис. 1.7, г) и криволинейные (рис. 1.7, д). Среди стержней в свою очередь различают балки, колонны, стойки и др. Это подразделение связано главным образом с назначением стержней и той ролью, которую они играют в конструкциях. Например, понятие «балка» употребляется для стержней, работающих на изгиб, понятие «колонна и стойка» – для вертикальных стержней, работающих преимущественно на сжатие, и т. д.

В сопротивлении материалов главное внимание уделяется расчету стержней, которые имеют очень большое распространение в строительной практике. Основными геометрическими элементами стержня являются его ось и поперечное сечение. Эти элементы взаимно связаны между собой. Ось представляет собой линию, проходящую через стороны, поперечными сечениями являются сечения, образованные плоскостями, проведенными перпендикулярно оси стержня. Стержень можно представить себе как тело, образованное плоской фигурой, движущейся по некоторой кривой таким об-

разом, что центр тяжести этой фигуры совпадает с кривой, а плоскость фигуры все время остается перпендикулярной к касательной, проведенной в соответствующей точке к данной кривой. В этом случае кривая является осью, плоская фигура – поперечным сечением стержня. На рис. 1.8 показан криволинейный стержень с осью

14

ABCD, а поперечные сечения в точках А, В, С и D – заштрихованные плоские фигуры.

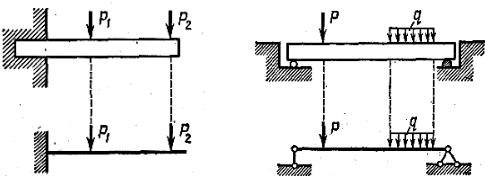
Стержни могут иметь постоянное или переменное сечение по длине. Для того чтобы произвести расчет какого-либо сооружения, сначала необходимо составить так называемую расчетную схему и уже для нее производить все необходимые вычисления. Так, на рис. 1.9 показаны две реальные балки и соответствующие им расчетные схемы.

Рис. 1.9

Схематически каждая балка изображается в виде одной осевой линии с идеализированными опорами. При составлении расчетных схем допускаются некоторые отступления от действительных условий работы конструкции. Считается, например, что свободно лежащая балка закреплена на концах шарнирами, в которых нет трения. Обычно считается, что нагрузка, действующая на балку, передается на ось, поэтому точки приложения нагрузки в расчетной схеме определяются, как показано на рис. 1.9.

При составлении расчетных схем необходимо иметь в виду, что некоторые правила теоретической механики применять нельзя. Так обстоит дело с переносом сил по линии их действия и с заменой сил их равнодействующей. Поясним это на примерах. На рис. 1.10, а показан стержень с силой, приложенной в точке А наверху. Если эту силу перенести по прямой в точку В (рис. 1.10, б), то равновесие стержня не нарушится, реакция в точках опоры не будет отличаться, но зато работа стержня резко изменится. В первом случае на участке АС стержень испытывает сжатие, а нижняя часть стержня не нагружена. Во втором случае верхняя часть стержня не нагружена, а нижняя часть испытывает растяжение. Перенос силы по линии ее действия резко изменил характер работы стержня и поэтому является недопустимым.

Приведем второй пример. Изучая равновесие тела, можно группу приложенных сил заменять ее равнодействующей и, наоборот, равнодействующую можно разлагать на составляющие. Если речь идет об определении перемещений, то этого делать нельзя. Так, например, на рис. 1.11, а показана балка с тремя равными силами. Замена этих сил их равнодейст-

15

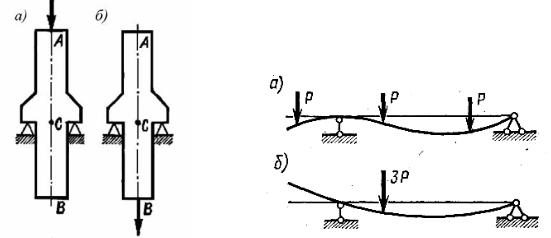
вующей, как это показано на рис. 1.11, б, резко изменяет форму изгиба балки, вместе с тем при определении опорных реакций такая замена в данном случае не приведет к ошибке.

1.3.Внутренние силы в стержне и их определение

Впроцессе деформации стержня под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего

внем изменяются внутренние силы. По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для того чтобы выявить эти силы, надо применить метод сечений; мысленно рассечь стержень, находящийся

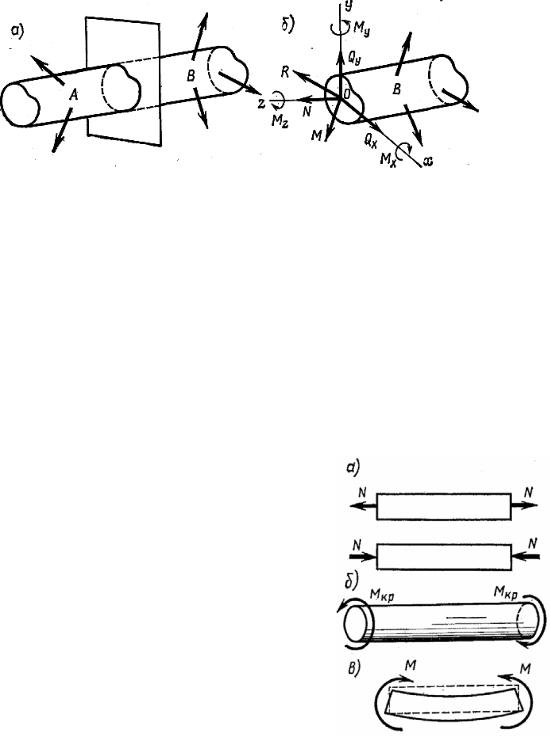
вравновесии, на две части и рассмотреть равновесие одной из них, например, части В (рис. 1.12, а).

Со стороны отброшенной части на часть В действует система внутренних сил, распределенных по всему сечению. Эту систему в общем случае можно привести к одной силе R (главному вектору) и к одной паре М (главному моменту).

При изучении внутренних сил в стержнях рекомендуется проводить сечение перпендикулярно оси стержня. Выберем оси координат х, у, z с началом в центре тяжести сечения так, чтобы оси Оу и Ох лежали в его плоскости. Разложим главный вектор на три составляющие по осям координат:

N, Qx, Qy, а главный момент М – на три момента: Мх, Му, Мz (рис. 1.12, б). Полученные таким образом величины представляют собой компо-

ненты внутренних сил, которые принято называть внутренними силовыми факторами, или просто внутренними силами. Каждая из этих сил имеет свое название: силу N, приложенную перпендикулярно сечению, называют нормальной силой; силы Qx и Qy, перпендикулярные оси стержня, называ-

16

ют поперечными силами. Моменты Мх и Му называют изгибающими, а Мz – крутящим моментом.

Учитывая, что деформации тела малы, считают отсеченную часть как бы затвердевшей: это позволит применить уравнения равновесия, известные из курса теоретической механики для абсолютно твердых тел.

Рис. 1.12

Чтобы вычислить указанные выше силовые факторы, достаточно написатьшестьуравненийравновесия, применяяихкоднойизотсеченных частей;

Из уравнений проекций соответственно могут быть вычислены силы N, Qx и Qy. Для определения изгибающих и крутящего моментов используются три последние уравнения.

При сложных нагрузках, действующих на стержень, в его поперечных сечениях могут одновременно возникнуть все шесть компонентов внутренних сил. В сопротивлении материалов изучение работы стержня под нагрузкой начинается с простейших случаев действия сил (рис. 1.13).

Если внешние силы, действующие на отсеченную часть стержня, приводятся к равнодействующей, направленной вдоль оси стержня, то в поперечном сечении возникнет только нормальная сила N, a остальные внутренние силы будут равны нулю. В таком случае возникает растяжение или сжатие (рис. 1.13, а), при котором стержень удлиняется или укорачивается, а его ось остается прямой.

17

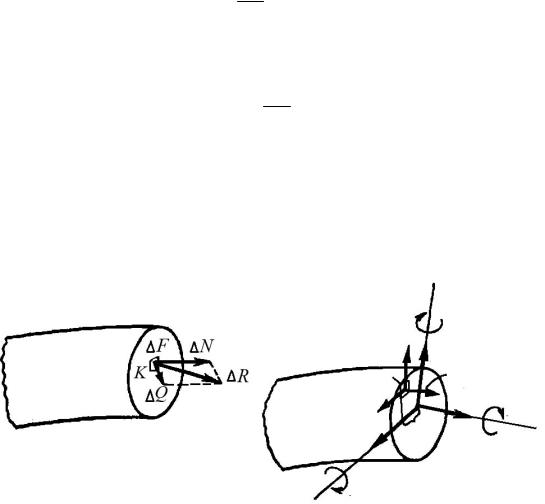
На рис. 1.13, б показан случай кручения, при котором в поперечных сечениях возникают только крутящие моменты. При кручении ось стержня также остается прямой, а поперечные сечения поворачиваются вокруг оси стержня относительно друг друга на некоторый угол.

На рис. 1.13, в показан случай так называемого чистого изгиба, при котором во всех сечениях стержня возникает только изгибающий момент, а ось стержня искривляется.

1.4. Понятие о напряжениях и деформациях в точке

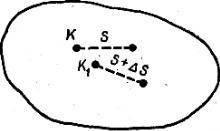
На основании сделанных ранее допущений о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению. Выделим в произвольной точке К малую площадку ∆F, а равнодействующую внутренних сил на этой площадке обозначим ∆R (рис. 1.14, а). Отношение

∆∆FR = pср

представляет собой среднее напряжение на данной площадке. Если площадку ∆F уменьшать, то в пределе получим напряжение в точке

lim ∆R = p.

∆F →0 ∆F

Если силу ∆R разложить на две составляющие: нормальную ∆N и касательную ∆Q, то по ним можно определить нормальное и касательное напряжения:

Рис. 1.14

18

Напряжения являются мерой интенсивности внутренних сил и

измеряются в единицах силы, отнесенной к единице площади, например, кгс/см2, кгс/мм2, тс/м2 и т. п.

Касательное напряжение имеет различные направления, поэтому удобнее вместо одного определять два касательных напряжения: τx и τy направленных вдоль осей Ох и Оу.

Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dF и приложим к ней элементарные силы σdF, τydF, τxdF (рис. 1.14, б).

Интегрирование проводится по всей площади поперечного сечения, что позволяет определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению. Заметим, что обратную задачу с помощью только одних указанных уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например, N могут соответствовать различные законы распределения нормальных напряжений по сечению.

Одной из основных задач сопротивления материалов является задача определения напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформаций бруса.

Для определения деформаций в точке К рассмотрим малый отрезок s, исходящий из этой точки в произвольном направлении

(рис. 1.15). В результате деформации точка К сместится в точку К1, а отрезок s удлинится на величину ∆s и изменит свое направление.

Предел отношения

lim ∆ss = ε

носит название относительной линейной деформации в точке К по направ-

лению s. Если в точке К провести три оси, параллельные осям координат Ох, Оу, Оz, то линейные деформации в направлении этих осей соответственно равны εx, εy, εz. Вследствие деформации первоначально прямые углы между малыми отрезками dx, dy, dz, исходящими из точки K, изменятся на малые углы yxy, yxz, ууz. Эти изменения прямых углов называют угловыми деформациями в точке К. Таким образом, в любой точке имеют место три линейных и три угловых компонента деформации.

19

М-2. РАСТЯЖЕНИЕ И СЖАТИЕ

2.0. Введение в модуль

Модуль содержит следующие структурные элементы:

1.Продольные силы и их эпюры.

2.Напряжения и деформации при растяжении и сжатии.

3.Влияние способа приложения внешней нагрузки.

4.Диаграмма растяжения.

5.Проверка прочности при растяжении.

Цель модуля – изучение методики расчета прочности и определения перемещений и деформаций при растяжении и сжатии.

2.1. Продольные силы и их эпюры

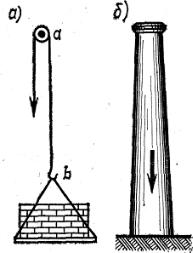
Растяжение и сжатие весьма часто встречаются в элементах строительных конструкций и машин. Например, растяжение возникает в тросе аb подъемника (рис. 2.1, а), в буксировочном тросе (при буксировке автомобиля), сжатие возникает в фабричной трубе (рис. 2.1, б) от ее собственного веса, в колоннах, поддерживающих перекрытия, и т. п.

Если внутренние силы в поперечном сечении стержня сводятся только к одному силовому фактору – продольной силе N (иначе называемой нормальной силой, так как она перпендикулярна поперечному сечению стержня), а все остальные внутренние силы равны нулю, то имеет место чистое (центральное) растяжение или сжатие.

Для определения продольных сил применяется метод сечений, который заключается в том, что стержень мысленно рассекается плоскостью, перпендикулярной оси стержня, на две части.

Взаимодействие частей между собой заменяется продольной силой N и из условия равновесия какой-либо из двух частей определяется значение этой силы.

Условимся силу N считать положительной, если она вызывает растяжение (направлена от сечения), и отрицательной, если она вызывает сжатие (направлена к сечению).

В тех случаях, когда направление силы N неизвестно, целесообразно принять ее положительной. Если при решении уравнения равновесия сила N получится со знаком «+», то стержень в данном сечении будет растянут, если со знаком

20