- •Нелинейная механика грунтов
- •Дисперсные грунты крупнообломочные грунты
- •Физические характеристики грунтов
- •1.2. Формы расчётных областей, системы координат, правила знаков
- •1.3. Условия предельного напряженного состояния грунтов
- •Матрицы (1.10), (1.12), (1.13) связаны равенством
- •1.4. Зависимость между перемещениями, напряжениями и деформациями
- •1.5. Расчётные модели геотехнических систем
- •1.5.1. Упрощённые модели
- •Дифференциальные уравнения равновесия. Принцип Лагранжа, равновесие узлов системы мкэ Равновесие тела обрушения и его частей (отсеков). Предельное напряженное состояние в точке
- •Жёстко-пластическая среда
- •Задача Фламана Задача Буссинеска
- •Начальная критическая нагрузка на основание Метод горизонтальных сил г.М. Шахунянца
- •Метод угловых точек
- •1.5.2. Нелинейные модели грунта
- •Контрольные вопросы для самопроверки
- •2. Метод конечных элементов в механике грунтов
- •2.1. Теоретические основы мкэ. Идеи, постулаты
- •2.2. Матрицы жёсткости конечных элементов
- •2.2.1. Общие положения
- •2.2.2. Матрица жёсткости стержневого кэ
- •2.2.3. Функции перемещений континуальных конечных элементов
- •2.2.4. Построение матриц жёсткости континуальных кэ
- •1…16 – Номера степеней свободы
- •2.3. Глобальная матрица жёсткости системы
- •2.3.1. Общая и местная системы координат
- •2.3.2. Формирование систем уравнений
- •2.3.3. О решении системы уравнений
- •2.3.4. Завершающие процедуры статического расчёта
- •2.4. Специальные конечные элементы
- •2.5. Решения физически нелинейных задач средствами мкэ
- •2.6. Заключительные замечания. Ключевые положения мкэ
- •Контрольные вопросы для самопроверки
- •Равновесие узлов системы мкэ. Принцип Лагранжа
- •Уравнение
- •Мора - Кулона
- •Закон Кулона (для заданных поверхностей сдвига)
- •Уравнение Мизеса -
- •Шлейхера - Боткина
- •Закон Гука
- •Смешанная (упругопластическая) задача теорий упругости и пластичности
- •Плоская деформация Пространственная и осесимметричная задача
- •3.2. Программное обеспечение. Критерии предельных состояний
- •3.3. Примеры решения научно-технических задач1
- •Контрольные вопросы для самопроверки
- •Заключительные замечания
- •Библиографический список
- •Сведения из алгебры матриц
- •Понятия, определения
- •Действия с матрицами
- •Давид Моисеевич Шапиро нелинейная механика грунтов
- •3 94006 Воронеж, ул. 20-летия Октября, 84
1.4. Зависимость между перемещениями, напряжениями и деформациями
В настоящем параграфе рассматриваются условия деформирования грунтов (связи между перемещениями, напряжениями и относительными деформациями) с делением на стадии линейного деформирования и пластического течения (до и после достижения условия текучести в соответствии с уравнениями Мора-Кулона или Мизеса-Шлейхера-Боткина).
Соотношения Коши и обобщённый закон Гука. Напомним обозначения составляющих перемещений в точке U, W, V по направлениям осей X, Y, Z и введём обозначения деформаций: εx, εy, εz, γxy, γxz, γyz – относительные осевые и угловые деформации в прямоугольных координатах; ε1, ε2, ε3 – главные относительные деформации.
Линейные соотношения, связывающие перемещения, относительные деформации и напряжения, имеют следующий вид.
Соотношения Коши связи между перемещениями и деформациями (выражают непрерывность и относительную малость перемещений):
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
(1.22)
.
(1.22)
Напомним читателям происхождение указанных выше уравнений. С этой целью рассмотрим проекцию и перемещения на плоскости XOZ элементарного объёма упругого тела с размерами dx dy dz (рис. 16). В соответствии с изображением на рисунке абсолютные удлинения по направлениям X и Z соответственно равны (дU/дх)dx и (дV/дy)dy, а относительные удлинения (деформации)
 ;
;
 .
.
Изменение угла в плоскости XOZ (см. рис. 16):
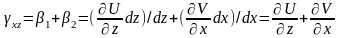 .
.
Аналогичным путём (при помощи проекций на плоскости XOY, YOZ) получим относительную деформацию εy и углы γxy, γyz.
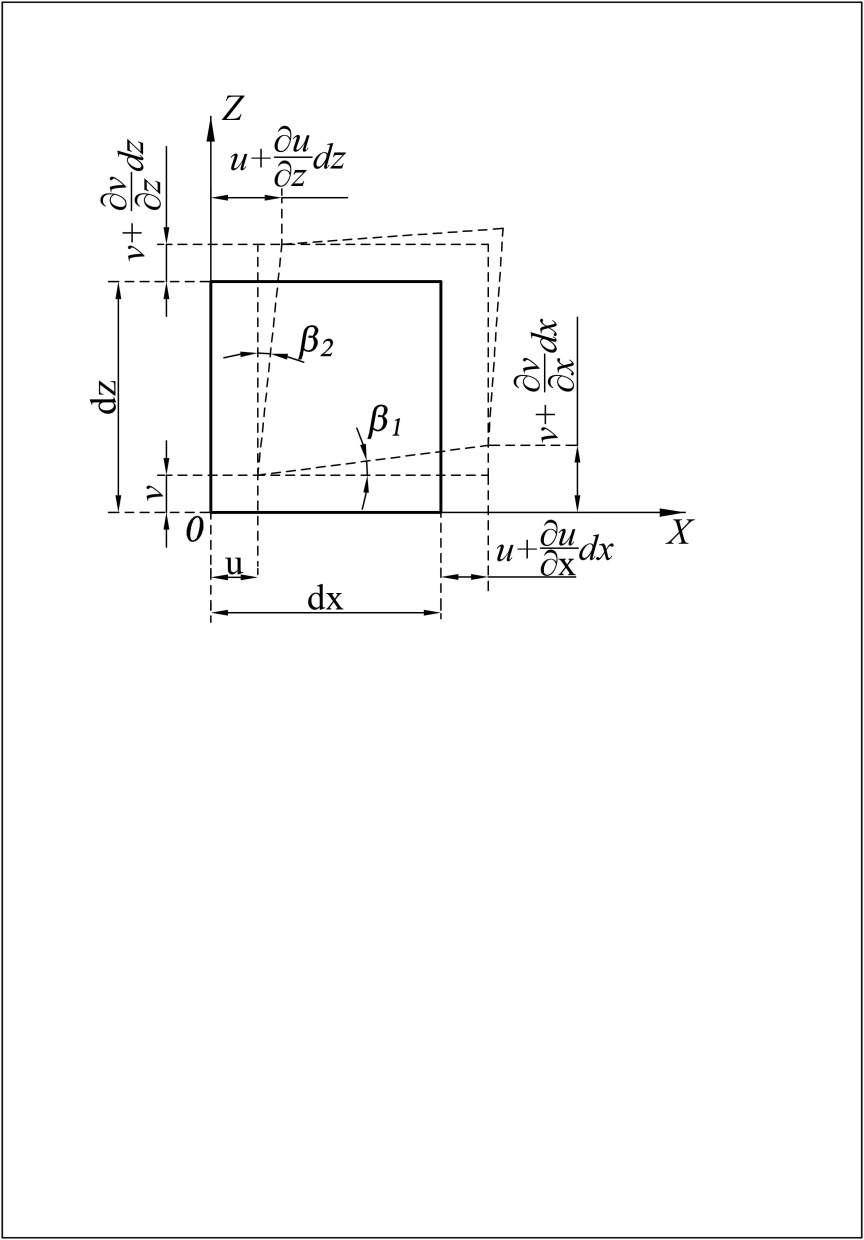
Рис. 16. Проекция и перемещения элементарного объёма упругого тела
Положительные направления εx, εy, εz соответствуют удлинению по соответствующим направлениям, а γxy, γxz, γyz – уменьшению углов.
Уравнения закона Гука для сплошных изотропных расчётных областей имеют следующий вид.
Плоская деформация:
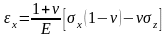 ,
,
 ,
,
 .
(1.23)
.
(1.23)
Пространственное напряженное состояние:

 ,
,
 ,
,
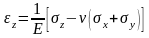 ,
(1.24)
,
(1.24)
 ,
,
 ,
,
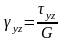 .
.
В
уравнениях (1.23) и (1.24) обозначено:
 –модуль
деформации,
–модуль
деформации,
 –
коэффициент Пуассона (поперечной
деформации),
–
коэффициент Пуассона (поперечной
деформации),
 – модуль сдвига.
– модуль сдвига.
Продолжим рассмотрение тех же постулатов применительно к условиям осесимметричного напряжённого состояния и деформирования (рис. 17), принимая следующие обозначения: U, V – составляющие перемещений в точке в направлениях радиальной X и вертикальной Z осей; εx, εz, εθ, σx, σz, σθ – относительные деформации и напряжения в радиальном, вертикальном и тангенциальном направлениях; γxz, τxz – угловые деформации и касательные напряжения в плоскости XOZ; ε1, ε2, ε3, σ1, σ2, σ3 – главные относительные деформации и напряжения.
|
Рис. 17. Схема осесимметричного напряженного состояния
|
Соотношения Коши и уравнения закона Гука:
,
,
 ,
;
(1.25)
,
;
(1.25)
 ,
,
 ,
,
 ,
.
(1.26)
,
.
(1.26)
Инварианты относительных деформаций. При анализе результатов экспериментов и постановке задач строгой теории используются инварианты деформаций, подобные инвариантам тензора напряжений I1, I2: первый инвариант J1 тензора деформаций, равный объёмной деформации εv:
J1= εv=ε1+ ε2+ ε3= εx+εy+εz; (1.27)
второй инвариант девиатора деформаций:
J2
= [(ε1−ε2)2+(ε2−ε3)2+(ε3−ε1)2]=
[(ε1−ε2)2+(ε2−ε3)2+(ε3−ε1)2]=
= [(εx−εy)2+(εy−εz)2+(εz−εx)2+1.5(γxy2+γyz2+γxz2)]; (1.28)
интенсивности линейных εi и угловых γi деформаций:
 ;
;
 .
(1.29)
.
(1.29)
Характеристики деформируемости грунтов. В рассматриваемых ниже расчётных моделях используются три деформационные характеристики грунтов: модуль деформации Е, модуль упругости Ее и коэффициент поперечной деформации (коэффициент Пуассона) ν. Различие между модулями Е и Ее заключается в том, что первый из них отражает полную деформацию, состоящую из линейной и нелинейной (обратимой и необратимой) составляющих на допредельной стадии деформирования, второй отражает только упругую (восстанавливающуюся) часть деформаций, которая фиксируется при снятии и повторном приложении нагрузки.
Назначение деформационных характеристик относится к числу наиболее ответственных решений при проектировании, особенно в сочетании с численными методами, ведущими к расширению области использования деформационных расчётов. Существуют многочисленные таблицы (в том числе в приложении Б СП 22.13330.2011), связывающие модули деформации Е с физическими характеристиками грунтов. Табличные данные используются на практике в связи с ограниченными возможностями проведения специализированных инженерно-геологических изысканий при проектировании объектов средней технической сложности. В указанном нормативном документе предусмотрена возможность упрощённого назначения модуля упругости по соотношению Ее=5Е.
Для коэффициентов ν также существуют табличные значения, последний вариант которых содержится в табл. 5 , повторяющей данные СП 22.13330.2011, табл. 5.10.
Таблица 5
Коэффициенты поперечной деформации
Грунты |
Коэффициенты поперечной деформации ν |
Крупнообломочные грунты |
0,27 |
Пески и супеси |
0,30−0,35 |
Суглинки |
0,35−0,37 |
Глины при показателе текучести IL≤0 0< IL≤0,25 0,25< IL≤1 |
0,20−0,30 0,30−0,38 0,38−0,45 |
Табличные данные в нормативно-методических документах отражают обширный эмпирический материал, основанный на полевых и лабораторных измерениях. Знание схем и способов проведения различных видов испытаний позволяет лучше понимать физическое содержание рассматриваемых характеристик, учитывать погрешности их измерений.
Одним из способов лабораторного определения деформационных характеристик является рассмотренный выше метод трёхосного сжатия образцов грунта по версии консолидированно-дренированного испытания. Модуль деформации и коэффициент поперечной деформации в опыте при постоянном значении напряжений σ1,2 определяются по формулам
 ,
,
 ,
(1.30)
,
(1.30)
где
Δσ3
– приращение напряжений σ3
в заданном диапазоне;
 ,
,
 ,
,
 – приращение
относительной вертикальной, поперечной
и объёмной деформаций образца; Δh,
ΔV
– абсолютные
вертикальная и объёмная деформации
образца грунта с учётом поправки на
сжатие камеры, h,
V
– начальные
высота и объём образца.
– приращение
относительной вертикальной, поперечной
и объёмной деформаций образца; Δh,
ΔV
– абсолютные
вертикальная и объёмная деформации
образца грунта с учётом поправки на
сжатие камеры, h,
V
– начальные
высота и объём образца.
Другими известными способами определения Е и ν являются следующие эксперименты. Лабораторные испытания: компрессионные, одноосные. Полевые измерения: штамповые, прессиометрические испытания, статическое и динамическое зондирование. Их описание не относится к задачам настоящего издания.
Фазы напряжённого состояния грунтов. Диаграмма Прандтля. В теории механики грунтов принято выделять две фазы напряжённо-деформированного состояния грунта: 1) фазу уплотнения и локальных сдвигов; 2) фазу значительных сдвигов.
Первая фаза характеризуется преобладанием деформаций уплотнения, близкой к линейной зависимостью между напряжениями и деформациями, быстрым затуханием деформаций. Если оценивать напряжённое состояние грунта в соответствии с условиями текучести Мора-Кулона и Мизеса-Шлейхера-Боткина, то на данной стадии площадки сдвига (пластические области) только зарождаются либо не образуются вообще. Состояние грунта оценивается как допредельное.
При возрастании величины и неравномерности нагрузки площадки скольжения соединяются, образуя развитые поверхности. Грунт переходит в близкое к предельному состояние, которому присущи разрывы сплошности или образование обширных пластических областей с нелинейной связью между напряжениями и деформациями. Такое напряжённое состояние, если оно приближается к исчерпанию несущей способности или характеризуется прогрессирующей текучестью, является недопустимым.
При проектировании (расчётах) геотехнических объектов с использованием в качестве теоретической основы законов Гука, Кулона, уравнений Мора-Кулона, Мизеса-Шлейхера-Боткина принимается билинейная зависимость ε=f(σ), известная в теории как диаграмма Прандтля (рис. 18), позволяющая получить качественно верную, удовлетворяющую практическим требованиям картину напряжённо-деформированного состояния. Точка А на билинейной диаграмме изображает предел текучести. Условия деформирования грунта на наклонном и горизонтальном участках билинейной диаграммы качественно отличаются и описываются разными уравнениями.
Для наклонного участка ОА принимается модель линейно-деформируемого тела, описываемая обобщённым законом Гука и характеризуемая модулем деформации Е и коэффициентом Пуассона ν.
|
Рис. 18. Двухмерная
аналогия зависимостей
|
В соответствии с уравнениями закона Гука направления векторов главных напряжений (σ1,2) и главных относительных деформаций (ε1.2) совпадают или (в терминах теории деформируемых тел) соосны, коаксиальны. Объёмная деформация в теле Гука
εv=εx+εy+εz= (σx+σy+σz)=
(σ1+σ2+σ3).
(1.31)
(σx+σy+σz)=
(σ1+σ2+σ3).
(1.31)
Девиатор напряжений {σ1–σm σ2–σm σ3–σm} не воздействует на объёмную деформацию.
Достижение предела текучести связано с наступлением предельного напряжённого состояния грунта в соответствии с уравнениями Мора-Кулона или Мизеса-Шлейхера-Боткина. На горизонтальном участке диаграммы ОАВ численные значения деформаций (перемещений) не определяются, а их векторы описываются соотношениями теории пластичности, которые рассматриваются ниже.
Понятие о векторах пластических деформаций. Дилатансия. При решении смешанных задач теории упругости и пластичности требуется расчётное описание вектора относительных деформаций на ветви АВ (см. рис. 18) диаграммы Прандтля. При этом рассматриваются два вопроса: об ориентации осей тензора-девиатора деформаций и о влиянии формоизменения на объёмное деформирование.
На стадии пластического течения векторы главных напряжений и деформаций так же, как и на упругой стадии, принимаются соосными. Однако в этом случае рассматриваемое положение вводится не как следствие физических уравнений, а в качестве самостоятельного допущения, основанного на экспериментальных данных или полученного при помощи соотношений теории пластического течения.
Изложенные выше положения позволяют считать соосными векторы главных напряжений, линейных и пластических составляющих главных деформаций на всех стадиях деформирования элементарного объёма (точки) грунтовой среды.
Ещё одним положением теории деформирования на стадии пластического формоизменения является наличие дилатансии, т. е. изменения (как правило, увеличения, «разрыхления») объёма. Явление дилатансии при сдвиге грунтов зафиксировано во многих экспериментах и объясняется как следствие изменения взаимного положения («переупаковки») частиц грунта при формоизменении.
Пластическое деформирование элементарного объёма грунта в условиях плоской деформации происходит в соответствии со схемой на рис. 18 по уравнению
 ,
(1.32)
,
(1.32)
где ε1,2р – пластические составляющие главных деформаций; λ – малая скалярная величина; Λ* – параметр дилатансии, константа, отражающая изменение объёма при формоизменении (сдвиге) грунта в условиях плоской деформации. Из уравнения (1.32) следует, что
 .
(1.33)
.
(1.33)
Наличие
коэффициента Λ*≠0
отличает
деформацию в соответствии с уравнением
(1.32) от течения при постоянном объёме,
где ε1,2p=± ,
а на площадках, наклонённых под углом
450
по отношению к осям главных напряжений,
имеет место εpπ/4=0,
γрπ/4=
,
а на площадках, наклонённых под углом
450
по отношению к осям главных напряжений,
имеет место εpπ/4=0,
γрπ/4= (ε1р
– ε2р)
=
.
(ε1р
– ε2р)
=
.
|
Рис. 19. Формоизменение и дилатансия элементарного объема грунта при пластическом деформировании: 1 – первоначальные размеры; 2 – сдвиг при постоянном объеме (Λ*=0); 3 – формоизменение с дилатансией (Λ*>0)
|
Ассоциированный
и неассоциированный законы течения.
Теория пластического течения связывает
поле скоростей (приращений) пластических
деформаций
 с частными производными некоторой
функции F=0,
называемой пластическим потенциалом:
с частными производными некоторой
функции F=0,
называемой пластическим потенциалом:
 ,
(1.34)
,
(1.34)
где λ – неопределённый положительный коэффициент пропор-циональности, малая скалярная величина. Пластический потенциал F(σij)=0 описывает в п-мерном пространстве напряжений некоторую поверхность. Математически зависимость (1.34) означает перпендикулярность вектора приращений (скоростей) пластических деформаций к линии или поверхности F=0.
В частном случае, если в качестве пластического потенциала принять уравнение текучести (1.7) или (1.20) F =Fр=0, соотношение
 (1.35)
(1.35)
будет выражать ассоциированный закон течения. Данный термин связан с общей (ассоциированной) записью зависимостей, определяющих предельное напряжённое состояние и вектор пластического течения.
Уравнениям пластических потенциалов
 ,
,

можно придать более общий вид путём подстановки вместо sinφ и α параметров дилатансии Λ*, Λ, определяемых экспериментальным путём, выражающих линейную связь объёмных деформаций и формоизменения в условиях плоской деформации и пространственного напряжённого состояния. Новые соотношения [3]
 ,
(1.36)
,
(1.36)
 (1.37)
(1.37)
описывают пластические потенциалы неассоциированного закона течения.
Из уравнений (1.34)–(1.37) следуют важные в практическом отношении зависимости. При F=0, определяемом уравнением (1.36), в условиях плоской деформации
 ;
;
 .
(1.38)
.
(1.38)
Обратим внимание на то, что соотношения последней строки повторяют приведенные выше уравнения (1.32), (1.33) с графической иллюстрацией на рис. 19.
Графической формой уравнений (1.32)–(1.38) являются диаграммы на рис. 20, изображающие пластические потенциалы Fр=0 и F=0 и векторы ассоциированного и неассоциированного законов течения на плоскости главных напряжений σ1, σ2.
|
Рис. 20. Пластические потенциалы неассоциированного (ассоциированного) законов течения 1(2) и соответствующие им векторы пластических деформаций 3(4) |
При F=0 в соответствии с (1.37) в условиях пространственной задачи
 .
(1.39)
.
(1.39)
В соответствии с последним уравнением объёмная пластическая деформация Jр1=εр1+εр2+εр3=3λΛ, а выражение
 .
.
Откуда следует
 .
(1.40)
.
(1.40)
В научной литературе и некоторых программах расчётов геотехнических объектов используется термин «угол дилатансии», связывающий объёмную деформацию при сдвиге с деформацией сдвига ψ=arc tg Λ* (или Λ).
Следствием изложенного выше являются следующие кинематические свойства рассматриваемой модели:
– тензоры-девиаторы скоростей пластических деформаций и напряжений соосны (коаксиальны);
– пластические деформации формоизменения должны сопровождаться относительным увеличением объёма со скоростью λΛ* или 3λΛ.
Указанные выше положения подтверждаются большинством экспериментов, и их практическое использование можно считать пригодным для прикладных задач. Обобщение большого числа опытных исследований (А. К. Бугров, 19801) позволило сделать вывод о том, что относительное увеличение объёма, сопровождающее формоизменение, меньше или близко к значениям ассоциированного закона: в экспериментах с плотными грунтами Λ*=(0.87÷1.00)sinφ, а в опытах с грунтами рыхлыми и средней плотности Λ*=(0.30÷0.50)sinφ.
Модель Друккера-Прагера в соответствии с описанием в статье [9] является версией модели Мизеса-Шлейхера-Боткина со следующими особенностями.
В качестве условия текучести принято уравнение (1.20)
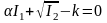 .
(а)
.
(а)
Описание деформирования после достижения предела текучести в соответствии с ассоциированным законом течения:
или
 ,
(б)
,
(б)
где
I1=σх+σz+σy=σ1+σ2+σ3, (в)
I2= [(σх–σz)2+(σz–σy)2+ (σy–σx)2]+τxz2+ τxy2+τyz2 (г)
– первый инвариант тензора и второй инвариант девиатора напряжений в точке (элементарном объёме) грунта.
В условиях плоской деформации τxy=τyz=0. Требуется, чтобы третья (нормальная к расчётной плоскости) главная деформация ε3=εу равнялась нулю, и грунт одновременно удовлетворял уравнению (а)–(1.17) и условию текучести Мора-Кулона (1.7):
 .
(д)
.
(д)
Основываясь на этих соображениях, можно сделать следующие записи:
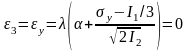 ;
(1.41)
;
(1.41)
 ;
(1.42)
;
(1.42)
 ;
;
 ;
;
 ;
(1.43)
;
(1.43)
 .
(1.44)
.
(1.44)
Подстановка (1.44) в уравнение (г) после некоторых преобразований позволяет получить

 .
.
Из последнего уравнения следует:

или
 .
(1.45)
.
(1.45)
Подстановка (1.42) в уравнение (а)–(1.20) Fp=0 позволяет получить
Fp=3α[½(σx+σz)]+(1–3α2) –k=0.
(1.46)
–k=0.
(1.46)
Заменяя в последнем выражении правой частью уравнения (1.45), получаем
 .
(1.47)
.
(1.47)
Уравнение (1.47) является одновременно тождественной формой выражений (а)–(1.20) и (д)–(1.7) при условиях
 ,
,
 ,
,
 .
.
Если
приближённо принять
 ,
можно получить простые соотношения
связи между парами прочностных
характеристик α,
k
и φ,
с
,
можно получить простые соотношения
связи между парами прочностных
характеристик α,
k
и φ,
с
 ,
,
 .
(1.48)
.
(1.48)
О сопротивлении грунта растяжению. При проектировании, а также реальном поведении сооружений возможны условия, когда на некоторой части грунтового массива возникает растяжение. Грунты слабо сопротивляются растягивающим напряжениям, в зонах их действия образуются трещины, отрыв поверхностей фундаментных конструкций от основания (например, при воздействии на сваю горизонтальной силы). В расчётах обычно принимается, что грунт работает только на сжатие, не воспринимает растягивающие напряжения, деформируется при их воздействии без сопротивления. Важным аргументом в пользу такого допущения является соображение о том, что даже в тех случаях, когда растягивающие напряжения незначительны и не вызывают разрывов, теряет силу закон внутреннего трения и модуль деформации значительно ниже, чем при сжатии.

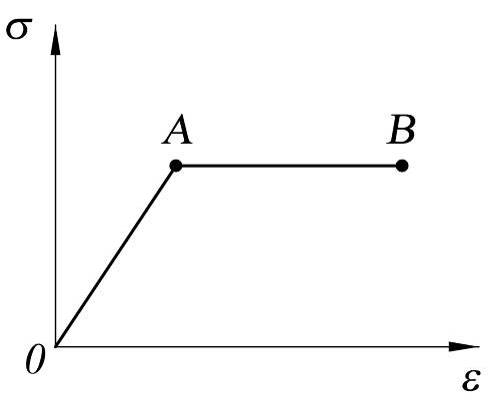
 к модели упругопластического тела в
соответствии с диаграммой Прандтля
к модели упругопластического тела в
соответствии с диаграммой Прандтля