2.2.4. Построение матриц жёсткости континуальных кэ

Треугольный КЭ. Общий вид связи между узловыми перемещениями и силами в вершинах треугольника на рис. 27, б представляет собой матричное соотношение

{F}=[K]{U}, (2.10)

подобное (2.1), где {F} и {U} по-прежнему векторы-столбцы сил и перемещений в узлах КЭ:

, , (2.11)

[K] – матрица жёсткости, подобная (2.4), которую необходимо построить.

Условно принимается, что в матричном соотношении (2.10) силы {F} неизвестны, а шесть перемещений {U} узлов заданы.

Исходными соотношениями для решения поставленной задачи (определения коэффициентов K_ij, формирующих матрицу [K]) являются соотношения Коши (1.19), уравнения закона Гука (табл. 7) и координатные функции (2.5) с коэффициентами α_k (k=1…6) в соответствии с уравнениями (2.7).

Построение уравнений связи между известными перемещениями {U} и неизвестными силами {F} осуществляется в три этапа.

1. Определение относительных деформаций. Подстановка функций (2.5) в дифференциальные соотношения Коши (1.19) позволяет получить следующие значения относительных деформаций ε_х, ε_z, γ_xz:

; ; , (2.12)

где α₂, α₃, α₅, α₆ – коэффициенты в соответствии с (2.7).

Соотношения между столбцами деформаций и {U} могут быть представлены в матричной форме:

{ε}=[В]{U}, (2.13)

где

(2.14)

− матрица соотношений Коши. Размерность матрицы [B] м^–1.

2.Переход от деформаций к компонентам напряжений. Относительные деформации связаны с напряжениями σ_х, σ_z, τ_xz уравнениями закона Гука:

или , {σ}=[D] [В]{U}, (2.15)

где [D] – матрица закона Гука из табл. 7 для плоской деформации.

Рассмотрим уравнения (2.5), (2.7) и (2.12) – (2.15). Перемещения u, v являются линейными функциями координат, относительные деформации {ε}, как первые производные перемещений, постоянны на всей площади треугольника. Компоненты напряжений, связанные с деформациями матрицей констант [D], также не изменяются от точки к точке, т. е. являются постоянными в пределах треугольного КЭ.

3.Определение узловых сил по известным напряжениям. Заключительный этап построения матрицы жёсткости КЭ связан с получением уравнений связи между матрицами-столбцами напряжений {σ} и узловых сил {F}. В связи с невозможностью реализовать обычные условия равновесия при построении матриц жёсткости континуальных КЭ используется принцип Лагранжа минимума потенциальной энергии системы. В МКЭ использование принципа Лагранжа выражается в виде следующего матричного соотношения, которое (применительно к плоским системам) записывается без вывода:

{F} = t∫∫_S [В]^Т{σ}dS, (2.16)

где t=1 м – толщина КЭ в условиях плоской деформации, S – площадь КЭ, [В]^Т – транспонированная матрица [В] со следующей записью:

. (2.17)

Для треугольного КЭ с постоянными напряжениями на всей площади треугольника ∫∫_SdS=S выражение (2.17) принимает вид

{F} = St [В]^Т{σ}. (2.18)

В развёрнутой записи соотношения (2.18) имеют следующий вид:

, ,

, ,

, .

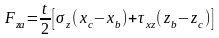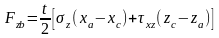В окончательном виде матричное соотношение между узловыми силами и перемещениями узлов треугольника представляет собой следующее выражение:

{F} = St [В]^Т [D] [В] {U}=[K]{U}, (2.19)

где

[K]= St [В]^Т [D] [В] − (2.20)

− матрица жёсткости треугольного КЭ.

В развёрнутой записи матрица (2.20) имеет следующий вид:

(2.21)

В матричном выражении (2.21) приняты следующие обозначения: x_ab=x_a−x_b, x_bc=x_b−x_c, x_ac=x_a−x_c, z_ab=z_a−z_b, z_bc=z_b−z_c, z_ac=z_a−z_c; A, B, C, G=E/2(1+ν) – коэффициенты, включающие параметры закона Гука. Для плоской деформации

, , . (2.22)

Размерность коэффициентов K_ij – Нм^-1, кНм^-1.

Четырёхузловой прямоугольный КЭ. Исходной базой для построения матрицы жёсткости прямоугольного КЭ является схема на рис. 27, в и уравнения (2.8) функций перемещений с коэффициентами α₁…α₈ в соответствии с (2.9).

Для построения матрицы жёсткости необходимо получить соотношения [B], т. е. определить относительные деформации как частные производные уравнений (2.9) с подстановкой в них значений α_k (k =1…8):

(2.23)

где l и m – размеры сторон прямоугольника.

В матричной форме эти соотношения выглядят так:

; , ; (2.24)

, (2.25)

где − площадь КЭ.

Матрица [B] может быть представлена как матричное произведение:

[B]= [L] [Q], (2.26)

где

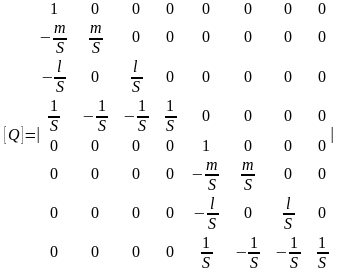, (2.27)

. (2.28)

Матрица [Q] выражает связи между столбцами {α} и {U} ({α}=[Q]{U}) в соответствии с (2.19) и включает только постоянные величины. Матрица [L] выражает связи между {ε} и {α} в соответствии с (2.23): {ε}= [L]{α}.

Транспонированная матрица [B] имеет вид:

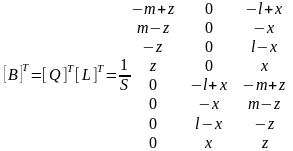(2.29)

Теперь не остаётся препятствий к тому, чтобы, руководствуясь соотношением (2.16), получить матрицу жёсткости четырёхузлового прямоугольного КЭ:

{F} = t∫∫_S [В]^Т{σ}dS= t∫∫_S [В]^Т [D] [В] {U}dS=[K]{U}, (2.30)

где

; (2.31)

, (2.32)

где А, В, С – жёсткостные характеристики в соответствии с (2.22) и G=E/2(1+ν).

Восьмиузловой прямоугольный КЭ. Выше было рассмотрено построение матриц жёсткости простейших плоских КЭ: треугольника и прямоугольника с шестью и восьмью степенями свободы. Продолжим построение матриц жёсткости на примере более сложного КЭ – восьмиузлового прямоугольника с 16^-ю степенями свободы в узлах. Покажем, что при любом уровне сложности КЭ процедура построения матрицы жёсткости остаётся одной и той же. Достаточно получить матрицу [B]=[L][Q], и последующий математический процесс состоит только из перемножения, транспонирования готовых матриц и интегрирования в соответствии со следующим выражением:

[K]=t∫∫_S[B]^T[D][B] dS = t∫∫_S[Q]^T [L]^T [D][L] [Q] dS. (2.33)

Запишем функции перемещений для восьмиузлового прямоугольника с 16^ю степенями свободы в узлах (рис. 29):

(2.34)

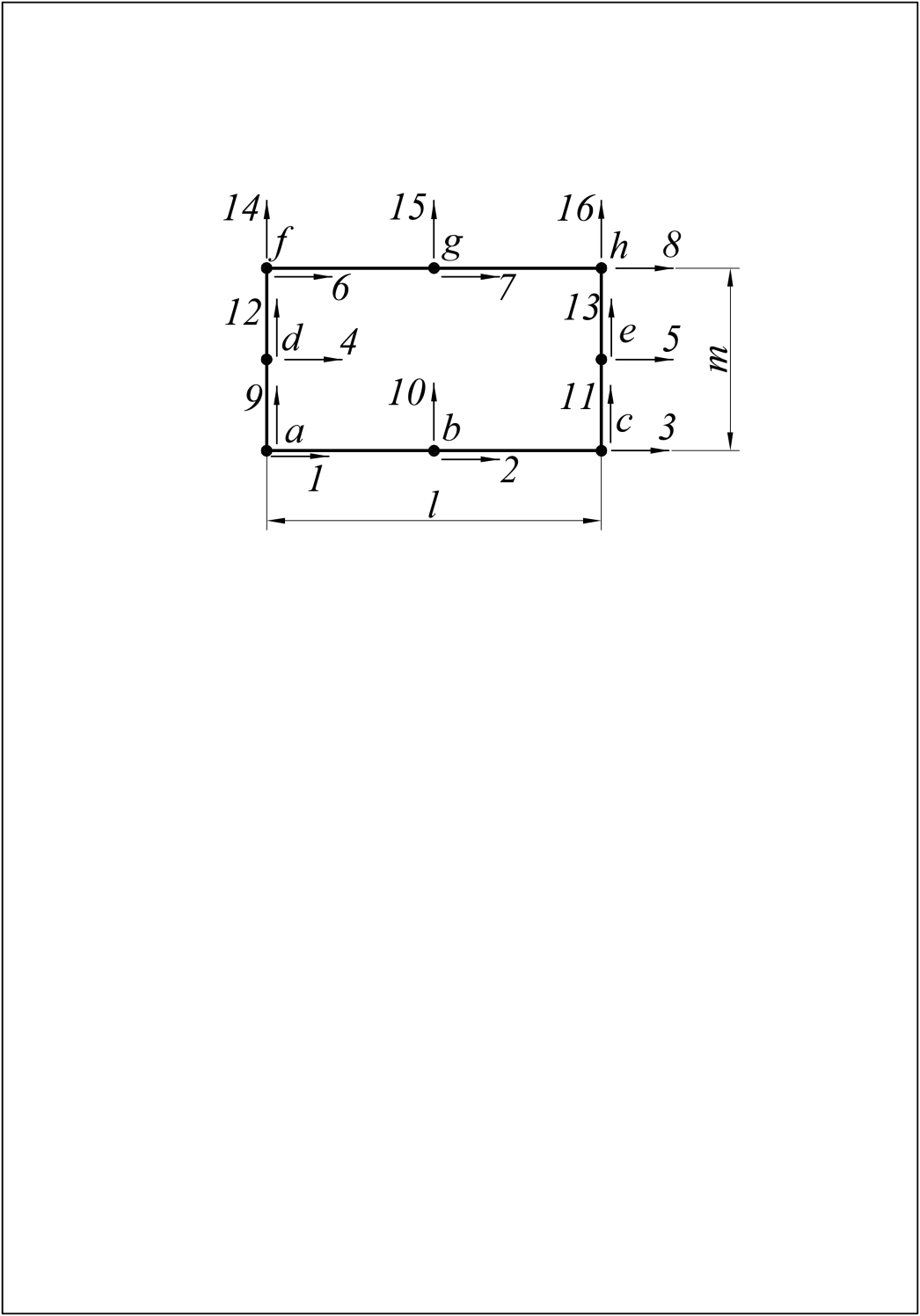
Рис. 29. Восьмиузловой прямоугольник с 16^ю степенями свободы в узлах;