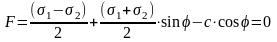- •Нелинейная механика грунтов
- •Дисперсные грунты крупнообломочные грунты
- •Физические характеристики грунтов
- •1.2. Формы расчётных областей, системы координат, правила знаков
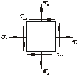
- •1.3. Условия предельного напряженного состояния грунтов
- •Матрицы (1.10), (1.12), (1.13) связаны равенством
- •1.4. Зависимость между перемещениями, напряжениями и деформациями
- •1.5. Расчётные модели геотехнических систем
- •1.5.1. Упрощённые модели
- •Дифференциальные уравнения равновесия. Принцип Лагранжа, равновесие узлов системы мкэ Равновесие тела обрушения и его частей (отсеков). Предельное напряженное состояние в точке
- •Жёстко-пластическая среда
- •Задача Фламана Задача Буссинеска
- •Начальная критическая нагрузка на основание Метод горизонтальных сил г.М. Шахунянца
- •Метод угловых точек
- •1.5.2. Нелинейные модели грунта
- •Контрольные вопросы для самопроверки
- •2. Метод конечных элементов в механике грунтов
- •2.1. Теоретические основы мкэ. Идеи, постулаты
- •2.2. Матрицы жёсткости конечных элементов
- •2.2.1. Общие положения
- •2.2.2. Матрица жёсткости стержневого кэ
- •2.2.3. Функции перемещений континуальных конечных элементов
- •2.2.4. Построение матриц жёсткости континуальных кэ
- •1…16 – Номера степеней свободы
- •2.3. Глобальная матрица жёсткости системы
- •2.3.1. Общая и местная системы координат
- •2.3.2. Формирование систем уравнений
- •2.3.3. О решении системы уравнений
- •2.3.4. Завершающие процедуры статического расчёта
- •2.4. Специальные конечные элементы
- •2.5. Решения физически нелинейных задач средствами мкэ
- •2.6. Заключительные замечания. Ключевые положения мкэ
- •Контрольные вопросы для самопроверки
- •Равновесие узлов системы мкэ. Принцип Лагранжа
- •Уравнение
- •Мора - Кулона
- •Закон Кулона (для заданных поверхностей сдвига)
- •Уравнение Мизеса -
- •Шлейхера - Боткина
- •Закон Гука
- •Смешанная (упругопластическая) задача теорий упругости и пластичности
- •Плоская деформация Пространственная и осесимметричная задача
- •3.2. Программное обеспечение. Критерии предельных состояний
- •3.3. Примеры решения научно-технических задач1
- •Контрольные вопросы для самопроверки
- •Заключительные замечания
- •Библиографический список
- •Сведения из алгебры матриц
- •Понятия, определения
- •Действия с матрицами
- •Давид Моисеевич Шапиро нелинейная механика грунтов
- •3 94006 Воронеж, ул. 20-летия Октября, 84
Равновесие узлов системы мкэ. Принцип Лагранжа
Условия равновесия |
Физические уравнения
|
Геометрические и кинематические соотношения
|
Расчетные модели
|
Уравнение
Мора - Кулона
Закон Кулона (для заданных поверхностей сдвига)
Уравнение Мизеса -
Шлейхера - Боткина
Закон Гука
Соотношения Коши
Кинематические соотношения теории пластического течения
Смешанная (упругопластическая) задача теорий упругости и пластичности


Плоская деформация Пространственная и осесимметричная задача
Рис. 38. Структурная схема упругопластической модели грунта
На рис. 38 представлена структурная схема РМ, сочетающей уравнения теорий линейно деформируемой и жёстко-пластической сред, которые прошли длительный отбор и многократную проверку при проектировании различных категорий сооружений. Получаемое по расчёту напряжённо-деформированное состояние является физически возможным во всех точках. Геометрической иллюстрацией (двухмерной аналогией) упругопластической РМ является диаграмма Прандтля в виде линии 3 на рис. 21.
Постулаты и гипотезы, формирующие принятую модель грунта, и описывающие их уравнения для условий плоской деформации, пространственной и осесимметричной задач представлены в табл. 9.
Для подготовки исходных данных при решении смешанных задач теорий упругости и пластичности требуется шесть параметров каждого слоя грунта: удельный вес γ, модуль деформации Е, коэффициент поперечной деформации ν, угол внутреннего трения φ, удельное сцепление с, параметр дилатансии Λ* или Λ. Для пространственной (осесимметричной) задачи параметры φ и с заменяются другой парой: α≈(sinφ)/3 и k≈ccosφ.
Решение упругопластической задачи. Задача решается средствами МКЭ в сочетании с рассмотренной выше процедурой метода упругих решений по версии «метода начальных напряжений» (МНН).
Введём следующие обозначения: {σ}={σx σy σz τxy τyz τxz σ1 σ2 σ3}, {ε}={εx εy εz γxy γyz γxz ε1 ε2 ε3} – матрицы-строки компонентов напряжений и относительных деформаций в точке (элементарном объёме грунта), конечном элементе или центре конечного элемента. Те же матрицы, содержащие члены с верхним индексом «е» ({σе}, {εе}), означают результаты линейного (упругого) решения задачи. Матрица {σр} содержит компоненты напряжений, удовлетворяющие физическим условиям задачи; при этом одно из условий выполняется на предельном уровне: Fp=0, где Fp – правая часть уравнений, описывающих предельное напряжённое состояние.
Предположим, что на некоторой части расчётной области по результатам линейного расчёта получено распределение напряжений, не удовлетворяющее одному из условий прочности. Его необходимо «исправить», т.е. получить на всей расчётной области физически возможное напряжённое состояние, которое может быть допредельным (Fe<0) или предельным {σр}, определяемым в зависимости от {σе} и соответствующим условию Fp=0.
Учитывая, что грунты слабо сопротивляются растяжению, при котором теряет силу закон сопротивления сдвигу и снижается модуль деформации, будем считать их работающими только на сжатие. Поэтому, если в линейном решении {σе} получено σ1е>0, то принимается σ1р=0. При этом второе главное напряжение должно удовлетворять условиям одноосного сжатия грунтов:
0 ≥σ2е ≥ –2c cosφ/(1–sinφ).
.
Таблица 9
Описание упругопластической модели грунта
Характеристика РМ |
Плоская деформация |
Осесимметричное напряженное состояние |
Учитываемые проявления нелинейности грунта |
1. Пластическое формоизменение при сложном напряженном состоянии |
|
2. Деформирование без сопротивления |
||
3. Сдвиг по заданной (контактной) поверхности |
||
Зависимость между напряжениями и деформациями |
Билинейная в соответствии с диаграммой 3 на рис. 21 |
|
Уравнения закона Гука для линейной части деформации
|
|
|
У 88 равнение предела текучести |
Уравнение Мора-Кулона |
Уравнение Мизеса-Шлейхера-Боткина |
|
|
|
Уравнения для пластических деформаций |
|
|
Дилатансионные соотношения на стадии пластического течения |
|
|
Природное давление в основании, ограниченном горизонтальной плоскостью |
(z1– координата глубины основания, отсчитываемая от его поверхности) |
|

Графической иллюстрацией связей между σ1,2е и σ1,2р являются схемы на плоскости главных напряжений (рисунок 39), где линия ВС изображает уравнение Мора-Кулона Fp=0, точка В – напряжённое состояние σ1=0, σ2=–2ccosφ/(1–sinφ). При σ1е>0, 0 ≥σ2е ≥ –2c cosφ/(1–sinφ) принимается σ1р=0, σ2р=σ2е (точки 1 и 1´). При σ1е>0, σ2е>0 принимается σ1р=0, σ2р=0 (точки 2 и 2´). При σ1е>0,
σ2е<–2c cosφ/(1–sinφ) принимается σ1р=0, σ2р=–2ccosφ/(1–sinφ) (точки 3 и 3´).
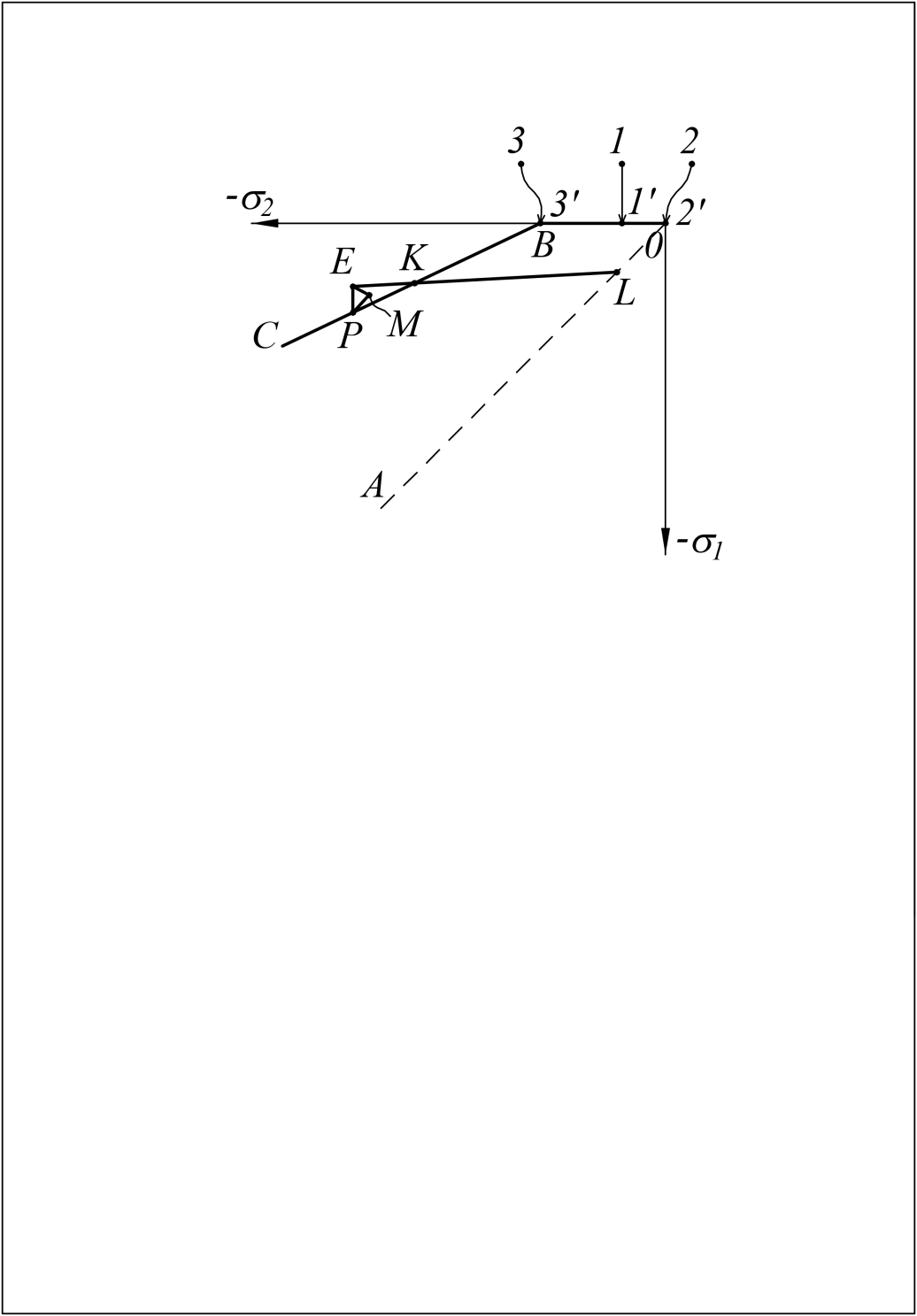
Рис 39. Графическая форма связей между σ1,2р и σ1,2е
на плоскости главных напряжений
При пространственном напряжённом состоянии зависимости, связывающие напряжения σ2е и σ2р, распространяются на σ3е и σ3р.
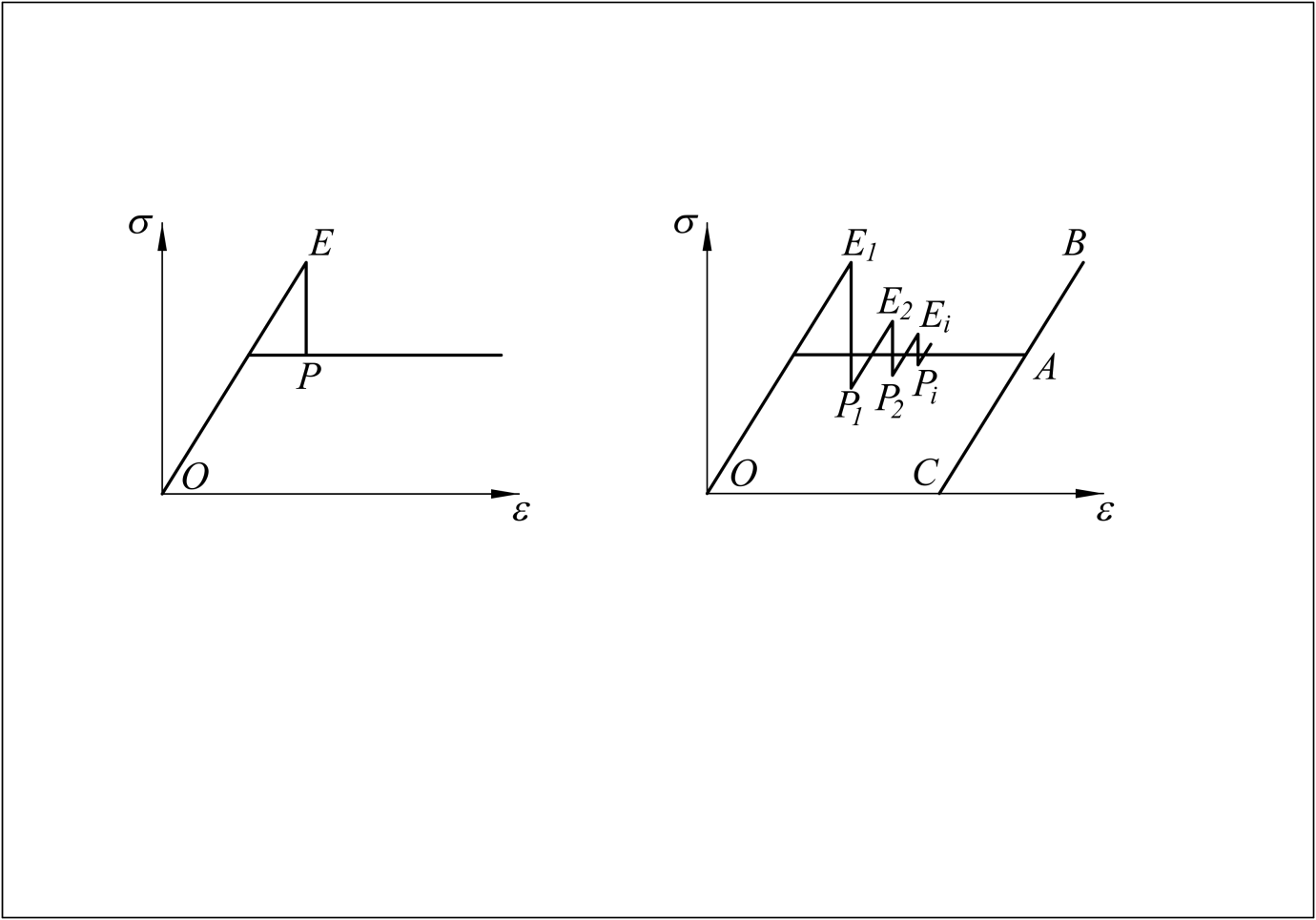
Наибольшее практическое значение имеет случай, когда исходное напряжённое состояние {σе} является всесторонне сжимающим, но не удовлетворяет условию текучести в соответствии с уравнениями Мора-Кулона (1.7) или Мизеса-Шлейхера-Боткина (1.17): Fe>0. Для составления уравнений связи между {σе} и {σр} воспользуемся условием, согласно которому «упругие» деформации {εе}, вызываемые напряжениями {σе}, равны упругопластическим деформациям от напряжений {σр}. Это равенство иллюстрирует рисунок 40, а, где на билинейном графике ε=f(σ) точка Е изображает напряжённо-деформированное состояние {σе}–{εе}, а точка Р – напряжения {σр}, которые требуется определить.
а) |
|
б) |
|
Рис. 40. Графические иллюстрации:
а – к уравнениям (3.1); б – к уравнениям (3.13), (3.14)
Кроме того, в расчёт вводится условие о коаксиальности (соосности) тензоров-девиаторов напряжений и скоростей пластических деформаций, следствием чего является соосность напряжений σ1,2,3е и σ1,2,3р. Это позволяет записать следующие уравнения для условий плоской деформации:
 (3.1)
(3.1)
где
 – модуль сдвига; Е,
ν,
λ,
Λ*
сохраняют значения, принятые в п. 1.4.
Левые части уравнений (3.1) выражают
относительные деформации
– модуль сдвига; Е,
ν,
λ,
Λ*
сохраняют значения, принятые в п. 1.4.
Левые части уравнений (3.1) выражают
относительные деформации
 ,
первые члены правых частей
,
первые члены правых частей
 – «упругие» части главных деформаций
от напряжений {σр},
вторые члены
– «упругие» части главных деформаций
от напряжений {σр},
вторые члены
 – пластическую деформацию формоизменения
c
дилатансией.
– пластическую деформацию формоизменения
c
дилатансией.
Неизвестные главные напряжения должны удовлетворять условию текучести
 .
(3.2)
.
(3.2)
Уравнения (3.1) и (3.2) образуют замкнутую систему, решение которой позволяет получить следующие соотношения связи между σ1,2р и σ1,2е:
 ;
(3.3)
;
(3.3)
 ,
(3.4)
,
(3.4)
где
 .
(3.5)
.
(3.5)
В конечных элементах пластической области Fе>0.
Вернёмся к рис. 39, где на плоскости главных напряжений пограничная прямая линия ВKРС изображает уравнение Мора-Кулона Fp=0, пунктирная линия ОА – гидростатическую ось. Рассмотрим связь между напряжениями σ1,2p и σ1,2е в графической форме. Допустим, что отрезок LE изображает изменение напряжённого состояния в элементарном объёме грунтового массива после приложения нагрузки: точка L (σ1,2=–р) соответствует начальному (природному) давлению; точка Е (σ1,2е) – результат линейного решения задачи, изображаемое ею напряжённое состояние физически невозможно.
В действительности в момент пересечения вектором LE пограничной прямой ВС (точка K) напряжённое состояние переходит в упругопластическую стадию, определяемую ломаной линией ВKР. Точка Р изображает напряжения σ1,2p в соответствии с (3.4). Отрезок ЕР изображает разность между напряжениями σ1,2р и σ1,2е: ЕР=∓Fе(1–2ν±Λ*)/(1–2ν+Λ*sinφ), состоящую из девиаторной ЕМ и гидростатической МР частей:
ЕМ=∓Fе(1–2ν)/(1–2ν+Λ*sinφ), МР=–FеΛ*/(1–2ν+Λ*sinφ).
Для трёхмерной задачи при допущении о соосности σ1,2,3е, ε1,2,3е, σ1,2,3р уравнения, выражающие совместность деформаций и условие прочности, записываются в следующем виде:
 ,
(3.6)
,
(3.6)
 ,
(3.7)
,
(3.7)
где l, m, n – 1, 2, 3, остальные обозначения прежние (см. п. 1.3, 1.4).
Совместное решение этих уравнений относительно σ1,2,3р и λ позволяет получить следующие соотношения связи между σ1,2,3р и σ1,2,3е и их инвариантами:
 ,
(3.8)
,
(3.8)
 ,
,
 ,
(3.9)
,
(3.9)
 ,
(3.10)
,
(3.10)
где
 .
.
Графическая форма связи напряжённых состояний σ1,2,3р и σ1,2,3е аналогична рассмотренной выше на рис. 39, но изображается в пространстве главных напряжений, где условие (3.10), заменяющее (3.4) для плоской задачи, имеет вид конической поверхности.
Изложенный выше способ определения главных напряжений σ1,2,3р и их положения на плоскости σ1, σ2 (в пространстве σ1, σ2, σ3) главных напряжений необходим, но не достаточен для решения упругопластической задачи. При замене относительных деформаций {εе} равными по величине упругопластическими деформациями {εр}+{εп} неразрывность системы сохраняется, но происходит нарушение равновесия, возникает «невязка сил».
Для корректного перехода от напряжений σ1,2,3е к σ1,2,3р необходимо выполнить следующую двухшаговую процедуру МУР на математической основе МКЭ.
Первый шаг.
1. Определение главных начальных напряжений Δσ1,2,3=σ1,2,3р−σ1,2,3е в конечных элементах, в которых получено Fe>0. Переход от главных напряжений Δσ1,2,3 к осевым «начальным напряжениям» Δσx, Δσy, Δσz, Δτxy, Δτxz, Δτyz. Сложение начальных напряжений {Δσ} с компонентами напряжений {σе} линейного (упругого) решения задачи. На этом шаге расчёта в конечных элементах пластической области получены компоненты напряжений {σр}.
2. Определение вектора «невязки силы» в матричной форме в соответствии с соотношениями, принятыми в МКЭ: {ΔР}=V[B]T{Δσ}, где [B]T− транспонированная матрица соотношений Коши, V – объём конечного элемента; в условиях плоской деформации V=St; S – площадь конечного элемнта, t=1 м (см) – толщина расчётной области.
Второй шаг. Наложение вектора сил {ΔР} с обратным знаком (−{ΔР}) на систему (расчётную область) в целом. Определение компонентов напряжений {σΔР} и относительных деформаций {εΔР} путём расчёта системы на воздействие сил {ΔР}. Получение новых напряжений и относительных деформаций в конечных элементах пластической области:
{σ}={σр}+{σΔР}={σе}+{Δσ}+{σΔР},
{ε}={εе}+{εΔР}={εр}+{εп}+{εΔР} (3.11)
и в конечных элементах, в которых исходное (начальное) напряжённое состояние было допредельным:
{σ}={σе}+{σΔР}, {ε}={εе}+{εΔР}. (3.12)
Уравнения (3.11) и (3.12) не являются окончательными записями решения упругопластической задачи. Распределение напряжений в конце «второго шага» необязательно удовлетворяет установленным требованиям. После проверки на выполнение условий прочности на части расчётной области могут остаться или вновь появиться конечные элементы, в которых получено Fе>0. В этом случае новое распределение напряжений и деформаций принимается в качестве исходного, повторяется процедура метода начальных напряжений, а затем, если понадобится, повторяется необходимое число раз. Это означает, что процесс решения упругопластической задачи является итерационным. Итерация заканчивается после того, как величина «начальных напряжений» (или некоторый характеризующий её параметр) удовлетворяет установленному критерию сходимости.
Число ступеней итерации можно уменьшить, а их размер – увеличить, при помощи коэффициента «ускорения сходимости» k>1,0 к величинам {Δσ}={σр}−{σе} в конечных элементах пластической области.
В связи с итерационным путём решения упругопластической задачи требуется корректировка уравнений (3.11) и (3.12) и придание им следующего окончательного вида:
{σе}i+1={σе}i + k ({σp}i−{σе}i)+{σΔР}i, {εe}i+1={εp}i={εe}i+{εΔР}i, (3.13)
{σе}i+1={σе}i+{σΔР}i, {εe}i+1={εp}i={εе}i+{εΔР}i, (3.14)
где i, i+1 − номера ступеней итерации.
Уравнения (3.13) и (3.14) предопределяют алгоритм решения упругопластической задачи, который состоит из следующих расчётов, выполняемых на каждой ступени итерации.
1. Определение исходных компонентов напряжений {σе}i и деформаций {εе}i, полученных после действий предыдущей ступени итерации по уравнениям (3.13) и (3.14).
2. Определение компонентов напряжений {σp}i в соответствии с изложенным выше в настоящем параграфе (уравнения (3.4), (3.11), рис. 39).
3. Выполнение двухшаговой процедуры метода начальных напряжений:
– определение начальных напряжений {Δσ}i={σр}i−{σе}i и вектора «невязки сил» {ΔР}i= kV [B]T{Δσ}i или {ΔР}i= k St[B]T{Δσ}i;
– определение компонентов напряжений {σΔР}i и деформаций {εΔР}i путём расчёта системы на воздействие сил {−ΔР}i.
4. Определение новых компонентов напряжений {σе}i+1 и деформаций {εе}i+1; проверка выполнения условий прочности и сходимости итерации.
Графической иллюстрацией процесса решения с использованием уравнений (3.13) и (3.14) являются ломаные линии на рис. 40, б, где точки Еi изображают напряжённо-деформированное состояние {σе}i−{εе}i в начале i-й ступени итерации на билинейной диаграмме ε=f(σ), а точки Рi – напряжения {σp}i.
При поэтапном приложении нагрузки приращения напряжений {δσе}j j-го этапа загружения добавляются к полученным после (j−1) этапов {σр}i;j-1. Эти суммы принимаются за исходные значения {σе}i=1;j, после чего выполняются расчёты метода начальных напряжений с использованием уравнений (3.13) и (3.14). Такой путь решения графически изображён на рис. 40, б. Пусть точка А обозначает достигнутый уровень напряжений и деформаций после (j−1)-го этапа приложения нагрузки. Отрезок АВ изображает связь напряжений {δσе}j и деформаций {δεе}j в соответствии с линейным решением при j-м догружении. В этом случае использование соотношений (3.13), (3.14) равносильно предположению о том, что начальное напряжённо-деформированное состояние {σе}i=1;j−{εе}i=1;j в точке В состоит из упругой части СВ и ранее накопленных пластических деформаций ОС.
Пример расчёта. Рассмотрим реализацию изложенного выше решения на численном примере задачи о полосовой нагрузке на основании, ограниченном горизонтальной плоскостью.
Однородное основание, разделённое на конечные элементы в виде прямоугольников (рис. 41), загружено полосовой нагрузкой с интенсивностью р=300 кПа и шириной полосы b=6 м в условиях плоской деформации. Для грунта основания приняты следующие характеристики: Е=30 МПа, ν=0,42, φ=200, с=30 кПа, Λ*=0, γ=18 кН/м3.

Рис. 41. Результаты расчета основания полосовой нагрузки
1 – граница пластической области; 2 – конечные элементы зоны разрушения по линейному решению задачи; 3 – направления главных напряжений; 4 – плоскость симметрии
На рисунке 40 заштрихована «зона разрушения» [Fe=½(σ1е − σ2е) + ½(σ1е+ +σ2е)sin φ − c cos φ >0], полученная в результате первого упругого решения. Глубина её проникновения в основание составила 3.6 м. После пяти ступеней итерации величина параметра Fe во всех конечных элементах не превышала 1 кПа, и расчёт был прекращён. При этом пластическая подобласть достигла размеров, очерченных на рисунке.
Перед началом итерации вертикальные перемещения верхней границы основания составляли 5,2 мм в точке Е и 30,6 мм в точке D, горизонтальное перемещение в точке Е – 0,83 мм. В ходе расчёта вертикальные перемещения практически не изменились, а горизонтальное перемещение в точке Е увеличилось на 0,42 мм.
На рис. 42, а изображены круги Мора, соответствующие напряжённому состоянию в центрах конечных элементов № 95 и 75 (см. рис. 41) в начале расчёта (первое упругое решение) и после окончания итерации. На рис. 42, б показана динамика изменения касательных напряжений τmax=½(σ1−σ2) (радиуса круга Мора) в этих же точках на диаграмме γmax=f(τmax). Вертикальные отрезки соответствуют уменьшению касательных напряжений на первом шаге каждой (i-й) ступени итерации, наклонные – приложению системы сил {ΔР}i на втором шаге. Сплошные горизонтальные линии обозначают пластические составляющие деформации в начале расчёта, пунктирные – в конце расчёта. Их несовпадение связано с изменением в ходе итерации среднего нормального напряжения.
а) |
|
б) |
|
Рис. 42. Диаграммы, описывающие итерационный процесс в конечных элементах (КЭ) №75 и №95: а – круги Мора по результатам линейного расчета (1) и в конце итерации (2); б – графики зависимости γmax=½(ε1−ε2)= f(τmax)
Компьютерная реализация этого решения осуществлена в программах START (Д.М. Шапиро, Г.В. Полторак, 1989) для ЭВМ поколения ЕС и УПРОС (2000–2010) для современных РС. В обеих программах реализованы плоская и осесимметричная версии изложенного выше решения упругопластической задачи. Кроме того, на основе того же алгоритма в Полтавском нацональном техническом университете им. Ю. Кондратюка была разработана программа «Основание» (О.А. Голов, 2002), содержащая только плоскую версию.
Программа УПРОС («Упругопластический расчёт объектов строительства») разработана и внедрена автором совместно с кандидатами технических наук Р.Н. Гузеевым и Н.Н. Мельничуком в 2000–2010 г.г. для целей научных исследований и проектирования геотехнических объектов. Являясь результатом научных работ небольшой группы специалистов, эта программа не оснащена качественными пре- и постпроцессорами, графическими интерфейсами. Она предназначена для ограниченного круга пользователей с исследовательскими целями, а также может быть использована для тестирования современных программ промышленного назначения.
В расчётах учитываются рассмотренные выше проявления нелинейности грунтовой среды: пластическое формоизменение с дилатансией, деформирование без сопротивления при растяжении, сдвиг по заданной контактной поверхности. Программа позволяет рассмотреть напряжённо-деформированное состояние при одновременном или постадийном (ступенчатом) приложении нагрузок. Может быть учтено исходное напряжённое состояние, полученное системой на предыдущих стадиях приложения нагрузок, или гидростатически распределённое природное давление в основании.
Библиотека используемых в программе конечных элементов содержится в табл. 10. Компоненты напряжений {σе}i, {σр}i определяются в центрах конечных элементов, моделирующих грунт, внутренние усилия − на концах стержневых конечных элементов, перемещения − в узлах сетки.
В
качестве показателя сходимости итерации
принята норма невязки силы
 ,
где {ΔРs}i
– вектор невязки силы, определяемый в
соответствии с процедурой МНН, s
– номера
узлов, i
– текущая
ступень итерации. Допустимая величина
ЕΔР
задаётся
как часть (3÷5%) аналогичной нормы
,
где {ΔРs}i
– вектор невязки силы, определяемый в
соответствии с процедурой МНН, s
– номера
узлов, i
– текущая
ступень итерации. Допустимая величина
ЕΔР
задаётся
как часть (3÷5%) аналогичной нормы
 действующей
нагрузки {Рs}.
действующей
нагрузки {Рs}.
Итерационный процесс прекращается после снижения нормы «невязки силы» до установленного уровня или исчерпания лимита ступеней итерации.
Вводимая информация состоит из следующих массивов исходных данных:
– координаты узлов;
– связи (узлы с нулевыми перемещениями и узлы с равными перемещениями);
– описание нагрузок (величины, направления, узлы приложения);
– описание конечных элементов (номера узлов, модули деформации, коэффициенты поперечной деформации конечных элементов, моделирующих грунт и массивные конструкции; площади сечения и моменты инерции стержней; механические характеристики грунтов: угол внутреннего трения, удельное сцепление, параметр дилатансии; природное или исходное напряжённое состояние);
– коэффициент ускорения сходимости k;
– допустимая величина нормы невязки силы (параметр ЕΔР);
– максимальное число циклов итерации, после достижения которого расчёт прекращается с выводом об отсутствии сходимости.
Таблица 10
Библиотека конечных элементов, используемых в программе УПРОС
Наименование КЭ |
Форма (схема) КЭ, система координат, векторы степеней свободы |
Компоненты напряжений в континуальных КЭ |
Функции перемещений континуальных КЭ |
Стержень |
|
|
|
Трехузловой треугольный КЭ плоской системы |
|
|
|
Четырехузловой прямоугольный КЭ плоской системы |
|
|
|
Осесимметричный КЭ треугольного сечения |
|
|
|
Выходная информация – результаты расчёта в конце итерации и на указанных в задании ступенях итерации:
– перемещения узлов;
– компоненты напряжений в центрах континуальных конечных элементов;
– продольные, поперечные силы и моменты на концах стержневых элементов;
– данные о наличии и видах пластических явлений в конечных элементах;
– нормы нагрузки ЕР и невязки силы ЕΔР,i.