2.2. Матрицы жёсткости конечных элементов

2.2.1. Общие положения

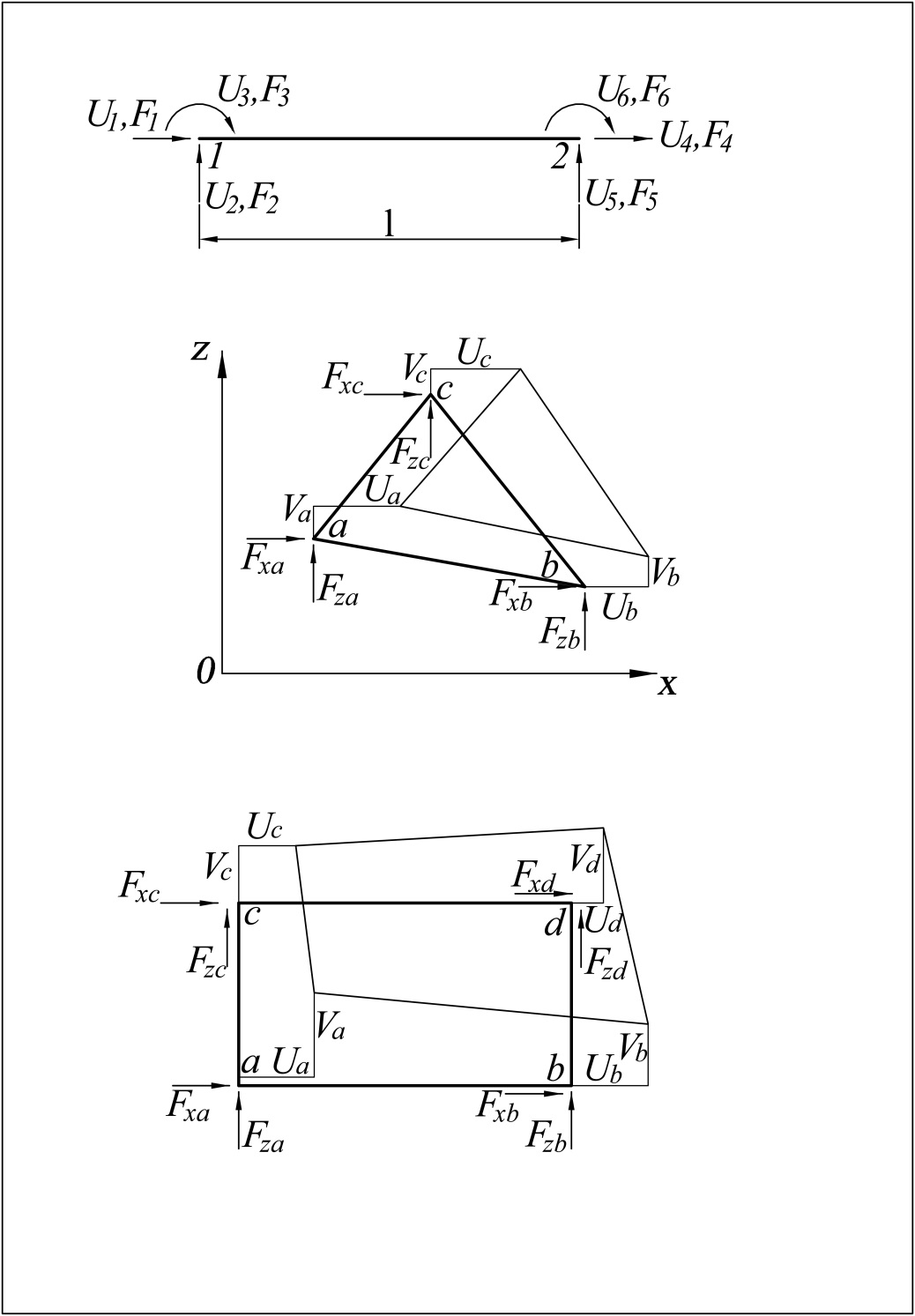
Рассмотрим построение матриц жёсткости КЭ, не касаясь пока вопроса о том, как они используются для решения задач МКЭ. Покажем это на примерах (рисунок 27,а,б,в) стержня общего вида с тремя степенями свободы (связями) на концах, треугольного и прямоугольного КЭ плоской (плоское напряжённое состояние или плоская деформация) системы с двумя степенями свободы в каждой вершине.

а)
б)		в)

Рис. 27. Плоские конечные элементы (а – стержень общего вида, б – треугольник,

в – прямоугольник), перемещения и узловые силы на их концах и вершинах

Предполагается, что действующие силы приложены только в узлах (1, 2 на рисунке 27,а; a, b, с, d на рисунках 27,б,в) и приведены к направлениям перемещений. Матрица жёсткости КЭ содержит коэффициенты уравнений, связывающих векторы сил и перемещений узлов по направлениям координатных осей.

2.2.2. Матрица жёсткости стержневого кэ

В общем виде связь между перемещениями U₁…U₆ и узловыми силами F₁…F₆ (см. рисунок 26,а) с постоянной жёсткостью растяжении-сжатии ЕА и изгибе EI выражается матричным соотношением

{F}=[K]{U}, (2.1)

где

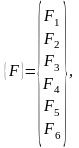
(2.2)

− векторы-столбцы сил и перемещений,

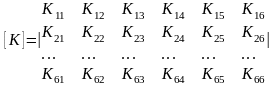(2.3)

− матрица жёсткости КЭ. Каждый коэффициент K_ij выражает реакцию (узловую силу) в закреплении по направлению i-й степени свободы (считая это закрепление неподвижным) на единичное перемещение U _j=1.

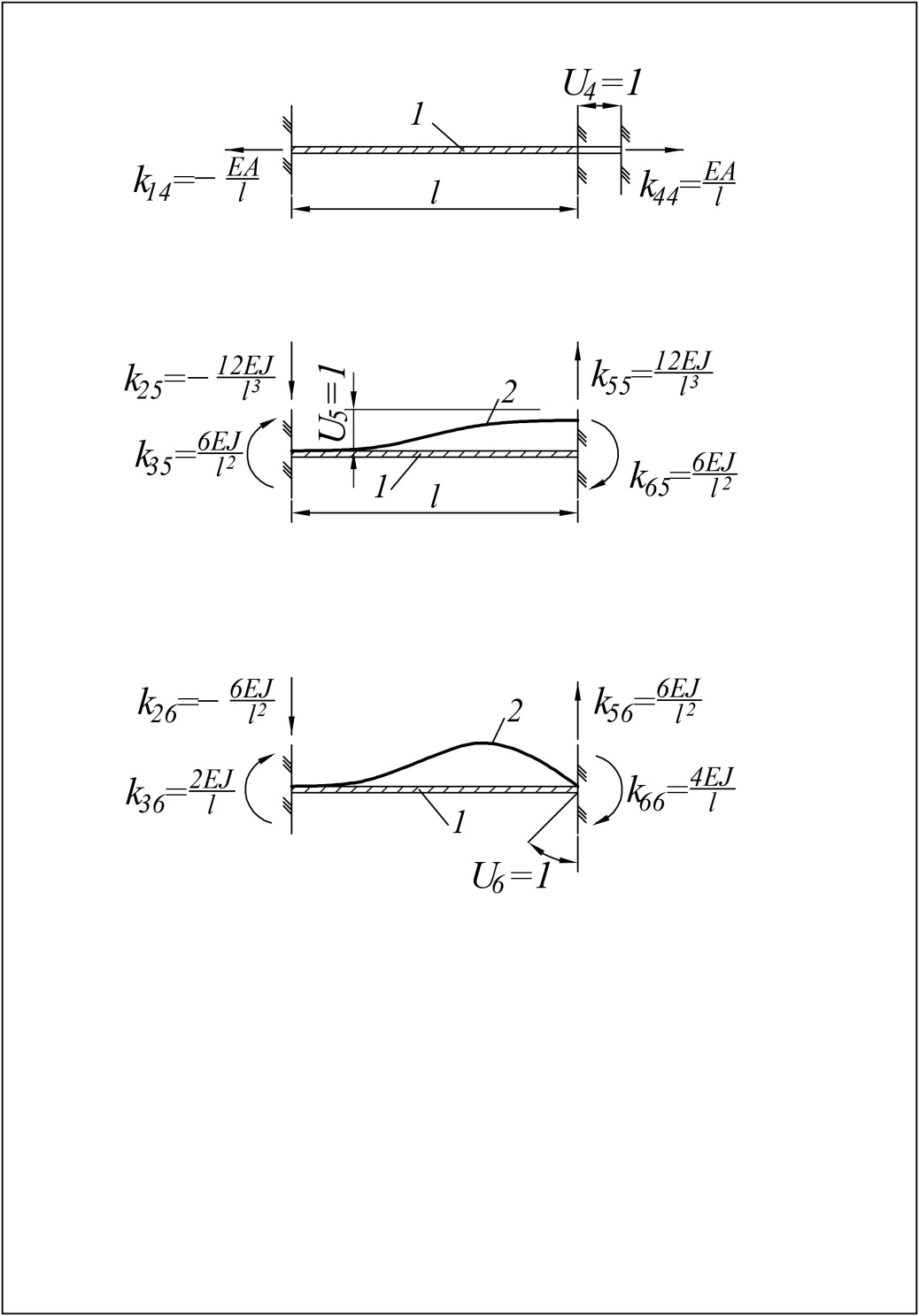
На рисунке 28 показаны возможные перемещения U_j=1 (j=1…6) и вызываемые ими силы K_ij в закреплениях на концах стержня. Так, например, при U₁=1 (рисунок 28,а) K₁₁=EA/l, K₂₁=0, K₃₁=0, K₄₁=−EA/l, K₅₁=0, K₆₁=0. При U₃=1 (рисунок 28,в) K₁₃=0, K₂₃=−6EI/l², K₃₃=4EI/l, K₄₃=0, K₅₃=6EI/l², K₆₃=2EI/l.

а)		б)
в)		г)
д)		е)

Рис. 28. К построению матрицы жесткости стержня общего вида с шестью закреплениями на концах; а…е – усилия в закреплениях при перемещениях U₁… U₆; 1 – первоначальное положение стержня; 2 – деформированная ось; 3 – эпюра моментов

Полная запись системы уравнений (2.1), включающей матрицу жёсткости КЭ, имеет вид:

(2.4)

Аналогичным путём осуществляется построение матриц жёсткости стержневых элементов с другими условиями закрепления концов.

2.2.3. Функции перемещений континуальных конечных элементов

Перейдём к рассмотрению матриц жёсткости плоских континуальных КЭ на рис. 27, б, в, в которых коэффициенты K_ij по-прежнему обозначают реакции в закреплениях при единичных перемещениях узлов. Для того, чтобы выразить коэффициенты K_ij через геометрические и физические характеристики конечных элементов, вводится допущение о форме уравнений (аппроксимирующих функций) для компонентов перемещений.

Выбор аппроксимирующих функций обусловливают следующие требования, которые станут понятными из последующего изложения:

1) количество коэффициентов в степенных полиномах, описывающих компоненты перемещений, должно быть равно числу степеней свободы (определяемых перемещений узлов) КЭ;

2) неразрывность перемещений не только в узлах, но и на границах КЭ; для этого показатели степеней членов полиномов должны быть на единицу меньше числа узлов, скрепляющих контактирующие КЭ.

Здесь используется математическое правило о том, что через п точек можно провести одну кривую, изображающую полином (п–1) порядка, а через две точки – одну прямую.

Покажем построение функций перемещений на примерах простейших КЭ (трёхузлового треугольника и четырёхузлового прямоугольника) континуальных систем.

Треугольный КЭ. Для треугольного КЭ с шестью степенями свободы (см. рис. 27, б) вид функции перемещений представляет собой следующие записи:

u=α₁+α₂x+α₃z, v=α₄+α₅x+α₆z, (2.5)

где u=u(x,z), v=v(x,z) – перемещения в произвольной точке с координатами x и z; α₁…α₆ – неизвестные пока коэффициенты, способ определения которых излагается ниже.

Введём обозначения (см. рис. 27, б): U_a, U_b, U_c, V_a, V_b, V_c – перемещения узлов треугольного КЭ по направлениям координатных осей X, Z; x_a, x_b, x_c, z_a, z_b, z_c – координаты узлов a, b, c. Уравнения (2.5) становятся определёнными, если коэффициенты α_k (k=1…6) выражены через перемещения и координаты узлов a, b, c, которые используются в качестве граничных условий.

Поскольку записи (2.5) распространяются на вершины треугольника, можно записать:

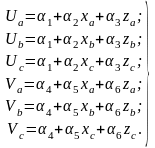. (2.6)

В матричной форме уравнения (2.6) имеют вид:

. (2.6*)

Помещая начало координат в узел а и принимая x_а=0, z_а=0, находим решение системы уравнения (2.6):

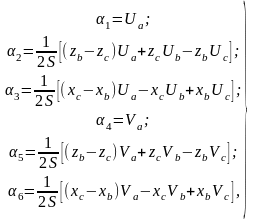(2.7)

где S=½[(x_a–x_b)(z_a–z_c)−(x_a–x_c)(z_a–z_b)]=½(x_bz_c−x_cz_b) – площадь треугольника.

В треугольных КЭ сплошность контакта на границах обеспечена в связи с линейным распределением перемещений. Поскольку смежные КЭ скреплены в двух узлах, то и смежные грани, проходящие через эти узлы, после деформирования остаются на одной (общей) прямой.

Прямоугольный КЭ. Для четырёхузлового прямоугольного КЭ с восьмью степенями свободы (см. рис. 27, в) функции перемещений записываются в следующем виде:

u=α₁+α₂x+α₃z+α₄xz, v=α₅+α₆x+α₇z+α₈xz, (2.8)

где обозначения u=u(x,z), v=v(x,z), x, z, а также α_k, сохраняют те же значения, что в уравнениях (2.5).

Повторим изложенный выше способ определения коэффициентов α_k для прямоугольного КЭ на рис. 26, в, принимая координатные функции в виде уравнений (2.8).

Отметим, что и в этом случае соблюдается равенство числа неизвестных коэффициентов α_k (k=1…8) и степеней свободы узлов. Перемещения на границах распределены линейно, т. е. требование их совместности (непрерывности) выполняется.

Матричная форма уравнений для перемещений узлов имеет следующий вид:

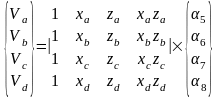, .(2.8*)

Системы уравнений (2.8) так же, как (2.6), разрешимы относительно α_k. Для прямоугольного КЭ с началом координат в узле а решение имеет следующий вид:

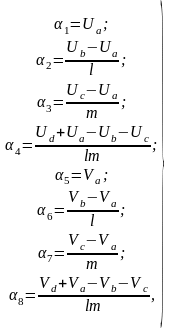(2.9)

где l и m – стороны прямоугольника на рис. 27,в.

* *

*

В табл. 8 представлены формы и функции перемещений наиболее известных плоских и пространственных КЭ, используемых в расчётах конструкций и оснований. Минимальное число узлов (возможные перемещения которых являются степенями свободы) соответствует числу вершин геометрических фигур. Такие КЭ занимают первые пять строк таблицы. Количество неизвестных коэффициентов α_k равно удвоенному (в плоских и осесимметричном КЭ) и утроенному (в пространственных КЭ) числу вершин. Функции перемещений являются полиномами первых степеней координат.

Последние две строки занимают примеры КЭ с удвоенным (по сравнению с минимальным) числом узлов. Функции перемещений в таких КЭ построены на основе многочленов второй степени каждой из переменных. Возможно дальнейшее повышение степени многочленов и увеличение числа узлов (степеней свободы) КЭ. Усложнение КЭ (увеличение числа степеней свободы в одном узле) позволяет повысить точность решения, т. е. эквивалентно увеличению частоты членения расчётной области.

Таблица 8

Характеристика некоторых континуальных КЭ

Наименование КЭ	Форма КЭ, система координат, векторы степеней свободы в узлах	Компоненты напряжений в точках	Функции перемещений
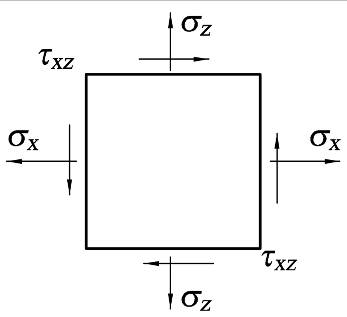
Трехузловой треугольный КЭ плоской системы			u=α1+α2x+α3z v=α4+α5x+α6z
Ч 61 етырехузловой прямоугольный КЭ плоской системы			u=α1+α2x+α3z+α4xz v=α5+α6x+α7z+α8xz
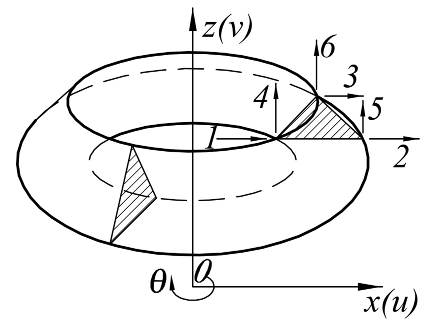
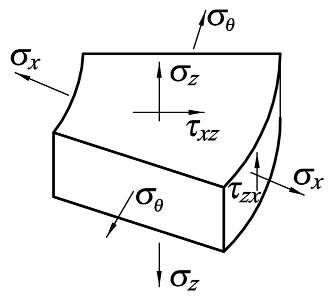
Осесимметричный пространственный КЭ треугольного сечения			u=α1+α2x+α3z v=α4+α5x+α6z

Продолжение табл. 8

Наименование КЭ	Форма КЭ, система координат, векторы степеней свободы в узлах	Компоненты напряжений в точках	Функции перемещений
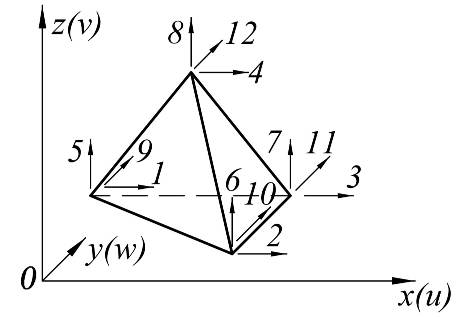
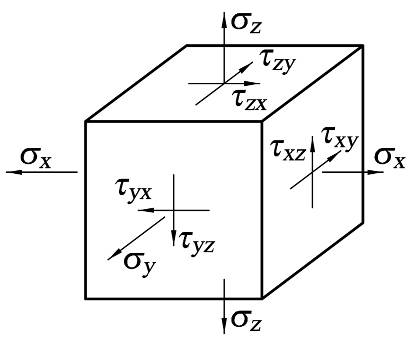
Тетраэдр, пространственное напряженное состояния			u=α1+α2x+α3y+α4z v=α5+α6x+α7y+α8z w=α9+α10x+α11y+α12z
П 62 араллелепипед, пространственное напряженное состояние			u=α1+α2x+α3y+α4z+ +α5xy+α6yz+α7xz+α8xyz v=α9+α10x+… w=α17+α18x+…

Окончание табл. 8

Наименование КЭ	Форма КЭ, система координат, векторы степеней свободы в узлах	Компоненты напряжений в точках	Функции перемещений
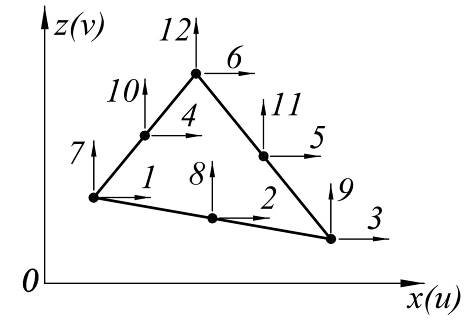
Шестиузловой треугольный КЭ			u=α1+α2x+α3z+α4xz+ +α5x2+α6z2 v=α7+α8x+α9z+α10xz+ +α11x2+α12z2
В 63 осьмиузловой прямоугольный КЭ			u=α1+α2x+α3z+α4xz+ +α5x2+α6z2+α7x2z+α8xz2 v=α9+α10x+α11z+α12xz+ +α13x2+α14z2+α15x2z+α16xz2