Матрицы (1.10), (1.12), (1.13) связаны равенством

. (1.14)

Шаровой тензор вызывает изменение объёма, девиатор – формоизменение.

2. Использование инвариантов напряжённого состояния, т. е. таких комбинаций напряжений, которые не меняют своих значений при повороте осей. Наибольшее практическое значение имеют первый инвариант тензора напряжений

(1.15)

и второй инвариант девиатора напряжений

. (1.16)

Ось симметрии ОА на рис. 12, а изображает гидростатические напряжённые состояния . Эта прямая наклонена к осям под равными углами и является нормалью к девиаторной плоскости, проходящей через начало координат и определяемой тем, что суммы координат её точек .

Покажем способ получения инвариантов I1, I2 и доказательство их независимости от положения осей координат. Выполним для этого следующие построения. В параллелепипеде на рисунке 13 выделим тетраэдр, образованный наклонной плоскостью, пересекающей оси координат Х, Y, Z. Предположим, что выбранная (обозначенная штриховкой) наклонная плоскость является одной из трёх главных площадок в рассматриваемой точке, и нормаль v параллельна σ – одному из трёх главных напряжений. Рис. 13. Схема к уравнениям (1.13) Обозначим через l, m, n направляющие косинусы нормали v по отношению к осям Х, Y, Z. Направляющие косинусы связаны соотношением l2+m2+n2=1. (a) Отношения площадей граней, лежащих на координатных плоскостях, к площади Fv главной площадки, нормальной к оси v, будут равны Fyz/Fv=l, Fxz/Fv=m, Fxy/Fv=n. Запишем три уравнения равновесия проекций напряжений на оси Х, Y, Z: Fv [(σx–σ)l+τxym+τxzn]=0; Fv [τyxl+(σy–σ)m+τyzn]=0; (б) Fv [τzxl+τzym+(σz–σ)n]=0 и ли (σx–σ)l+τxym+τxzn=0; τyxl+(σy–σ)m+τyzn=0; (1.17) τzxl+τzym+(σz–σ)n=0. В высшей алгебре системы уравнений этого вида называются однородными с двумя вариантами решения относительно неизвестных, которыми в нашем случае являются направляющие косинусы l, m, n. Первый вариант – l, m, n равны нулю. Это невозможно, так как противоречит уравнению (a). Второй вариант – определитель системы (1.17) равен нулю: (в) Раскрытие определителя (в) ведёт к кубическому уравнению следующего вида: σ3 – I1σ2 – I2σ – I3=0. (1.18) Три корня уравнения (1.18) являются значениями трёх главных напряжений σ1, σ2, σ3. Коэффициенты уравнения (1.18) являются инвариантами тензора напряжений: I 1=σx+σy+σz, I2=–σx σy – σy σz – σzσx + τxy2 + τyz2 + τzx2, (1.19) I3=σxσyσx – σx τyz2 – σy τxz2– σz τxy2+2τxy τyz τxz. Инвариантность выражений (1.19) обосновывается тем, что при одних и тех же значениях главных напряжений σ1, σ2, σ3 коэффициенты I1, I2, I3 не зависят от положения координатных осей. Решение системы (1.17) можно получить путём подстановки вместо σ одного из трёх главных напряжений, полученных в результате решения кубического уравнения (1.18), совместно с уравнением (а). Получим теперь инвариант I2 для условий девиатора напряжений в соответствии с (1.13). Для этого в запись этого инварианта в составе (1.19) вместо σx,y,z введём выражения (σx,y,z–⅓I1), а последние три члена τxy2+τyz2+τzx2 оставим без изменения и временно исключим из рассмотрения. Выполним тождественные преобразования с первыми тремя членами: –(σx–⅓I1)(σy–⅓I1) –(σy–⅓I1)(σz–⅓I1)–(σz–⅓I1)(σx–⅓I1)= =–[σxσy–⅓I1(σx+σy)+(⅓I1)2]–[σyσz–⅓I1(σy+σz)+(⅓I1)2]– –[σzσx–I1(σz+σx)+(⅓I1)2]= =–σx σy – σy σz – σzσx+⅔I12–⅓I12=–σx σy – σy σz – σzσx+⅓I12= =–σx σy – σy σz – σzσx+⅓(σx2+σy2+σx2+2σx σy+2σy σz+2σzσx)= =⅓(σx2+σy2+σx2–σx σy – σy σz – σzσx)= [(σx–σy)2+(σx–σy)2+(σx–σy)2]. Присоединяя к последнему выражению τxy2+τyz2+τzx2, получаем окончательный вид второго инварианта девиатора напряжений в соответствии с (1.16): I2= [(σx–σy)2+(σx–σy)2+(σx–σy)2]+τxy2+τyz2+τzx2= = [(σx–σy)2+(σx–σy)2+(σx–σy)2+6τxy2+6τyz2+6τzx2].

В механике грунтов при анализе пространственного напряжённого состояния используется условие прочности Мизеса-Шлейхера-Боткина, описываемое уравнением

, (1.20)

где и – прочностные характеристики грунта, подобные 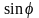и с в уравнении (1.7).

Графической формой уравнения (1.20) является коническая поверхность, ось которой совпадает с гидростатической (рис.12, а). Физически возможными являются напряжённые состояния , изображённые на рис.12, а точками М, находящимися на конической поверхности (1.20) или внутри неё.

Уравнение (1.20) тождественно соотношению с более конкретным физическим содержанием, выражающему предельное равновесие на октаэдрической площадке, аналогичное закону Кулона:

, (1.21)

где , – касательное и нормальное напряжения на октаэдрической (равнонаклонённой с осям главных напряжений, рис.12, в) площадке; ρ_окт и п_окт – прочностные характеристики грунта. Уравнения (1.20) и (1.21) тождественны при и .

Уравнение (1.7) и тем более (1.20), (1.21) изменяют первоначальное представление о механизме разрушения грунта. Если по закону Кулона это явление происходит как взаимное смещение частей сыпучего тела, то условия прочности Мора-Кулона и Мизеса-Шлейхера-Боткина объясняют разрушение как результат формоизменяющего (девиаторного) воздействия приложенных сил.

Испытание грунта методом трёхосного сжатия. Физической иллюстрацией формы разрушения в соответствии уравнениями (1.7) и (1.20) является лабораторное испытание образцов грунта цилиндрической формы в соответствии с ГОСТ 12248-2010 в приборе трёхосного сжатия (стабилометре) с принципиальной схемой на рис. 14. Прибор допускает деформации образца грунта в радиальном направлении при фиксированном (контролируемом) горизонтальном давлении. Размеры образца: диаметр не менее 35 мм, отношение высоты к диаметру от 1,85:1 до 2,25:1.

Опыт заключается в приложении к образцу грунта (ненарушенного сложения с природной влажностью или нарушенного сложения с заданными значениями плотности и влажности) осесимметричной системы сил (рис. 15, а): вертикальных σ₃ и горизонтальных

Рис. 14. Принципиальная схема прибора для испытания грунта методом трехосного сжатия: 1 – основание камеры; 2 – корпус камеры; 3 – вентиль для выпуска воздуха; 4 – шток; 5 – образец грунта в оболочке; 6 – верхний штамп; 7 – нижний штамп; 8 – трубки для дренирования и измерения порового давления; 9 – трубка для заполнения камеры и измерения давления в камере; 10 – манометр; 11 – индикатор; 12 – жидкость

а)	б) Рис. 15. К анализу результатов испытания грунта методом трехосного сжатия: а – схема приложения напряжений σ3 и σ1,2 к образцу грунта; б – определение j и с

(радиальных) напряжений 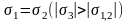. При каждом отдельном испытании радиальные напряжения σ_1,2 остаются постоянными, а напряжения σ₃ увеличиваются небольшими ступенями. Испытание считается законченным после исчерпания прочности грунта по одному из следующих признаков: разрушение образца; пластическое течение без приращения напряжений σ₃; достижение относительной деформацией величины ε₃ = − 0,15. Опыт повторятся не менее трёх раз (с тремя образцами исследуемого грунта) при разных значениях радиальных напряжений σ_1,2. По результатам измерений по известным значениям пар главных напряжений (σ΄_1,2, σ΄₃; σ˝_1.2, σ˝₃; σ˝΄_1.2, σ˝΄₃) определяются значения прочностных характеристик (φ и с или α и k) расчётным путём в соответствии с уравнениями (1.7) или (1.20) или графически при помощи диаграмм на рис. 15,б.

ГОСТ 12248-2010 предусматривает три варианта проведения опыта:

– неконсолидированное-недренированное испытание – для опре-деления сопротивления сдвигу водонасыщенных глинистых, органо-минеральных и органических грунтов природной плотности;

– консолидированное-недренированное испытание с измерением порового давления – для определения характеристик прочности φ и с для водонасыщенных в природных условиях дисперсных грунтов;

– консолидированное-дренированное испытание – для определения характеристик прочности φ, с и характеристик деформируемости Е, ν дисперсных грунтов.