2.4. Специальные конечные элементы

Из числа специальных КЭ наиболее употребительными являются две разновидности: связи конечной жёсткости и жёсткие вставки.

Связи конечной жёсткости. Рассматриваемый вид КЭ (рис. 34,а,б) используется для описания упругоподатливых связей (условных «пружин») в узлах, на внешних границах или на контактах элементов внутри расчётных областей. Связи конечной жёсткости задаются по направлениям осей в глобальной системе координат.

а) б)

Рис. 34. Связи конечной жёсткости: в узле на внешней границе (а)

и на контакте внутри (б) расчётной области; k, l – номера узлов

КЭ в узле на внешней границе описывает связь конечной жёсткости по направлению одной степени свободы. Это может быть сила, вызывающая единичное перемещение узла по направлению одной из осей X, Y, Z, или момент, вызывающий единичный поворот относительно одной из тех же осей.

КЭ, моделирующие упругоподатливые связи внутри расчётных областей, описываются как силы, вызывающие взаимное единичное перемещение узлов по направлениям осей X, Y, Z или взаимный единичный поворот узлов относительно тех же осей.

Описание упругоподатливой связи состоит из кода направления и числа, выражающего жёсткость связи (условной «пружины») при растяжении-сжатии (если связь противодействует продольному перемещению) или при повороте. Размерность задаваемой жёсткости упругоподатливых КЭ – Н или Нм.

Жёсткие вставки. Применение жёстких (бесконечно жёстких) фрагментов расчётных областей МКЭ является полезным (а иногда – незаменимым) инструментом инженерной схематизации.

Жёсткое тело представляется в виде группы узлов, расстояния между которыми остаются неизменными. В такой группе один узел ведущий, остальные –ведомые. Поступательные u_i и угловые θ_i перемещения ведомых узлов связаны с соответствующими перемещениями u₀, θ₀ ведущего узла следующими соотношениями:

θ_i = θ₀, u_i= u₀+θ₀r_0-i, (2.46)

где r_0-i – радиус-вектор, соединяющий ведущий и ведомый (i-й) узлы.

Примером использования процедуры жёсткой вставки может быть расчёт фундамента в виде жёсткого штампа. На расчётной схеме такого фундамента выделяется один ведущий узел с перемещениями u₀, θ₀, а остальные будут ведомыми со связями между перемещениями по соотношениям (2.46).

2.5. Решения физически нелинейных задач средствами мкэ

Решение нелинейных задач МКЭ складывается (и это будет показано в дальнейшем) из процедурной основы (известного из теории математического процесса) и её содержательного наполнения: физических уравнений или соотношений. Физические уравнения (соотношения) отражают конкретные формы пластического деформирования, содержание расчётных моделей. Их рассмотрение вынесено содержится в третьем разделе.

Под процедурной основой понимаются канонические методы, представляющие собой (применительно к МКЭ) решения рекуррентных (повторяющихся) последовательностей систем линейных уравнений. В теории пластичности таких методов существует несколько. Ниже рассматриваются приёмы решения нелинейных задач МКЭ, которые наиболее широко используются в современном программном обеспечении (программы ANSYS, PLAXIS, Midas GTS и др.): метод упругих решений, метод Ньютона–Рафсона. Понятие об обоих методах даётся в виде схематичных описаний и двухмерных аналогий.

Метод упругих решений. Двухмерная аналогия итерационного процесса метода упругих решений (МУР) изображена на рис. 35. Кривая 0–1–2–i–(i+1) изображает нелинейную связь между перемещениями U и внешней нагрузкой F в соответствии с физическими условиями задачи. Примем линейный оператор Е₀=tgθ₀, соответствующий начальному модулю упругости (начальным деформационным параметрам системы). Точка 1^´ на пересечении координат F, U₁ изображает начальное упругое решение задачи. В действительности перемещениям U₁ на части расчётной области соответствует нагрузка F₁ (точка 1). Элементы расчётной области (каждый, где это требуется, в отдельности) разгружаются от напряжений, вызванных силами ΔF₁=F–F₁. Условия задачи выполнены, но образовалась невязка сил ΔF₁. Затем (в соответствии с кусочной диаграммой 1´–1–2´ на рисунке 35) расчётная область (в целом) нагружается этими силами (но противоположного направления), приложенными в тех же точках, сохраняя при этом начальный линейный оператор Е₀.

Рис. 35. Схема итерационного процесса метода упругих решений

В общем виде восходящая ветвь итерационного процесса МУР на одной ступени итерации описывается условным уравнением

Е₀ (U_i+1–U_i)=F–F_i . (2.47)

В научной литературе известно ещё одно название этого метода: метод начальных напряжений (МНН).

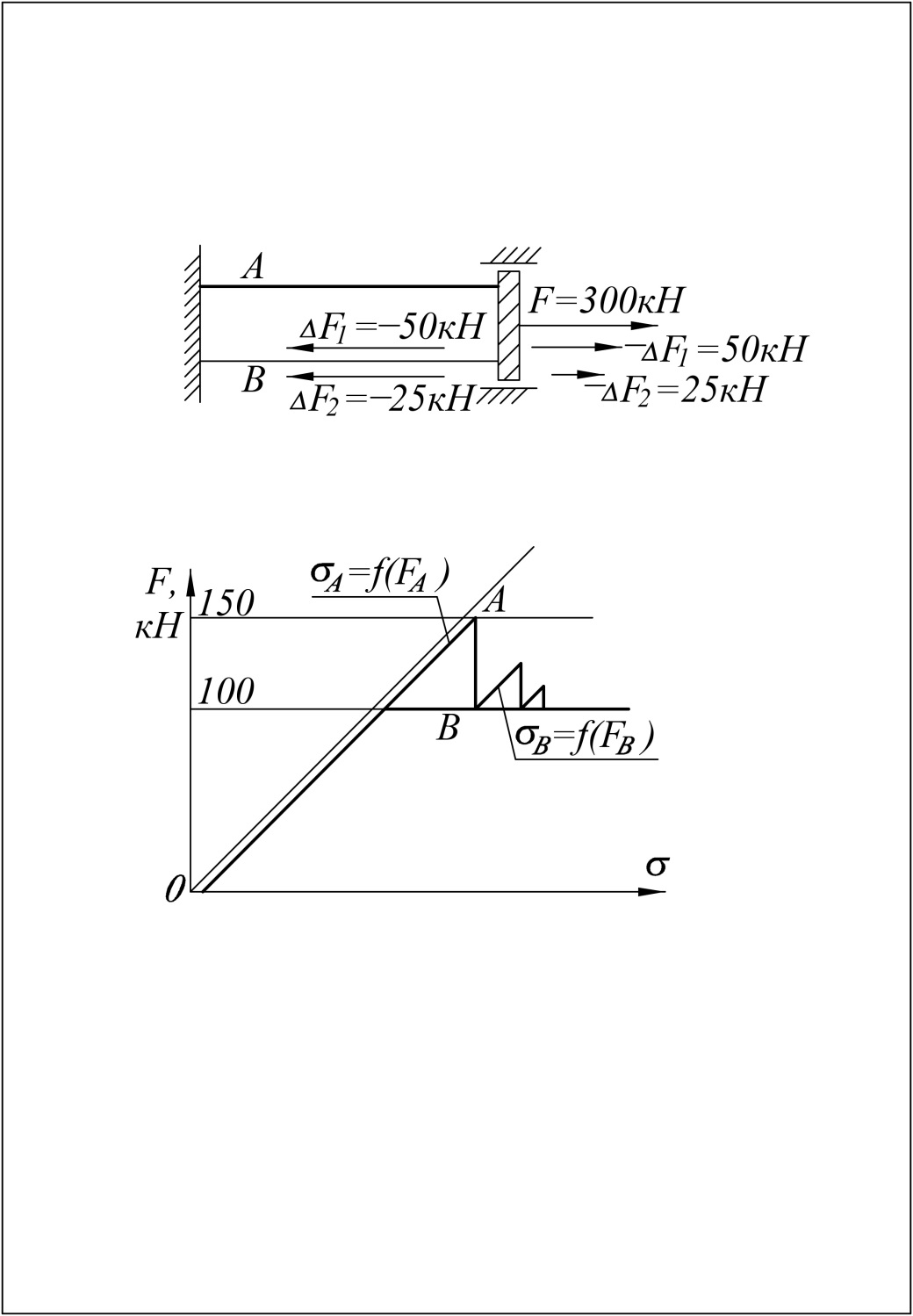
Рассмотрим процедуру МУР-МНН на примере задачи о совместном растяжении силой F=300 кН нитей А и В, объединённых диском С (рис. 36, а). Диск С закреплён от поворота и поперечного смещения и свободно перемещается в направлении силы F. Диаграммы δ=f(F_А,В) растяжения нитей изображены на рис. 35, б. Нить А растягивается упруго без предела текучести; нить В растягивается в соответствии с билинейной диаграммой с пределом текучести 100 кН. Жёсткости обеих нитей (до достижения предела текучести нитью В) равны. Решение задачи очевидно: сила F=300 кН распределяется между нитями на 200 кН (нить А) и 100 кН (нить В).

Получим тот же результат при помощи решения задачи методом упругих решений.

Вначале получим линейное решение: сила F=300 кН распределяется между нитями А и В поровну – F_А=F_В=150 кН. Этот результат противоречит условию задачи о пределе текучести нити В на уровне F_В=100 кН. Приложим к нити В сжимающую силу ΔF=–50 кН. Теперь условия задачи соблюдены, но имеет место невязка силы ΔF₁=–50 кН. Чтобы её компенсировать, увеличим силу F на 50 кН и приложим её в той же точке, что и сила F=300 кН.

а)	б)

Рис 36. Схема (а) и диаграммы u=f(F_А,В) (б)

к задаче о совместном растяжении нитей А и В

Разделим дополнительную силу –ΔF₁=50 кН между нитями А и В в соответствии с решением линейной задачи на равные части по 25 кН. Теперь F_А=150+25=175 кН, F_В=150–50+25=125 кН; часть продольной силы, которую неспособна воспринять нить В, составляет 25 кН. К нити В прикладывается сжимающая сила ΔF=–25 кН. Теперь невязка силы ΔF₂=–25 кН. Чтобы её компенсировать, увеличим силу F на величину –ΔF₂=25 кН. После деления ΔF₂=25кН между двумя нитями на равные части, получим F_А=150+25+12.5=187,5 кН, F_В=150–50+25–25+12,5=112,5 кН.

Процесс можно продолжить. После каждой новой ступени расчёта (итерации) невязка силы уменьшается в два раза: ΔF₃=–12,5 кН, ΔF₄=–6,25 кН и т. д.; силы F_А и F_В становятся ближе к своим конечным значениям 200 и 100 кН.

Рассмотренный пример показывает, что на каждой (i-й) ступени итерационного процесса МУР вычисления выполняются в два шага.

1. Выявляется пластическая подобласть (в рассмотренном примере – нить В), в которой нагрузки (напряжения), полученные на предыдущей ступени расчёта, превышают предел текучести. На пластическую подобласть накладываются силы, переводящие её в физически возможное напряжённое состояние. Определяется невязка силы.

2. Устранение невязки силы: те же силы, но с противоположным знаком, прикладываются ко всей расчётной области.

При расчётах континуальных (плоских, пространственных) систем «невязка сил» {ΔF}_i в узлах КЭ образуется из «невязки напряжений» {Δσ}_i на его континууме на i-й ступени итерации при помощи матричного соотношения

{ΔF}_i=∫[B]^T{Δσ}_idV, (2.48)

где V, [B]^T – объём пространственного КЭ (или произведение площади S на толщину t плоского КЭ) и транспонированная матрица соотношений Коши.

Получаемые при этом векторы {ΔU_i} накапливаются и складываются с начальными перемещениями упругого расчёта. Расчёт доводится до значений {ΔU_i} или {–ΔF_i}, близких к нулю. Параметры {ΔU_i} или {–ΔF_i} удобно использовать в качестве меры невязки.

Главными достоинствами МУР являются ясность физического содержания и постоянство в процессе расчёта начальной «упругой» матрицы жёсткости системы. Это качество иллюстрирует параллельность наклонных отрезков диаграмм на рис. 35 и 36,б.

Недостаток метода – не всегда быстрая сходимость итерации. Наиболее известный способ ускорения сходимости – использование повышающих коэффициентов к невязкам напряжений и сил.

Например, если в рассмотренной выше задаче о растяжении нитей А и В к невязке силы ΔF₁=–50 кН применить повышающий коэффициент 2,0, то получим ΔF₁=–50×2=–100 кН. Повторив те же действия, что и ранее, получим F_А=150+100/2=200 кН, F_В=150–100+100/2=100 кН. Решение с нулевой невязкой получено за одну ступень итерации.

Метод Ньютона–Рафсона (рис. 37) является развитием МУР. Его отличие заключается в определении (в зависимости от достигнутого уровня деформации) и использовании на каждой (i+1)-й ступени итерации переменных деформационных параметров Е_i=tgθ_i.

Лучи 0–1´, 1–i´, изображающие на рис. 37 зависимости между приращениями перемещений ΔU_i+1=U_i+1–U_i и нагрузками F–F_i, являются касательными к кривой 0–1–i–(i+1). Вычислительную схему метода Ньютона–Рафсона характеризует следующее условное уравнение восходящей ветви одной ступени итерации:

Е_i (U_i+1– U_i)=F–F_i . (2.49)

Рис. 37. Схема к математической процедуре метода Ньютона-Рафсона

Метод Ньютона–Рафсона позволяет ускорить сходимость за счёт сокращения числа ступеней итерации, но на каждой ступени необходимо заново строить матрицу жёсткости. При этом в соотношениях [D] связи деформаций и напряжений теряется симметрия, и нулевые члены, отражающие в законе Гука независимость объёмного деформирования от формоизменения, заменяются значащими числами.