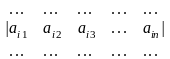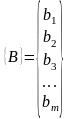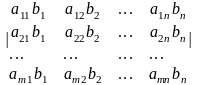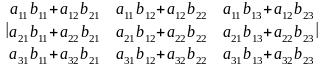Сведения из алгебры матриц

Наименование

понятий

Определение,

содержание понятий

Примеры, обозначения

Матрица

Система чисел,

расположенных

в прямоугольной

таблице

Элемент (член)

матрицы

Число в составе

матрицы

α_ij

Строка матрицы

Горизонтальный ряд чисел в матрице

Столбец

Вертикальный ряд

матрицы

Квадратная матрица

Число членов в строках (сталбцов) n и число строк m равны (m=n)

Прямоугольная матрица

n≠m

Матрица–строка

m=1

{A}={a₁ a₂ a₃ … a_n}

Матрица–столбец

n=1

Размер матрицы

Число членов строк и столбцов матрицы

m ^x n

Наименование действия

Характеристика

(описание) действия

Примеры, обозначения

Сложение (вычитание) матриц

Матрицы–слагаемые должны быть одинакового размера

Складываются

(вычитаются) соответствующие элементы матриц–слагаемых

[C]=[A]±[B]

c_ij=a_ij±b_ij

Умножение матриц на число

Каждый элемент матрицы–произведения [B] равен проиозведению соответствующего

элемента матрицы [A] на число α

[B]=α[A]

b_ij =α a_ij

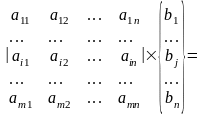
Умножение

прямоугольной матрицы на матрицы–столбец.

Число элементов (размер) строки прямоугольной матрицы равно размеру матрицы–столбца

Каждый элемент

матрицы–произведения получается путем умножения элемента строки α_ij прямоугольной матрицы на

элемент b_j матрицы столбца

[C]=[A]х[B]=

c_ij=a_ij b_j

Наименование действия

Характеристика

(описание) действия

Примеры, обозначения

Умножение

прямоугольных матриц

Строки первой матрицы перемножаются со столбцами второй. Каждый член матрицы–произведения равен сумме произведений элементов строки

первой матрицы (сомножителя) на соответствующие элементы столбцов второй

матрицы (сомножителя) Произведение двух матриц не обладает

переместительным свойством:

[A]х[B]≠ [B] х[A]

Транспонирование матриц

Замена строк столбцами и столбцов строками

[A]^T – транспонированная матрица [A]

Введение.......................................................................................................

3

1. Определяющие уравнения и расчётные модели механики грунтов.............................................................................................................

5

1.1. Классификация и физико-механические характеристики грунтов. Строение оснований..................................................................

5

1.2. Формы расчётных областей, системы координат, правила знаков.......................................................................................................

12

1.3. Условия предельного состояния грунтов.......................................

14

1.4. Зависимость между напряжениями и деформациями ..................

28

1.5. Расчётные модели геотехнических систем....................................

40

1.5.1. Упрощённые модели.............................................................

40

1.5.2. Нелинейные модели грунтов................................................

45

Контрольные вопросы для самопроверки ............................................

48

2. Метод конечных элементов в механике грунтов..................................

50

2.1. Теоретические основы МКЭ. Идеи, постулаты.............................

50

2.2. Матрицы жёсткости конечных элементов.....................................

54

2.2.1. Общие положения..............................................................

54

2.2.2. Матрица жёсткости стержневого КЭ...................................

55

2.2.3. Функции перемещений континуальных КЭ....................

57

2.2.4. Построение матриц жёсткости континуальных КЭ...........

64

2.3. Глобальная система уравнений.......................................................

73

2.3.1. Общая и местная система координат...................................

73

2.3.2. Формирование уравнений глобальных систем...................

74

2.3.3. О решении системы уравнений............................................

77

2.2.4. Завершающие процедуры статического расчёта............

78

2.4. Специальные конечные элементы..............................................

79

2.5. Решение физически нелинейных задач средствами МКЭ..........

80

2.6. Заключительные замечания. Ключевые положения МКЭ........

84

Контрольные вопросы для самопроверки............................................

85

3. Смешанная (упругопластическая) задача теорий упругости и пластичности грунтов. Нелинейный расчёт геотехнических объектов...

86

3.1. Упругопластическая задача для грунтов....................................

86

3.2. Программное обеспечение. Критерии предельных состояний.................................................................................................

98

3.3. Примеры решения научно-технических задач...............................

103

Контрольные вопросы для самопроверки............................................

113

Заключительные замечания........................................................................

114

Библиографический список....................................................................

116

Приложение. Сведения из алгебры матриц..........................................

118