Учебное пособие 800628

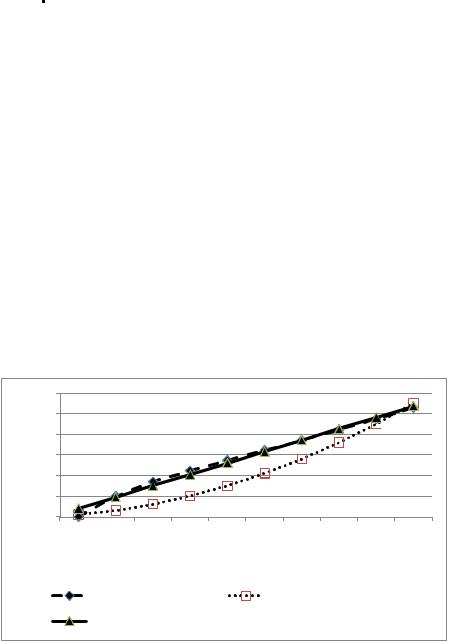
и диагонального вида относительно побочной диагонали, то есть соответствовать представленной в табл. 1.

В указанной выше работе [5] доказано, что именно для матрицы, указанной в табл. 1. оценки латентных переменных будут абсолютно линейными пропорционально номерам оцениваемых объектов и индикаторных переменных, которые участвуют в оценивании.

Таблица 1 Матрица индикаторных переменных для проверки линейности модели при 10

индикаторных переменных и 10 объектов

Решаем задачу оценивания латентных показателей для объектов с данными uij, указанными в табл. 1 аддитивным методом (1), классическим методом Раша, основанном на МП и методом Раша, основанном на МНК. Далее, нормируем полученные оценки на единую шкалу для сравнения результатов оценивания. Оценки по МП методу Раша осуществляется с помощью специализированного программного обеспечения RUMM 2020, по МНК методу Раша - в MS Excel, с помощью надстройки «Поиск решений».

В результате проведенного оценивания и нормирования результатов на единую шкалу, получим результаты, представленные на рис. 1 и рис. 2.

Рис. 1. Значения оценок объектов, полученные аддитивным методам, а также методом Раша, основанным на МП-методе и МНК по данным из табл. 1

141

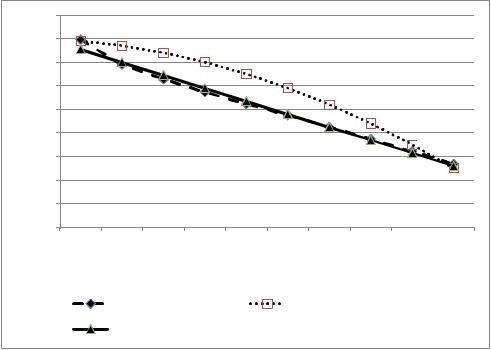
Рис. 2. Значения оценок критериев, полученные аддитивным методам, а также методом Раша, основанным на МП-методе и МНК по данным из табл. 1

Из рис. 1 и 2. видно, что модель Раша, основанная на МП-методе, как и ожидалось, дает абсолютно линейные оценки. Но более важно то, что модель Раша, основанная на МНК, дает практически линейные оценки с малой нелинейностью в концах измерительного интервала латентных переменных. Эта особенность была предположена для оценок, отличных от МП-метода Раша в работе [7], где и отмечалось, что если будет наблюдаться нелинейность оценок, то она будет в рамках погрешности измерений. Данное исследование подтвердило выдвинутое предположение. Можно сказать, что обнаруженная нелинейность оценок не оказывает существенного влияния на характер распределения оценок латентных переменных в первом приближении, хотя бы с точки зрения, что эти переменные латентные, то есть не детерминированные.

В то же время аддитивный метод, применяемый традиционно для решения задач оценивания латентных параметров, показывает существенную нелинейность полученных оценок, что может привести к искажению результата при оценивании латентных показателей.

Заключение

Из всего этого можно сделать выводы о том, что результаты проведенного вычислительного эксперимента подтверждают линейность оценок латентных переменных, проведенных по классической модели Раша, основанного на МП-методе. Метод Раша, основанный на МНК, дает квазилинейные оценки, величина отклонения от линейности для которых невелика и укладывается в рамки погрешности модели при обработке информации, представленной от измерения индикаторных переменных. В то же время, оценки, полученные при расчете по аддитивной модели, дают существенное отклонение от линейности.

Таким образом, оценки латентных переменных, осуществленные по модели Раша, основанной на МНК, можно рекомендовать для практического применения с сохранения

142

всех достоинств классической модели Раша, полагая, что эта модель дает линейные (квазилинейные) и адекватные оценки.

Библиографический список

1.Маслак А.А. Модель Раша оценки латентных переменных и ее свойства. Монография / А.А. Маслак, С.И. Моисеев. – Воронеж: НПЦ «Научная книга», 2016. – 177 с.

2.Маслак А.А. Сравнительный анализ оценок параметров модели Раша, полученных методами максимального правдоподобия и наименьших квадратов / А.А. Маслак, С.И. Моисеев, С.А. Осипов. — Проблемы управления, № 5, 2015. — С. 58-66.

3.Баркалов С.А. Применение метода наименьших квадратов при оценке латентных переменных методом Раша / С.А. Баркалов, С.И. Моисеев, Е.В. Соловьева // Научный вестник Воронежского ГАСУ. Сер. «Управление строительством». – 2014. – Вып. № 1 (6). −

С.112-115.

4.Моисеев С.И. Методы принятия оптимальных решений: учеб. пособие / С.И. Моисеев, А.А. Зайцев. - Воронеж: АОНО ВО «Институт менеджмента, маркетинга и финансов», 2016 .- 144 с.

5.Маслак А.А. Измерение латентных переменных в социально-экономических системах: Монография. – Славянск-на-Кубани: Изд. Центр СГПИ, 2006.

6.Моисеев С.И. Модель Раша оценки латентных переменных, основанная на методе наименьших квадратов / Экономика и менеджмент систем управления. Научно-практический журнал. № 2.1 (16), 2015. — С. 166-172.

7.Goodman, L.A. Explanationary Latent Structure Analysis Using Both Identifiable and Unidentifiable Models / L.A. Goodman // Biometrika.-1974.-Vol.61.- № 2

143

УДК 629.7.0.001.2.015.017.2:519.6:62-50

ОБ УСТОЙЧИВОСТИ САМОЛЕТА С АВТОМАТИЧЕСКОЙ СИСТЕМОЙ РУЧНОГО УПРАВЛЕНИЯ ПРЕДСТАВИМОГО УРАВНЕНИЕМ РАЗРЕШЕННЫМ ОТНОСИТЕЛЬНО ПРОИЗВОДНЫХ С ШИРОКИМИ НАЧАЛЬНЫМИ УСЛОВИЯМИ

П.А. Котов НИИ математики, Россия, Воронеж

Рассматривается вещественный вариант динамической модели «самолет-автопилот» описываемый конечномерным уравнением с линейным суммируемым дифференциальным оператором, постоянными положительными элементами коэффициентной системы, измеримыми начальными условиями и предлагаются конструктивные аспекты устойчивости.

ABOUT THE STABILITY OF THE aircraft WITH THE AUTOMATIC MANAGEMENT SYSTEM OF THE PRESENT EQUATION OF THE PERMITTED RELATIVE TO THE DERIVATIVES WITH WIDE INITIAL CONDITIONS

P.A. Kotov

Research institute mathematics, Russia, Voroneg

Тhe real version of the dynamic model "aircraft-autopilot", described by a finite-dimensional equation with a linear summable differential operator, constant positive elements of the coefficient system, measurable the initial conditions is considered and the constructive aspects of stability are offered.

Введение

Расширение эксплуатационного диапазона скоростей и высот полета современных маневренных самолетов потребовало внедрения автоматизации систем ручного управления для обеспечения безопасности полетов и повышения их эффективности.

При проектировании автоматизированных систем управления возникают задачи взаимодействия системы управления с самолетом как с динамической системой в замкнутом контуре управления. Решение таких задач производится, как правило, на пилотажных стендах или специальных моделирующих установках. Уравнения движения самолета решаются на ЭВМ, а реальная система управления при этом может быть заменена математической моделью, полунатурным макетом и т.п. в зависимости от постановки задачи [1].

С помощью приобретенного опыта компьютерного моделирования автономных сложных систем объединяющих разнотипные подсистемы, описываемых линейными вещественными уравнениями, автор настоящей работы предлагает содержательный подход исследования устойчивости динамических систем с включением основ вещественных дифференциальных уравнений, технической теории устойчивости движения, теории систем автоматического регулирования [2].

Одним из важнейших аспектов работоспособности системы автоматического управления является устойчивость. Система, не обладающая устойчивостью, вообще не способна выполнять функции управления. Неустойчивая система может привести

© Глущенко А.И., Петров В.А., Ласточкин К.А., 2018

144

управляемый объект в аварийное состояние. Поэтому, проблема устойчивости системы автоматического управления является одной из центральных в теории автоматического управления. Понятие устойчивости системы регулирования связано со способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния [3].

В авиации устойчивость характеризует способность самолета без вмешательства пилота сохранять заданный режим полета [Устойчивость. Электронный ресурс.2017].

Научный интерес вызван исследованиями устойчивости «самолет-автопилот» представимого линейным уравнением шестого порядка разрешенным относительно производных с постоянными элементами коэффициентной системы, измеримыми начальными условиями из широкого массива скалярных начальных условий.

п.1 О решении вещественного линейного конечномерного уравнения с заданными начальными условиями и теоретических аспектах устойчивости.

Пусть безрезонансный вариант динамической модели объекта управления описывается конечномерным уравнением в нормальной форме шестого порядка с линейным суммируемым дифференциальным оператором:

автоматического регулирования представимой конечномерным уравнением разрешенным относительно производных сводится к исследованию общего решения оговариваемого уравнения с заданными начальными условиями на неотрицательной полупрямой оси времени фиксированной ориентации. Важными представляются исследования общего решения вещественного уравнения (1) с постоянными положительными элементами коэффициентной системы, измеримыми начальными условиями (2) при нулевом начальном отсчете времени [4]. Известный подход решения обыкновенного дифференциального уравнения приведен в опубликованных библиографических источниках [4,5,6]. Строгое математическое определение устойчивости динамической системы связано с определением устойчивости решения дифференциального уравнения [5]. Это определение было сформулировано А.М. Ляпуновым.

Пусть начальные возмущения, прикладываемые к системе в момент времени t=t0, ограничиваются малой областью ( ) . Тогда система называется устойчивой по

ляпунову, если при t t0 отклонение возмущенного движения от невозмущенного, так же сколь угодно мало и ограничивается областью , иными словами, близкие по начальным

условиям решения остаются близкими и при t t0 . Система называется асимптотически

устойчивой, если 0 при t . Здесь автор настоящей работы выделяет важность развития отклонения движений, поведения близких решений на полупрямой оси времени предполагаемых асимптотически устойчивых ответственных систем при различных опытных начальных условиях, поскольку на некоторых аргументных отрезках оговариваемые отклонения могут изменяться непредвиденным образом, тогда как при

больших значениях аргумента непрерывно приближаться в пределах произвольной

145

невозрастающей функции с 0 при t . Об этом сегодня умалчивается в отечественных научных изданиях, как и о внимании к развитию отклонения искомых

движений в ограниченной фиксированной области . близость решений подробно не изучается, полагают, что близкие по начальным условиям решения остаются близкими и

при t t0 . К примеру, близость может выделяться биениями на отрезках полупрямой оси времени, колебаниями, выбросами, сложным поведением ограниченной выходной

переменной в пределах различно изменяемой области .

В обстоятельных исследованиях устойчивости ответственных систем учитывать характер поведения отклонения решений с изучением развития близких решений с опытными

начальными условиями в изменяемой искомой ограниченной области ,

знакоопределенность скорости убывания при достижении требуемой .

Известны основы когда линейная система, находящаяся под воздействием внешней силы F(t) , описывается неоднородным дифференциальным уравнением:

однородного уравнения (5), характеризующее свободные колебания в системе; Сi -

постоянные коэффициенты, определяемые из начальных условий, pi - корни характеристического уравнения (6) действительные и комплексные.

Если все действительные корни и действительные части комплексных корней pi

возмущениях [5]. Поэтому, такая системы, согласно определению Ляпунова, является асимптотически устойчивой.

п.2 Об испытаниях динамической модели исходной конечномерной системы ресурсами лэптопа с широким массивом начальных условий.

146

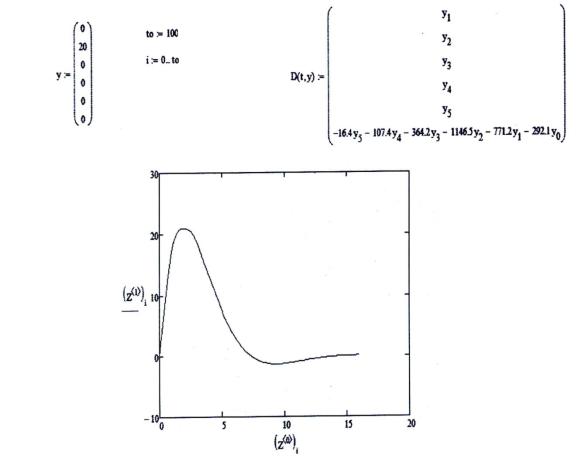
Выходной массив моделирования испытываемого варианта модели системы «самолет с автопилотом», описываемого вещественным нормальным уравнением с линейным суммируемым дифференциальным оператором, постоянными скалярными начальными условиями [2]:

удовлетворяющего необходимым и достаточным условиям устойчивости на основании алгебраического критерия устойчивости Гурвица отличающийся технической устойчивостью [Карачаров К.А. и Пилютик А.Г. Введение в техническую теорию устойчивости движения. М., Физматгиз.1962.-244с.] представлен на рис.1 информативного выходного массива моделирования содержащего график поведения выходной переменной полученного численным методом из пакета программ matlab с заданными начальными условиями (9). Изменение значений определителей матрицы Гурвица в зависимости от порядка стремящегося к порядку исходного уравнения имело вид возрастающей знакопостоянной функции.

Рисунок 1. информативный выходной массив моделирования

При ненулевых начальных значениях скорости в 20 единиц, ускорения в 100 единиц и остальных нулевых начальных значениях

147

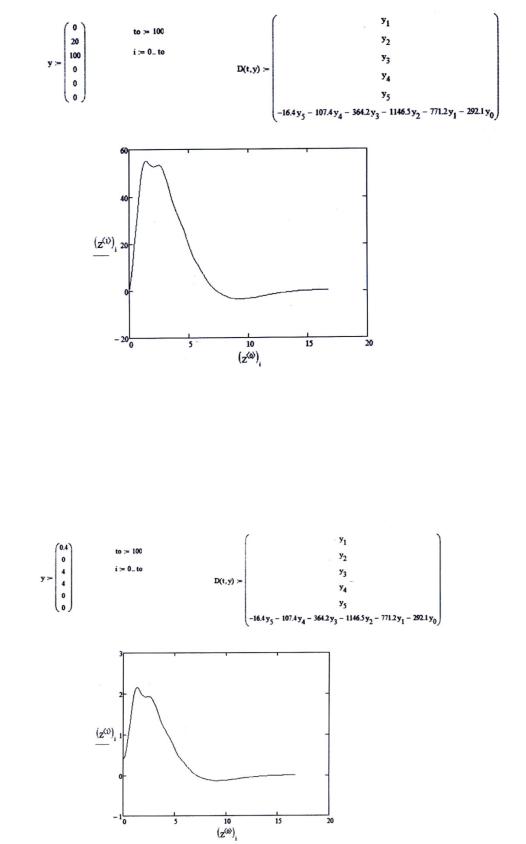
возникали особенности в поведении выходной переменой в верхнем подмножестве результативного множества выходных значений, что приведено на рис.2 информативного выходного массива моделировании ресурсами личного переносного компьютера

Рисунок 2. информативный выходной массив моделирования

Отмечаемые нарушения в поведении выходной переменной в сравнении с предыдущим испытанием говорят о возможных нарушениях диагностируемого состояния, опасных моментах для системы.

При других начальных условиях возникали нарушения в верхнем подмножестве результативного множества выходной переменной, что отражено на рис. 3,4 информативного выходного массива моделирования

Рисунок 3. информативный выходной массив моделирования

148

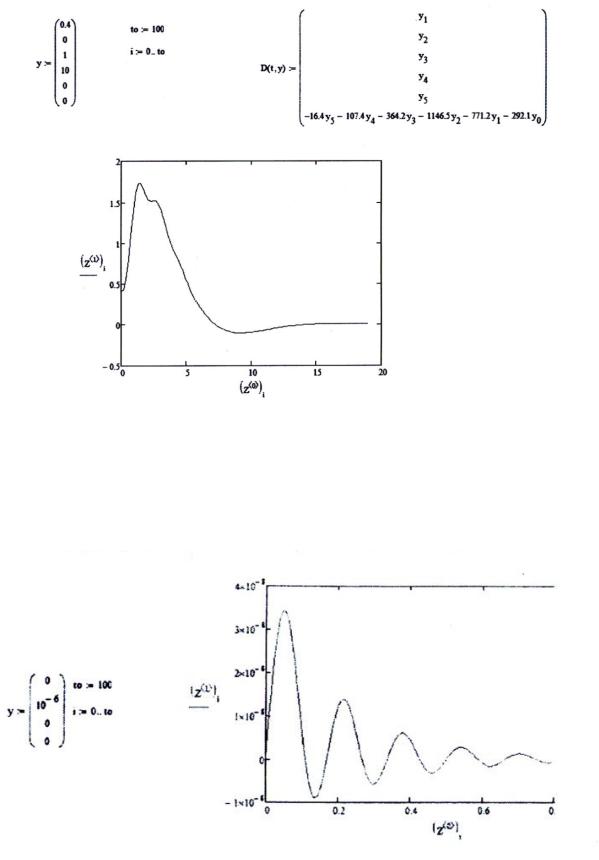
Рисунок 4. информативный выходной массив моделирования

При испытаниях динамической модели электрогидравлической следящей системы [2],

описываемой уравнением: y(4) 103y(3) 3065y 149250y 1081500y 0

получены следующие информативные выходные массивы моделирования, представленные на рис. 5,6 с выраженным изменением выходной переменной затухающей на бесконечности:

Рис. 5

149

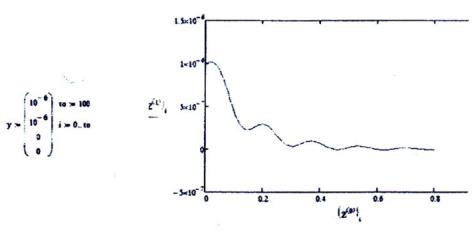
Рис.6

Утверждение. Об устойчивости детерминированного варианта конечномерной сложной системы описываемого уравнением разрешенным относительно производных с линейным суммируемым дифференциальным оператором, фиксированными элементами полной коэффициентной системы, опытными начальными условиями при отличии собственных частот колебаний от частот начальных возмущений вырабатывать мнения по поведению выходной переменной действительного однородного уравнения на полупрямой оси времени t с наблюдаемым зафиксированным началом

отсчета t0 при t t0 .

Предлагаемые конструктивные аспекты устойчивости сложных систем учитывать также в исследованиях точности и работоспособности автономных систем ориентации и стабилизации маневренных изделий и аппаратов.

В качестве достаточных условий устойчивости предлагается считать следующее: Ограниченно непрерывные отклонения искомых решений линейного уравнения разрешенного относительно производных с собственными частотами колебаний отличных от частот начальных возмущений.

Библиографический список

1.Клумов А.С. Продольная устойчивость и управляемость маневренного самолета.-М.: Машиностроение, 1988.-200с.

2.Котов П.А. Особенности устойчивости конечномерной системы описываемой безрезонансным уравнением с линейным дифференциальным оператором// Моделирование систем и процессов.2016,т.9, вып.2.-С.42-51

3.Бесеверский В.А., Попов Е.П. Теория систем автоматического регулирования. Издание третье, исправленное.М.:Наука. Гл.ред.физ. – мат.лит.1975.-768с.

4.Краснов М.Л. Обыкновенные дифференциальные уравнения: Учеб. пособие для втузов.-М.: Высш. школа.1983.-128с.

5.Каганов В.И. Системы автоматического регулирования в радиопередатчиках-М., Связь, 1969.-232с.

6.Степанов В.В. Курс дифференциальных уравнений: Учеб. для государственных университетов. – Издание восьмое стереотипное.-М. Государств. издательство физикоматематической литературы.1959.-468с.

150