Учебное пособие 800628

Библиографический список

1.Красилов В.А. Нерешённые вопросы теории эволюции. – Владивосток: ДВНЦ АН

СССР, 1986. 138 с.

2.Подвальный С.Л. Многоальтернативные системы: обзор и классификация // Системы управления и информационные технологии. 2012. Т. 48, № 2. С. 4-13.

3.Подвальный С.Л., Васильев Е.М. Многоальтернативное управление открытыми системами: концепция, состояние и перспективы // Управление большими системами: сб. тр. ИПУ РАН. 2014. № 48. С. 6-58.

4.Подвальный С.Л., Васильев Е.М. Концепция многоальтернативности в живых и неживых структурах // Онтология проектирования. 2016. Т.6, №3(21). С. 355-367.

5.Филимонов Н.Б. Методологический кризис «всепобеждающей математизации» современной теории управления // Мехатроника, автоматизация, управление. 2016. Т. 17, №

5.С. 291–300.

6.Подвальный С.Л., Васильев Е.М. Биологическое разнообразие и модели эволюции //

Вестник Воронежского государственного университета инженерных технологий. 2016. № 3 (69). С. 123-127.

7.Подвальный С.Л., Васильев Е.М. Влияние биологического разнообразия на эволюционную устойчивость экологических систем // В сб.: Комплексные проблемы техносферной безопасности. Материалы Междунар. научно-практ. конф. Воронеж: ВГТУ, 2017. С. 4-7.

8.Подвальный С.Л., Васильев Е.М. Моделирование эволюционных процессов биологических систем // В сб.: Современные методы прикладной математики, теории управления и компьютерных технологий (ПМТУКТ-2016). Сб. тр. IX междунар. конф. Воронеж: Научная книга, 2016. С. 271-274.

9.Колесников А.А. Синергетическая теория управления: концепция, методы, тенденции развития // Известия Южного федерального университета. Технические науки. 2001. Т. 23, № 5. С. 7-27.

10.Подвальный С.Л., Васильев Е.М. Cинергетические свойства принципов многоальтернативности // В сб.: Современные методы прикладной математики, теории управления и компьютерных технологий (ПМТУКТ-2017). Сб. тр. X междунар. конф. Воронеж: Научная книга, 2017. С. 289-292.

11.Колмогоров А.Н. Три подхода к определению понятия “количество информации”

//Проблемы передачи информации. 1965. Т. 1, вып. 1. –С. 3–11.

131

УДК 021.8+025.1

ЗАДАЧА ВЫБОРА ОПТИМАЛЬНОГО СПЕКТРА ПО ЗАДАННОЙ ТОЧНОСТИ СХОДИМОСТИ ВЫХОДА СИСТЕМЫ

Н.В. Берсенев Институт проблем управления им. В.А. Трапезникова РАН, Москва

Рассматривается задача выбора спектра в линейной системе со скалярным входом и выходом и неизвестными возмущениями. Требуется заданная точность сходимости выхода системы. Критерием выбора является минимизация нормы матрицы обратной связи. Предложенный алгоритм выбора спектра проиллюстрирован на примерах простых систем второго порядка.

THE PROBLEM OF CHOICE OF OPTIMAL SPECTRUM FOR GIVEN ACCURACY OF

OUTPUT OF THE SYSTEM FOR SECOND-ORDER SYSTEMS.

N. Bersenev,

Institute of Control Sciences of RAS

In present paper we consider the problem of choosing the spectrum of linear SISO system with unknown limited disturbances. Accuracy of convergence for output of system is assumed to be given. The criterion of this choice is assumed to be a minimization of norm of feedback matrix. The proposed algorithm for choosing a spectrum is illustrated by examples of simple second-order systems.

Введение

Классическая задача модального управления состоит в назначении заданного спектра замкнутой системы с помощью обратной связи. Несмотря на огромное количество работ, посвященной этой давно известной задаче, алгоритма выбора собственных значений замкнутой системы не существует, и на практике они часто определяются экспериментально.

В данной работе ставится задача выбора спектра при заданной точности выхода системы. При этом минимизируется норма Фробениуса матрицы обратной связи.

Работа имеет следующую структуру. В разделе 2 приведён алгоритм выбора спектра для произвольной SISO-системы второго порядка, в разделе 3 работа этого алгоритма проиллюстрирована на двух частных примерах. Раздел 4 – заключение.

Алгоритм

2.1.ПОСТАНОВКА ЗАДАЧИ

Рассматривается математическая модель линейной стационарной системы со

скалярными входом и выходом вида:

где x, u – векторы состояния и управления, A, Q – матрицы с постоянными коэффициентами соответствующих размерностей, пара (A,bT ) – управляема.

Ставится задача стабилизации системы (1) с помощью линейной обратной связи

(2) u Fx,

© Берсенев Н.В., 2018

132

при заданной – точности сходимости выхода системы

(3) T 0, t T : y(t) .

Применительно к такой системе ставится задача минимизации критерия

(4) F tr(FFT ) min.

2.2.АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СЛУЧАЯ 2-ГО ПОРЯДКА

Рассмотрим систему второго порядка со скалярным управлением и выходом и

неизвестными возмущениями общего вида.

(5)x&1 a11x1 a12x2 q11 1 q12 2 ,

x& 2 a21x1 a22x2 bf1x1 bf2x2 q21 1 q22 2.

Блочным методом назначим управление для некоторых комплексных собственных значений замкнутой системы. Сделаем замену переменных:

(6) x2 a11a 1 x1 x2 , 12

С помощью выбора обратной связи приведем систему к верхне треугольному виду.

Тогда компоненты матрицы обратной связи F будут иметь вид:

bf2 1 2 a11 a22.

Точность сходимости вектора состояния и выхода системы может быть представлена в виде:

x2 q21 1 q22 2 ,

Re 2

при ограничении (9).

Примеры

Проиллюстрируем приведенный алгоритм на двух частных примерах:

3.1.ПРИМЕР 1

Рассмотрим систему

Согласно (8):

133

F 563.

0,1: спектр замкнутой системы 1 9,12; 2 68,4. Норма матрицы обратной связи

F 7850.

0,05: спектр замкнутой системы 1 8,93; 2 138. Норма матрицы обратной связи

F 29850.

Заключение

В данной работе предложен алгоритм нахождения оптимальной в смысле экономии ресурсов управления обратной связи для SISO-системы с неизвестными возмущениями при заданной точности выхода. Спектр замкнутой системы назначается автоматически в ходе процедуры оптимизации. Особенностью предлагаемого подхода является декомпозиция задачи на подзадачи меньших размерностей и последовательное назначение корней в каждой из них. Эффективность разработанных алгоритмов оптимизации продемонстрирована на численных примерах.

Библиографический список

1.DAVISON E. On pole assignment in linear systems with incomplete state feedback // IEEE Trans. on Automat. Control. 1970. V AC-15. N6. P. 348-351.

2.ЦВИРКУН А. Д. Основы синтеза структуры сложных систем. – М.: Наука, 1997.

3.Андреев Ю.Н. Управление конечномерными линейными объектами. – М.: Наука,

1976.

4.Кочетков С.А., Уткин В.А. Минимизация нормы матрицы обратной связи в задачах модального управления // Автомат. и телемех. 2014. №2. 72-105.

5.ПОЛЯК Б., СМИРНОВ Г. Большие отклонения в линейных системах при ненулевых начальных условиях // Автомат. и телемех. 2015. №6. 18-41.

134

УДК 519.1

ДИНАМИКА ГРАФОВ СОЦИАЛЬНЫХ СЕТЕЙ, ПОСТРОЕННЫХ ПО АЛГОРИТМУ С ОТСЕВОМ АКТИВНЫХ УЗЛОВ

А.А. Гилязова, Д.Н. Федянин ФГБУН Институт проблем управления им. В.А. Трапезникова РАН, Москва

В работе представлены результаты анализа динамики параметров растущих сетей, построенных по алгоритму с отсевом активных узлов и имитирующих свойства онлайновых социальных сетей.

DYNAMICS OF THE GRAPHS OF SOCIAL NETWORKS GENERATED USING AN ALGORITHM WITH NODES DEACTIVATION

A. Giliazova, D. Fedyanin

Institute of Control Sciences of RAS

This article contains the results of modelling growing graphs of social networks using the algorithm with nodes deactivation. The results are compared with the parameters of Russianlanguage segment of Facebook.

1.Введение

Данная работа продолжает исследование алгоритма с отсевом активных узлов, представленного в работе [2] и предназначенного для моделирования графов социальных сетей (см. обзор других известных моделей в [3], [4]). Предыдущие исследования показали [1], что рассматриваемый алгоритм позволяет достичь приближения одновременно к системе требуемых статистических характеристик, а в частности: степенное распределение степеней вершин, положительная ассортативность.

В данной работе исследуются изменения параметров в процессе роста такой сети, а также было проведено сравнение с характеристиками русскоязычного сегмента онлайновой социальной сети Facebook. Обезличенные данные об этой социальной сети были предоставлены компанией «Лаборатория цифрового общества» (www.digsolab.com). Как показано в [5], структура онлайновых социальных сетей схожа с оффлайновыми.

Одно из предполагаемых практических направлений использования результатов данного исследования состоит в генерации графов малого размера, обладающих статистическими свойствами, аналогичными реальным социальным сетям, что было бы удобно для использования, например, в моделировании процессов распространения информации в таких сетях. Кроме того, модель может представлять теоретический интерес для объяснения механизмов роста социальных сетей, прогнозирования их дальнейшей динамики, оценки устойчивости и возможностей управления.

2.Описание алгоритма

Входными данными алгоритма являются значения следующих параметров: Z – число новых активных узлов на каждом шаге,

P – вероятность образования новой связи активным узлом,

G – доля активных узлов, отсеиваемых на каждом шаге,

N – требуемое количество связанных узлов, по достижении или превышении которого работа алгоритма останавливается.

© Гилязова А. А., Федянин Д.Н., 2018

135

При построении графа происходит циклическое повторение следующей процедуры до тех пор, пока граф не достигнет требуемого количества узлов.

1) В сеть добавляется Z n новых активных узлов, т.е. счётчики числа узлов и числа активных узлов увеличиваются на Z.

2)Каждый из активных узлов с вероятностью P (0,1] генерирует ненаправленную связь с одним из прочих активных узлов, выбранным случайным образом. Информация о связях может храниться, например, в виде матрицы смежности графа.

3)Доля G (0,1) активных узлов, выбранных с вероятностью, обратно пропорциональной числу их связей, включая петли, теряет статус активных. При этом узлы и их связи сохраняются в сети, меняется только статус активности, влияющий на образование новых связей.

При расчёте степеней узлов для целей вычисления вероятностей отсева учитываются петли, т.е. все узлы имеют связь с самими собой и их степень не ниже единицы, что предотвращает вероятность деления на нуль при расчёте обратно пропорциональных величин. Но при вычислении общего числа связей в графе, средней степени узлов, плотности графа петли отбрасываются.

Параметры алгоритма в данной работе. На каждом шаге в сеть добавляется 25 новых активных узлов. Далее 5% активных узлов образуют новые связи (округление вверх, чтобы не ухудшать связность графа из-за погрешностей). Поскольку связи ненаправленные, то это означает, что на каждом шаге у 10% активных узлов степень увеличивается на единицу. Далее на стадии отсева деактивируется 5% активных узлов (это число округляется вниз) с вероятностью, обратно пропорциональной их степени. Эта вероятность рассчитывается для всех узлов в начале стадии отсева и далее не пересчитывается, таким образом на неё не влияет порядок, в котором отсеиваются узлы.

Выходные данные: граф, построенный в соответствии с указанными значениями параметров.

3.Результаты расчётов

Для оценки диапазона случайного разброса получаемых результатов было выполнено 5 запусков с идентичными начальными параметрами. Для оценки изменений, происходящих в сети в процессе её роста, значения параметров рассчитывались не только для итогового графа, но также и по достижении сетью следующего числа узлов: 250, 2 500, 25 000. Для расчёта части параметров использовалась программа Gephi 0.9.1.

Полученный граф имеет 250 000 связанных узлов. Число связей случайно варьировалось при разных запусках в диапазоне от 1 157 064 до 1 162 100 связей. Для сравнения, в русскоязычном сегменте онлайновой социальной сети Facebook в сентябре 2013 года имелось примерно 3,25 млн. пользователей и около 155,28 млн. связей.

Средняя степень узлов в полученном графе составляет примерно 4,6, что на порядок меньше, чем в русскоязычном сегменте онлайновой социальной сети Facebook (47,8). Тем не менее, по мере роста сети этот показатель увеличился с 1,7…1,8, что говорит о том, что данное отличие может быть обусловлено именно разницей размеров сетей и выбранными начальными параметрами, а не ограничениями модели.

Максимальная степень узла по мере роста сети увеличилась с 6…9 до 1 722…2 081, что существенно лучше в сравнении с предыдущими исследованиями сетей размером 10 000 узлов. В русскоязычном сегменте онлайновой социальной сети Facebook этот показатель составлял 4 199.

Плотность в процессе роста сети уменьшилась с (6,6…7,2) ∙10-3 до (1,6…1,9) ∙10-5. Для русскоязычного сегмента Facebook плотность составляла 1,5∙10-5, т.е. по этому показателю достигнута близость, что также существенно лучше, в сравнении с сетями 10 000 узлов.

136

Доля гигантской компоненты в процессе роста сети увеличилась с 0,46…0,65 до 0,95…0,96. В реальных социальных сетях она превышает 0,9. Таким образом, здесь достигнуто целевое значение, причём не позднее чем в сети размером 2 500 узлов.

Средний коэффициент кластеризации составил 0,021…0,022. Число треугольников 113 231…127 448.

Одна из особенностей модели состоит в том, что довольно большое число узлов может быть отсеянным до того, как они образуют хотя бы одну связь, и остаться изолированными. Предположительно, это может отражать некоторые процессы в реальных социальных сетях, поскольку пользователи могут зарегистрироваться, но в дальнейшем не участвовать в социальной сети. В данной работе не учитываются изолированные узлы, полученные в количестве 328 950…331 475 сверх выше упомянутых 250 000 узлов, каждый из которых имеет хотя бы одну связь.

Другая особенность модели с линейным ростом и фиксированной долей отсева состоит в том, что число активных узлов остаётся постоянным, после достижения некоторого значения. Таким образом, в данной модели у сети есть чётко выраженная стадия активного роста, когда число активных узлов увеличивается, и стадия зрелости, когда общее число узлов продолжает увеличиваться, но число активных узлов остаётся постоянным. В сети с заданными начальными параметрами одновременно может быть не более 500 активных узлов, и это значение достигается при размере сети 250 000. Для 2 500 и 25 000 узлов в сети имелось 475 активных узлов, а в сети 250 узлов, имеющих хотя бы одну связь, находилось 320 активных узлов, включая изолированные.

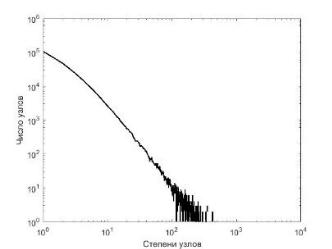
Одним из ключевых моделируемых параметров является показатель степени степенного распределения степеней вершин, характеризующий степень наклона прямой в логарифмических координатах (см. Рис. 1). В данной работе он рассчитывался без учёта зашумлённой правой части графика. В реальных социальных сетях этот показатель считается примерно равным -2,1. В данной сети по мере её роста этот показатель сначала увеличивался в требуемом направлении с -3,03…-2,42 до -2,32… -2,18, а затем уменьшился до -2,52…-2,46. Тем не менее, значение показателя довольно близкое к целевому, и может быть улучшено за счёт изменения начальных параметров.

Рис. 1. Распределение степеней узлов итогового графа в логарифмическом масштабе

Другой ключевой показатель – коэффициент ассортативности, положительное значение которого означает, что со статистической точки зрения люди более склонны иметь друзей, у которых примерно то же количество друзей. Одно из возможных объяснений данного эффекта состоит в том, что если у человека есть друг с большим числом друзей, то он может его с ними познакомить, и тогда у них обоих будет большое число друзей. Для

137

русскоязычного сегмента онлайновой социальной сети Facebook коэффициент ассортативности оценивался как примерно 0,3. В данной сети по мере её роста коэффициент ассортативности сперва увеличивался с 0,15…0,25 до 0,33…0,36, а затем снова уменьшился, составив в итоговой сети 0,07…0,09.

Это единственное обнаруженное ухудшение качества моделирования при увеличении размера сети, причина которого требует дальнейшего исследования и может быть связана с обозначенным ранее переходом к зрелой стадии сети. Если это так, то вероятно, более точных результатов можно будет достичь, заменив линейный рост сети на ускоренный, с тем, чтобы рост числа активных узлов не прекращался и зрелая стадия не наступала. Тем не менее, коэффициент ассортативности, по крайней мере, остался положительным. Кроме того, несмотря на то, что известные крупные социальные сети росли ускоренно, а не линейно, очевидно, что такой рост не может продолжаться бесконечно, т.к. население земного шара растёт менее быстрыми темпами. В связи с этим можно ожидать для этих социальных сетей замедление темпов роста. В этом случае возможно, что модели с ускоренным ростом могут лучше описать нынешние характеристики этих сетей, но модели с линейным ростом дадут более точный прогноз их будущей динамики. Также такие модели могут в ряде случаев быть применены, например, к социальным сетям внутри организаций.

Библиографический список

1.ГИЛЯЗОВА А.А. Моделирование графов социальных сетей большого размера

//Теория активных систем (ТАС-2016): Труды международной научно-практической конференции — М.: ИПУ РАН, 2016. — С. 247-250. — Электронная версия доступна по адресу: http://www.mtas.ru/seminar/tas2016

2.ГИЛЯЗОВА А.А. О новом алгоритме построения графов, обладающих статистическими характеристиками, схожими с реальными социальными сетями // Теория активных систем (ТАС-2014) — М.: ИПУ РАН, 2014. — С. 201-202. — Электронная версия доступна по адресу: http://www.mtas.ru/search/search_results.php?publication_id=19832

3.РАЙГОРОДСКИЙ А.М. Модели случайных графов. — М.: МНЦМО, 2011. — 136 с. — Электронная версия доступна по адресу: http://www.mccme.ru/free- books/dubna/raigor-4.pdf

4.BELL M., PERERA S., PIRAVEENAN M., BLEMER M., LATTY T., REID C. Network growth models: A behavioural basis for attachment proportional to fitness // Scientific reports 7, Article number: 42431 (2017). – https://www.nature.com/articles/srep42431

5.DUNBAR R.I.M., ARNABOLDI V., CONTI M., PASSARELLA A. The structure of online social networks mirrors those in the offline world // Social networks, Volume 43, October 2015, pp. 39-47. https://doi.org/10.1016/j.socnet.2015.04.005.

138

УДК 303.714

ИССЛЕДОВАНИЕ ЛИНЕЙНОСТИ ОЦЕНОК ЛАТЕНТНЫХ ПЕРЕМЕННЫХ, ВЫЧИСЛЕННЫХ ПО МОДЕЛИ РАША

В.С. Кобелев, С.И. Моисеев

Воронежский государственный технический университет

В статье проверяется свойство линейности оценок латентных переменных, полученных по модели Раша. Показано, что модель Раша, основанная на методе максимального правдоподобия дает линейные оценки. Модель Раша, основанная на методе наименьших квадратов имеет несущественную нелинейность. Традиционная аддитивная модель дает нелинейные оценки.

LINEARITY INVESTIGATION OF LATENT VARIABLES ESTIMATES

CALCULATED BY THE RASCH MODEL

V. S. Kobelev, S. I. Moiseev

The linearity property of latent variables estimates obtained by the Rasch model is checked in the article. It is shown that the Rasch model based on the maximum likelihood estimation yields linear estimates. The Rasch model, based on the method of least squares, has an insignificant nonlinearity. The traditional additive model gives nonlinear estimates.

Модель Раша оценки латентных переменных [1] в последнее время используется все чаще в различных сферах научной и практической деятельности для оценки неявных показателей.

Одно из преимуществ оценивания по модели Раша состоит в том, что оценки получаются по линейной интервальной шкале, что удобно для сравнения результатов оценивания и проведения различного рода статистических процедур. Свойство линейности оценок по классической модели Раша не вызывает сомнений [2], т.к. оно заложено в математическом ядре получения оценок, а именно на методе максимального правдоподобия (МП-метод).

Однако, в последнее время большую популярность набирает модификация модели Раша, которая основана на методе наименьших квадратов (МНК), которая позволяет использовать исходные данные непрерывного типа для оценивания [3]. Но для этой модели линейность оценок не доказана теоретически, поэтому возникает резонный интерес по этому вопросу: являются ли оценки по МНК линейными, и если нет, то насколько ощутима эта нелинейность? Кроме этого интересно проанализировать, насколько нелинейны оценки по традиционной модели оценивания, которые получаются простым сложением или усреднением частных оценок (назовем это аддитивной моделью оценивания).

Постановка задачи

В работе ставится задача методами математического моделирования и вычислительных экспериментов проверить линейность оценок и оценить степень их нелинейности для:

© Кобелев В.С., Моисеев С.И., 2018

139

1)модели Раша, основанной на МНК;

2)модели Раша, основанного на МП-методе;

3)аддитивного метода оценивания.

Теоретические основы оценивания латентных переменных по разным методам

Приведем кратко методики получения оценок латентных переменных, проведенные по аддитивному методу, модели Раша, основанной на МП-методе и основанной на МНК.

Пусть имеется n объектов, латентный показатель которых подлежит оценке. Оценивание проводится на основе k индикаторных переменных. Имеем матрицу индикаторных переменных, нормированных на единичную шкалу, то есть обозначим через

uij - оценку i-го объекта по j-ой индикаторной переменной.

1.Оценки по аддитивному методу. Итоговые оценки латентных переменных каждого объекта i вычисляются по формулам [4]:

kj 1

2.Классический метод Раша, основанный на МП-методе. Введем следующие латентные переменные:

i –оценка латентного показателя для i-го объекта Ai;

βj - степень невыполнимости индикаторной переменной: тем меньше ее значение, тем больше все объекты с точки зрения индикаторной переменной ей удовлетворяют.

В такой модели вероятность pij того, что по j-ой индикаторной переменной оценка i-го объекта будет выше, чем степень невыполнимости индикаторной переменной βj будет определяться логистической функцией [5]:

нахождения численного решения используют специальное программное обеспечение, например программу RAMM 2020.

3. Метод Раша, основанный на МНК. Латентные переменные задаются так же, как и в предыдущем методе, но для нахождения латентных переменных i и j решается оптимизационная задача вида [6]:

Проверка линейности оценок

Другой подход к проверке адекватности модели заключается в следующем. Формируется матрица индикаторных переменных, которая должна давать линейные оценки латентных переменных.

Согласно [5], эта матрица должна давать пропорциональный рост значений индикаторных переменных с номером строки и номера столба. Если взять, для примера, 10 объектов, латентные переменные которых оцениваются с помощью 10 индикаторных переменных, то матрица значений индикаторных переменных uij должна быть симметричной

140