3. Решение невырожденных линейных систем. Формулы Крамера

Пусть дана система линейных уравнений с неизвестными

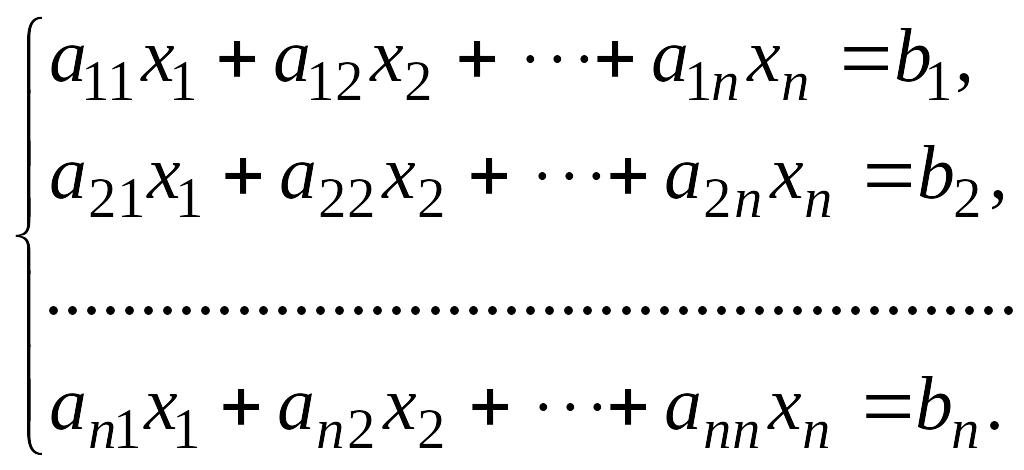
или в матричной форме .

Основная матрица такой системы квадратная. Определитель этой матрицы

.

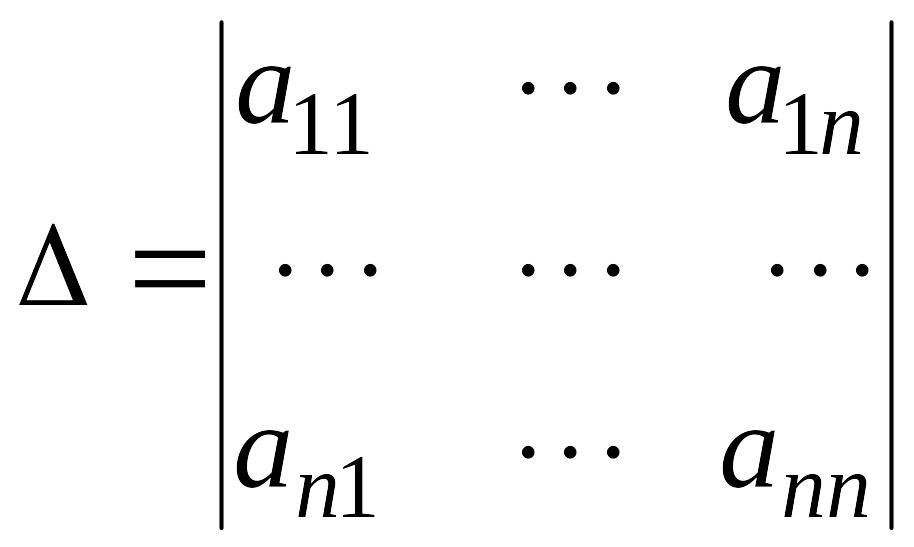называется определителем системы. Если определитель системы от­личен от нуля, то система называется невырожденной.

Найдем решений данной системы уравнений в случае .

Умножив обе части уравнения слева на матрицу , получим . Поскольку и ,

. (4.1)

Определение. Отыскание решения системы по формуле (4.1) называют матрич­ным способом решения системы.

Матричное равенство запишем в виде

,

то есть

.

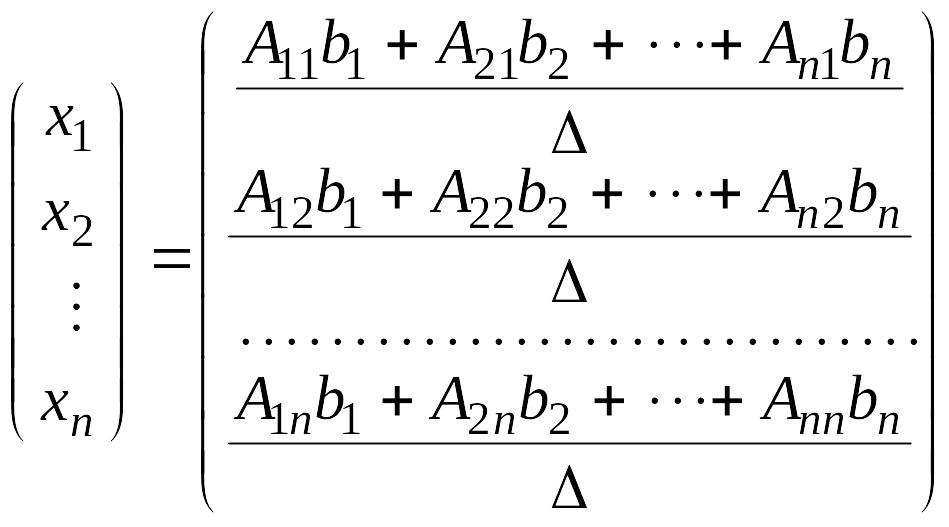Отсюда следует, что

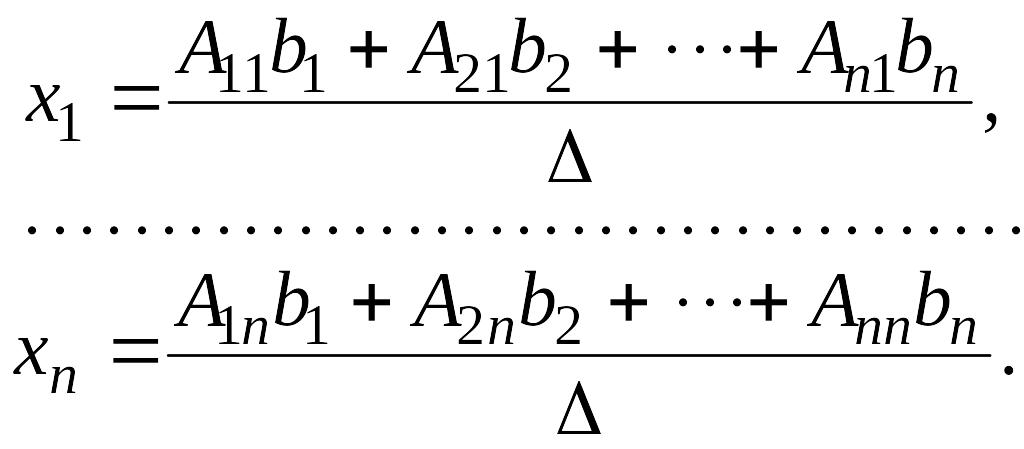
Но есть разложение определителя

по элементам первого столбца. Определитель получается из определителя путем замены первого столбца коэффициентов столбцом из свободных членов.

Итак, . Аналогично: где получен из путем замены второго столбца коэффициентов столбцом из свободных членов; ,…, .

Формулы

, (4.2)

называются формулами Крамера.

Итак, невырожденная система линейных уравнений с неиз­вестными имеет единственное решение, которое может быть найдено матричным способом (4.1) либо по формулам Крамера (4.2).

Пример 4.3. Решить систему

Решение.

, , .

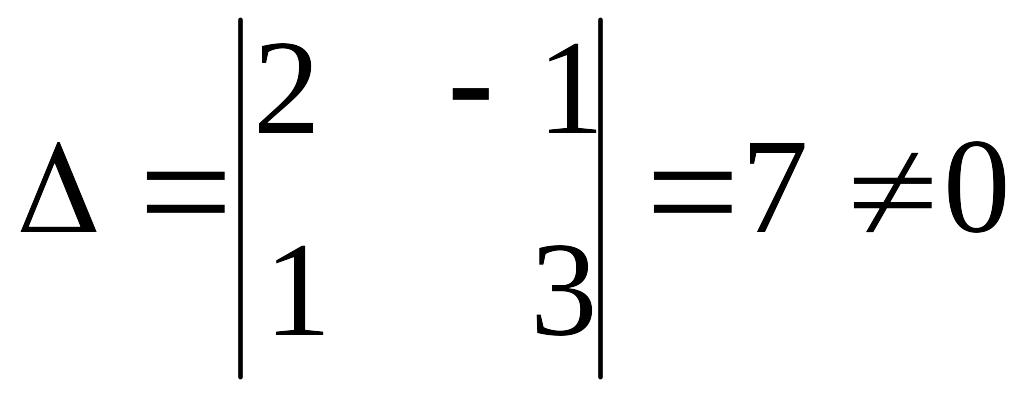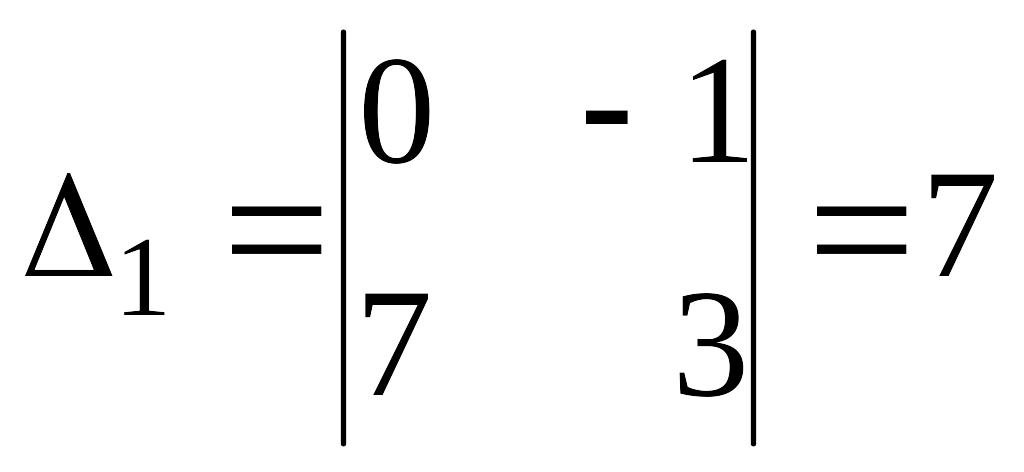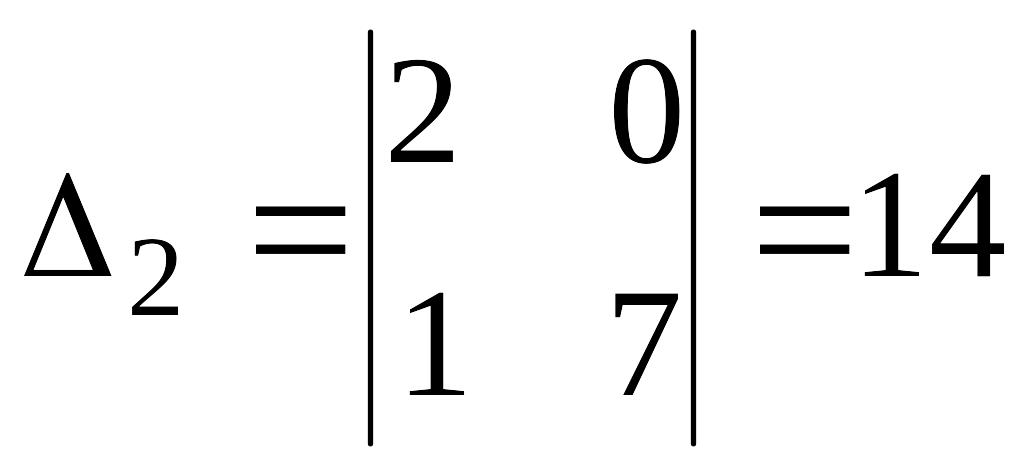Значит,

, .

4. Решение систем линейных уравнений методом Гаусса

Одним из наиболее универсальных и эффективных методов реше­ний линейных алгебраических систем является метод Гаусса, состоя­щий в последовательном исключении неизвестных.

Пусть дана система уравнений

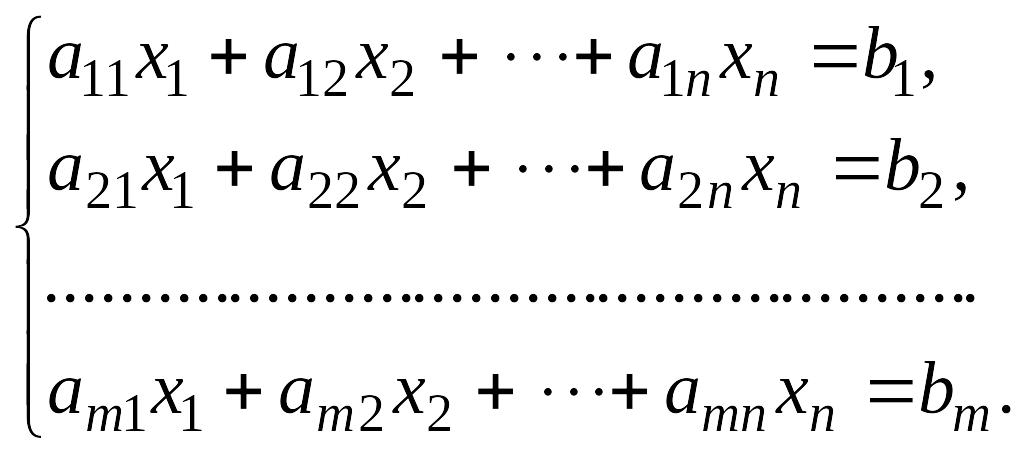
Процесс решения по методу Гаусса состоит из двух этапов. На пер­вом этапе (прямой ход) система приводится к ступенчатому (в част­ности, треугольному) виду.

Приведенная ниже система имеет ступенчатый вид

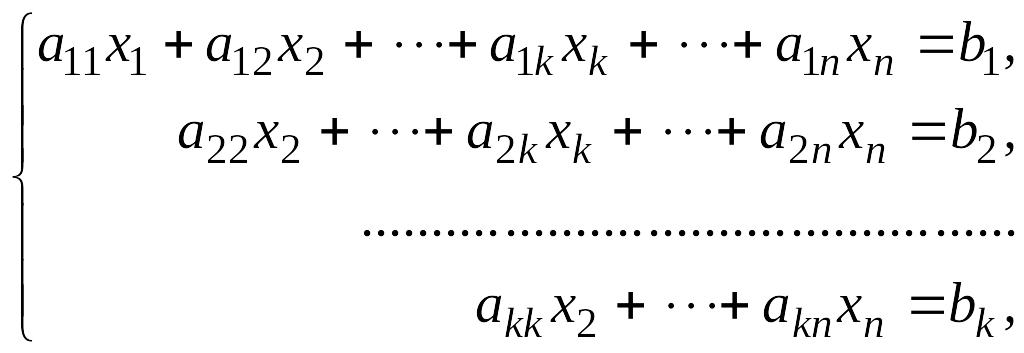
где , , . Коэффициенты называются главными элементами системы.

На втором этапе (обратный ход) идет последовательное определе­ние неизвестных из этой ступенчатой системы.

Опишем метод Гаусса подробнее.

Прямой ход.

Будем считать, что элемент (если , то первым в системе запишем уравнение, в котором коэффициент при отличен от нуля).

Преобразуем систему (4.3), исключив неизвестное во всех урав­нениях, кроме перового (используя элементарные преобразования си­стемы). Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему

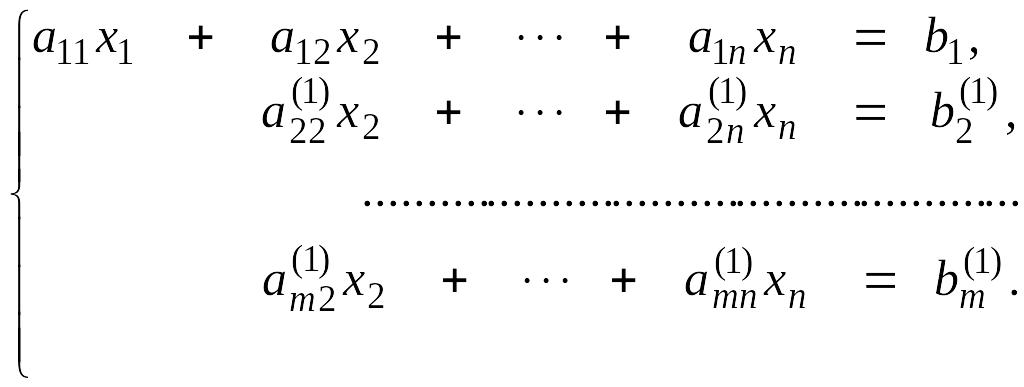
Здесь , ( ) — новые значения коэффициентов и правых частей, которые получаются после первого шага.

Аналогичным образом, считая главным элементом , ис­ключим неизвестное из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.

Если в процессе приведения системы (4.3) к ступенчатому виду по­явятся нулевые уравнения, т. е. равенства вида 0 = 0, их отбрасывают. Если же появится уравнение вида , a , то это свидетель­ствует о несовместности системы.

Обратный ход.

(Второй этап) заключается в решении ступенча­той системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой си­стемы выражаем первое неизвестное через остальные неизвестные ( ). Затем подставляем значение в предпоследнее урав­нение системы и выражаем через ( ); затем находим . Придавая свободным неизвестным ( ) произ­вольные значения, получим бесчисленное множество решений системы.

Замечание 1. Если ступенчатая система оказывается треуголь­ной, т. е. , то исходная система имеет единственное решение. Из последнего уравнения находим , из предпоследнего уравнения , далее поднимаясь по системе вверх, найдем все остальные неизвестные ( ).

Замечание 2. На практике удобнее работать не с системой (4.3), а с расши­ренной ее матрицей, выполняя все элементарные преобразования над ее строками.

Удобно, чтобы коэффициент был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на ).

Пример 4.4. Решить систему методом Гаусса:

Решение. В результате элементарных преобразований над расши­ренной матрицей системы

исходная система свелась к ступенчатой:

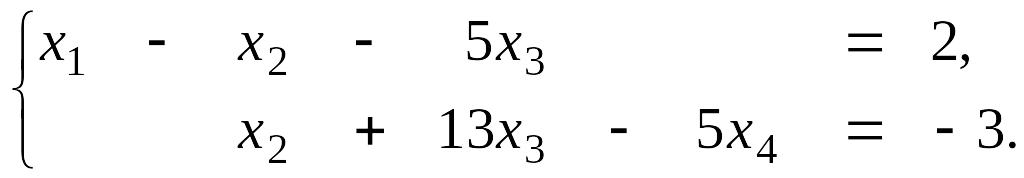
Поэтому общее решение системы: ; . Если положить, например, , , то найдем одно из частных решений этой системы , , , .

Пример 4.5. Решить систему методом Гаусса:

Решение. Произведем элементарные преобразования над строчками расширенной матрицы системы:

.

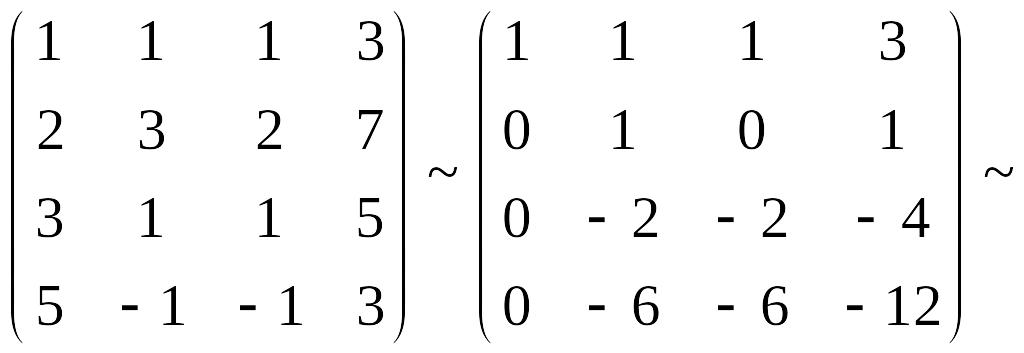
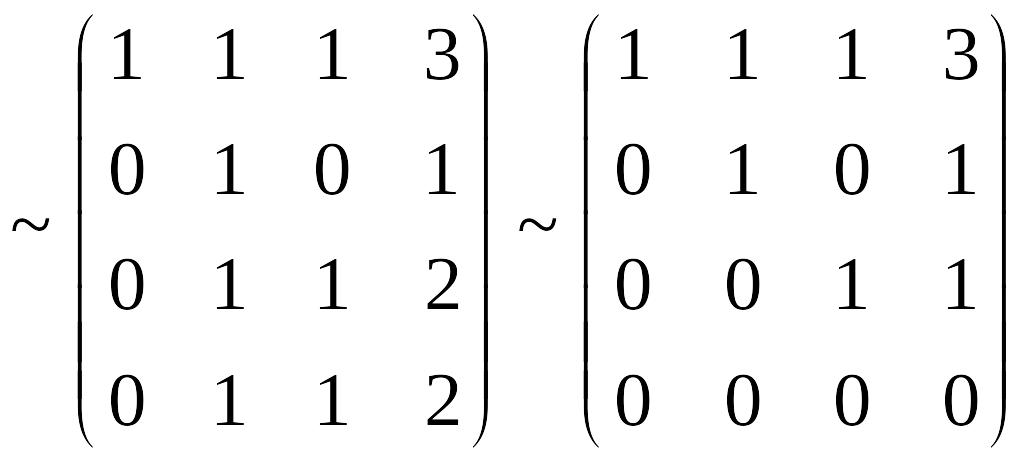Полученная матрица соответствует системе

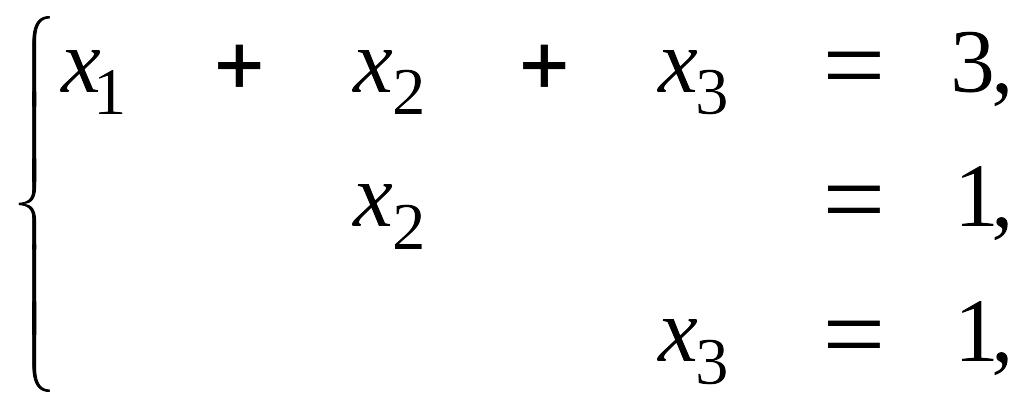
Осуществляя обратный ход, находим , , .