
- •Часть I
- •Часть I
- •Введение
- •I. Элементы линейной алгебры
- •§1. Матрицы
- •Основные понятия
- •Действия над матрицами
- •§2. Определители
- •Основные понятия
- •2.2. Свойства определителей
- •§3. Невырожденные матрицы
- •Основные понятия
- •Обратная матрица
- •3.3. Ранг матрицы
- •§4. Системы линейных уравнений
- •Основные понятия
- •Решение систем линейных уравнений. Теорема Кронекера-Капелли
- •Решение невырожденных линейных систем. Формулы Крамера
- •Решение систем линейных уравнений методом Гаусса
- •Системы линейных однородных уравнений
- •II. Элементы векторной алгебры
- •§5. Векторы
- •5.1. Основные понятия
- •5.2. Линейные операции над векторами
- •5.3. Проекция вектора на ось
- •5.4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
- •5.5. Действия над векторами, заданными проекциями
- •§6. Скалярное произведение векторов и его свойства
- •6.1. Определение скалярного произведения
- •6.2. Свойства скалярного произведения
- •6.3. Выражение скалярного произведения через координаты
- •6.4. Некоторые приложения скалярного произведения
- •§ 7. Векторное произведение векторов и его свойства
- •7.1. Определение векторного произведения
- •7.2. Свойства векторного произведения
- •7.3. Выражение векторного произведения через координаты
- •7.4. Некоторые приложения векторного произведения
- •§8. Смешанное произведение векторов
- •8.1. Определение смешанного произведения, его геометрический смысл
- •8.2. Свойства смешанного произведения
- •8.3. Выражение смешанного произведения через координаты
- •8.4. Некоторые приложения смешанного произведения
- •III. Аналитическая геометрия на плоскости
- •§9. Система координат на плоскости
- •9.1. Основные понятия
- •9.2. Основные приложения метода координат на плоскости
- •9.3. Преобразование системы координат
- •§10. Линии на плоскости
- •10.1. Основные понятия
- •10.2. Уравнения прямой на плоскости
- •10.3. Прямая линия на плоскости. Основные задачи
- •§11. Линии второго порядка на плоскости
- •11.1. Основные понятия
- •11.2. Окружность
- •11.3. Эллипс
- •11.4. Гипербола
- •IV. Аналитическая геометрия в пространстве
- •§12. Уравнения поверхности и линии в пространстве
- •12.1. Основные понятия
- •12.2. Уравнения плоскости в пространстве
- •12.3. Плоскость. Основные задачи
- •12.4. Уравнения прямой в пространстве
- •12.5. Прямая линия в пространстве. Основные задачи
- •12.6. Прямая и плоскость в пространстве. Основные задачи
- •12.7. Цилиндрические поверхности
- •12.8. Поверхности вращения. Конические поверхности
- •12.9. Канонические уравнения поверхностей второго порядка
- •V. Введение в анализ
- •§13. Множества. Действительные числа
- •13.1. Основные понятия
- •13.2. Числовые множества. Множество действительных чисел
- •13.3. Числовые промежутки. Окрестность точки
- •§14. Функции
- •14.1. Понятие функции
- •14.2. Числовые функции. График функции. Способы задания функций
- •14.3. Основные характеристики функции
- •14.4. Обратная функция
- •14.5. Сложная функция
- •14.6. Основные элементарные функции и их графики
- •§15. Последовательности
- •15.1. Числовая последовательность
- •15.2. Предел числовой последовательности
- •15.3. Предельный переход в неравенствах
- •15.4. Предел монотонной ограниченной последовательности. Число . Натуральные логарифмы
- •§16. Предел функции
- •16.1. Предел функции в точке
- •16.2. Односторонние пределы
- •16.3. Предел функции при
- •16.4. Бесконечно большая функция (б.Б.Ф.)
- •§17. Бесконечно малые функции (б.М.Ф.)
- •17.1. Определения и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •17.3. Основные теоремы о пределах
- •17.4. Признаки существования пределов
- •17.5. Первый замечательный предел
- •17.6. Второй замечательный предел
- •§18. Эквивалентные бесконечно малые функции
- •18.1. Сравнение бесконечно малых функций
- •18.2. Эквивалентные бесконечно малые и основные теоремы о них
- •18.3. Применение эквивалентных бесконечно малых функций
- •§ 19. Непрерывность функций
- •19.1. Непрерывность функции в точке
- •19.2. Непрерывность функции в интервале и на отрезке
- •19.3. Точки разрыва функции и их классификация
- •19.4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •19.5. Свойства функций, непрерывных на отрезке
- •Заключение
- •Библиографический список
- •Часть I
- •394026 Воронеж, Московский просп., 14
I. Элементы линейной алгебры
§1. Матрицы
Основные понятия
Определение.
Матрицей
называется
прямоугольная таблица чисел, содержащая
![]() строк одинаковой длины (или
строк одинаковой длины (или![]() столбцов одинаковой длины).
столбцов одинаковой длины).
Матрица записывается в виде
 ,
,
или,
сокращенно,
![]() ,
где
,
где
![]() (т. е.
(т. е.
![]() )
— номер
строки,
)
— номер
строки,
![]() (т. е.
(т. е.
![]() )
— номер столбца.
)
— номер столбца.
Матрицу
![]() называют матрицей размера
называют матрицей размера
![]() и пишут
и пишут
![]() .
Числа
.
Числа
![]() ,
составляющие
матрицу, называются ее
элементами.
Элементы
,
составляющие
матрицу, называются ее
элементами.
Элементы
![]() ,
…,
,
…,
![]() ,
стоящие на диагонали, идущей из левого
верхнего угла, образуют главную
диагональ.
,
стоящие на диагонали, идущей из левого
верхнего угла, образуют главную
диагональ.
Матрицы равны между собой, если равны все соответствующие элементы этих матриц,
т. е.
![]() ,
если
,
если
![]() ,
где
,
где
![]() ,
.
,
.
Матрица,
у которой число строк равно числу
столбцов, называется квадратной.
Квадратную
матрицу размера
![]() называют матрицей
называют матрицей
![]() -го
порядка.
-го
порядка.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная
матрица, у которой каждый элемент главной
диагонали равен единице, называется
единичной.
Обозначается
буквой
![]() .
.
Пример 1.1.
 — единичная
матрица 3-го порядка.
— единичная
матрица 3-го порядка.
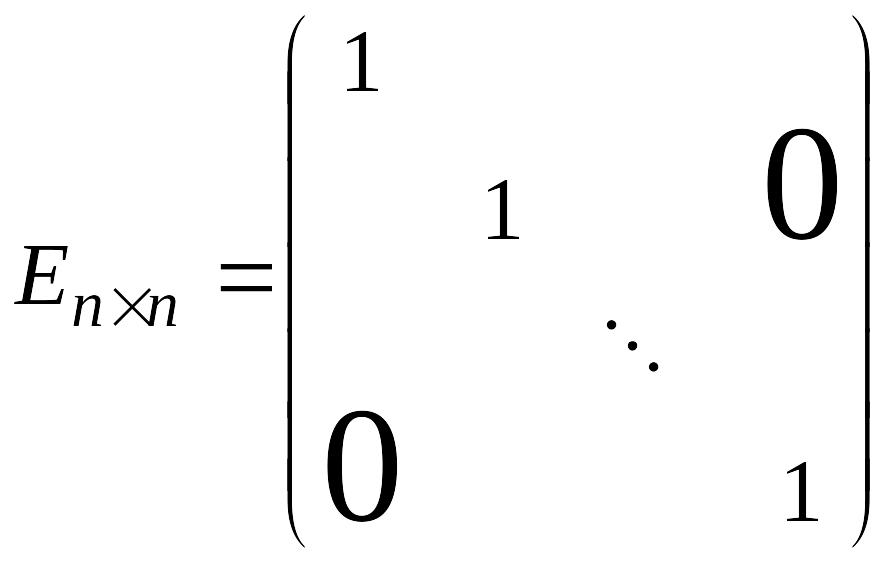 — единичная
матрица
-го
порядка.
— единичная
матрица
-го
порядка.
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Матрица,
все элементы которой равны нулю,
называется нулевой.
Обозначается
буквой
![]() .
Имеет вид
.
Имеет вид
 .
.
В
матричном исчислении матрицы
![]() и
и
![]() играют роль чисел 0 и 1 в арифметике.
играют роль чисел 0 и 1 в арифметике.
Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:
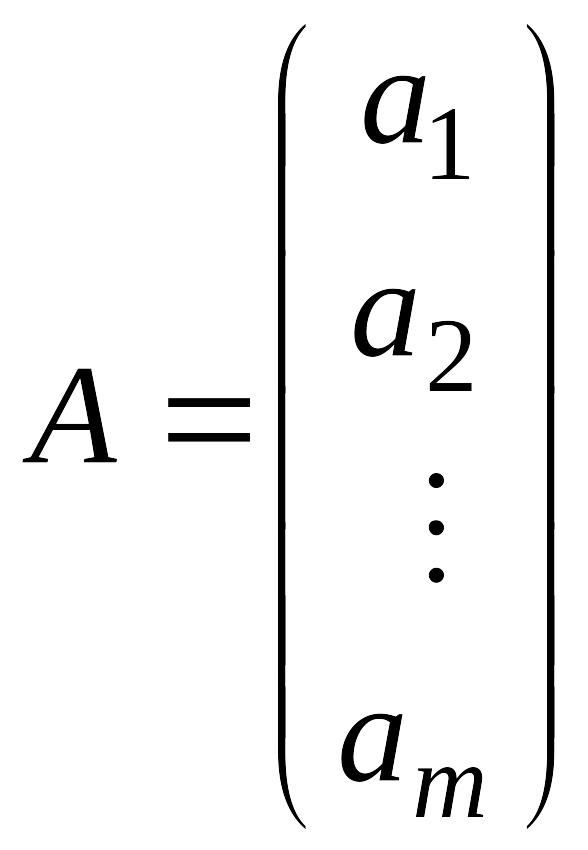 ,
,
![]() .
.
Матрица
размера
![]() ,
состоящая из одного числа, отождествляется
с этим числом, т. е.
,
состоящая из одного числа, отождествляется
с этим числом, т. е.
![]() есть 5.
есть 5.
Матрица,
полученная из данной заменой каждой ее
строки столбцом с тем же номером,
называется матрицей транспонированной
к данной.
Обозначается
![]() .
.
Так,
если
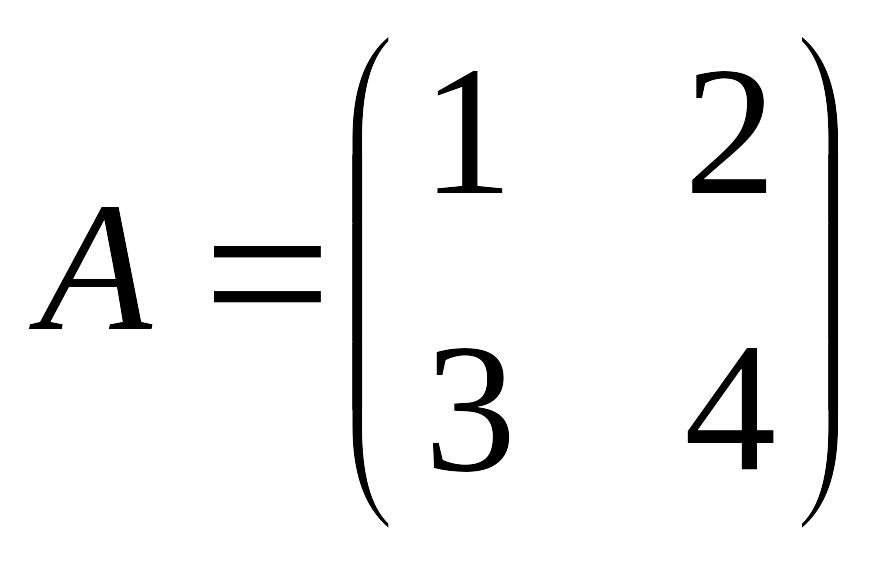 ,
то
,
то
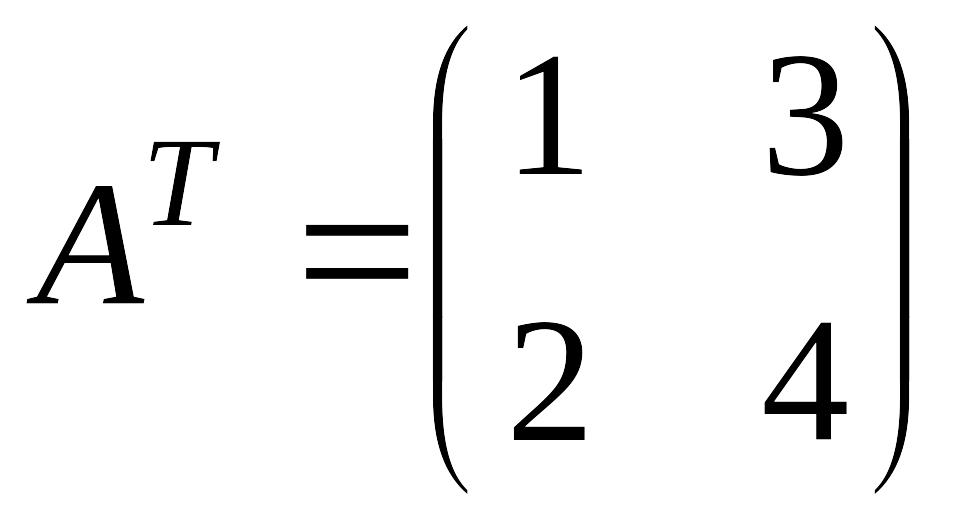 ,
если
,
если
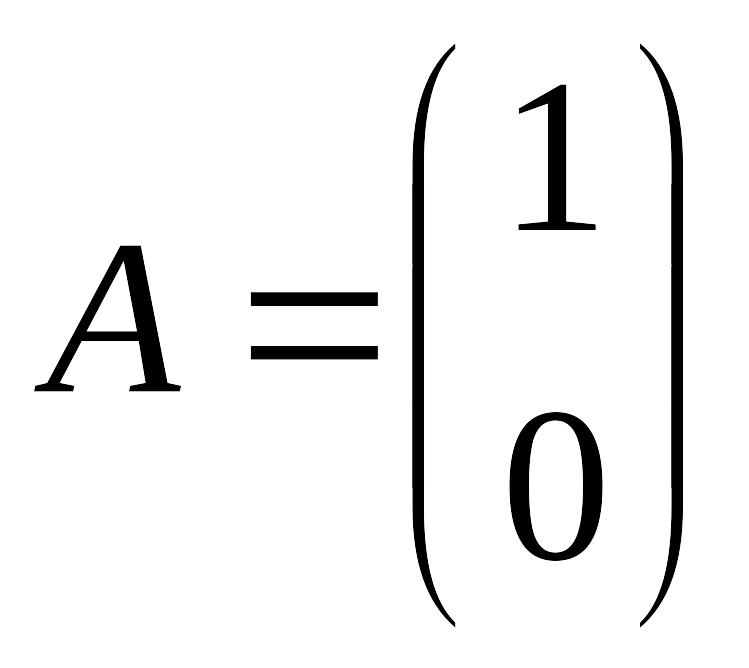 ,
то
,
то
![]() .
.
Транспонированная
матрица обладает следующим свойством:
![]() .
.
Действия над матрицами
Сложение.
Операция сложения матриц вводится только для матриц одинаковых размеров.
Определение.
Суммой двух матриц
![]() и
и
![]() называется
матрица
называется
матрица
![]() такая, что
такая, что
![]() (
,
).
(
,
).
Пример 1.2.
 .
.
Аналогично определяется разность матриц.
Умножение на число.
Определение.
Произведением матрицы
на число
![]() называется
матрица
такая, что
называется
матрица
такая, что
![]() ,
(
,
).
,
(
,
).
Пример 1.3.
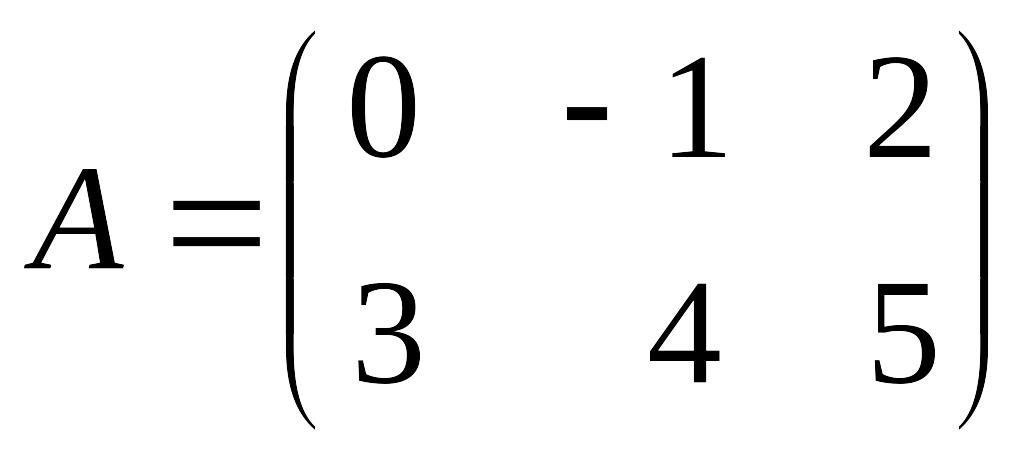 ,
,
![]() ,
,
 .
.
Матрица
![]() называется противоположной
матрице
называется противоположной
матрице
![]() .
.
Разность
матриц
![]() можно определить так:
можно определить так:
![]() .
.
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
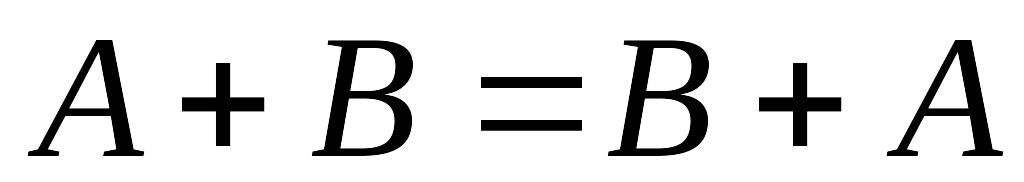 ;
;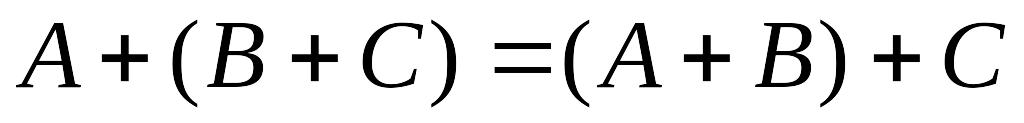 ;
;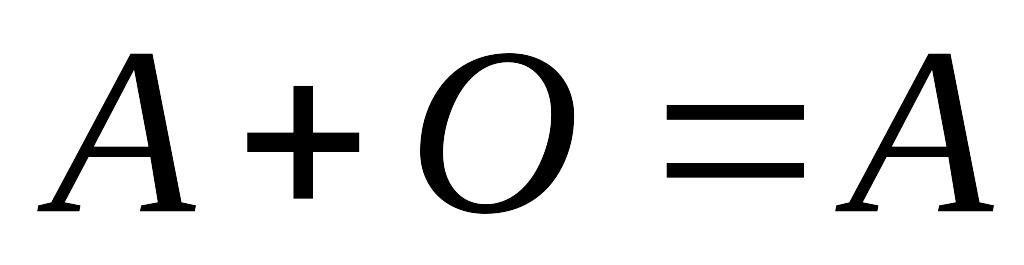 ;
; ;
;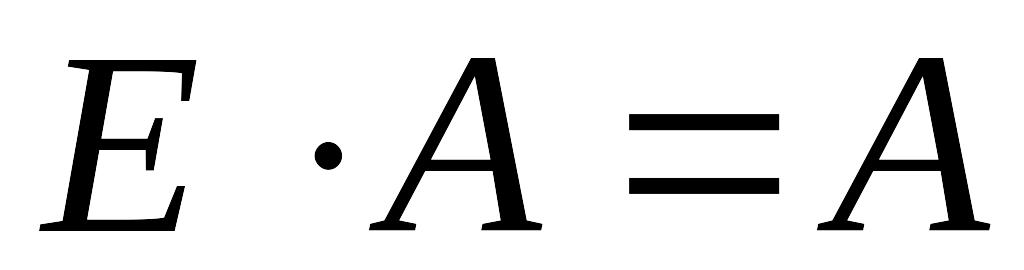 ;
;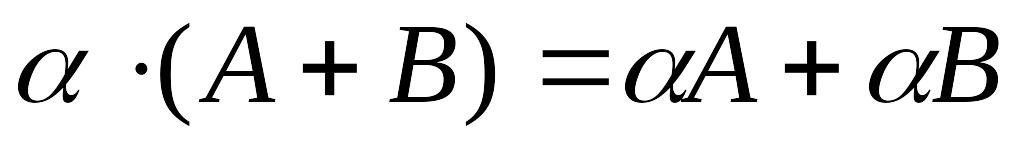 ;
; ,
,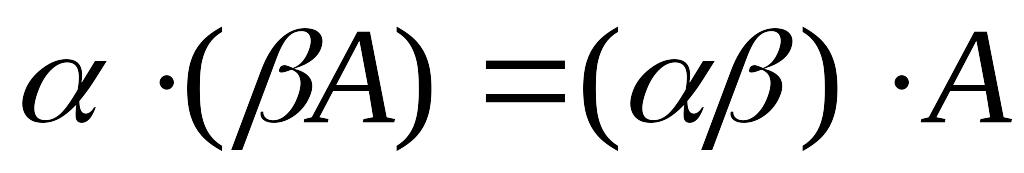 ,
,
где
,
![]() ,
,
![]() — матрицы,
— матрицы,
![]() и
и
![]() — числа.
— числа.
Элементарные преобразования матриц.
Элементарными преобразованиями матриц являются:
• перестановка местами двух параллельных рядов матрицы;
• умножение всех элементов ряда матрицы на число, отличное от нуля;
• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Две
матрицы
и
называются эквивалентными,
если одна
из них получается из другой с помощью
элементарных преобразований.
Записывается
![]() .
.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например
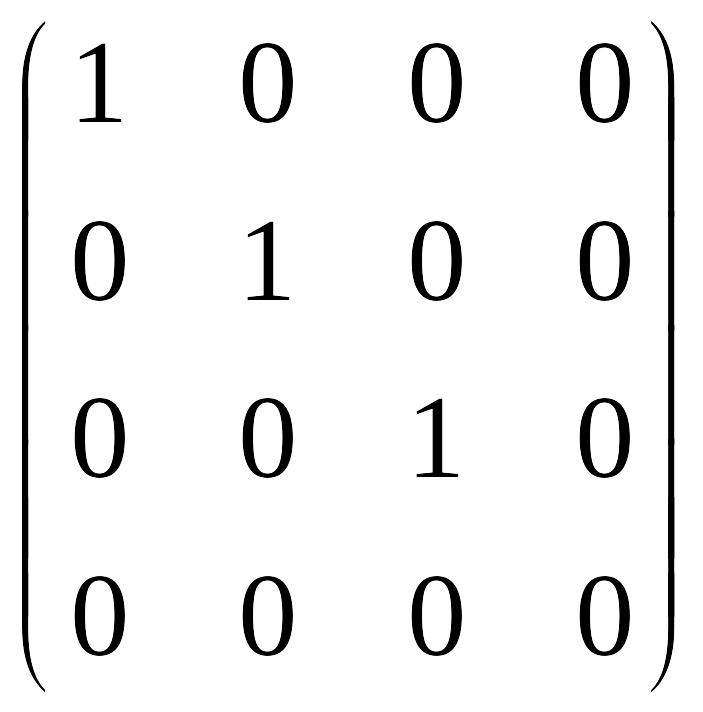 .
.
Пример 1.4. Привести к каноническому виду матрицу
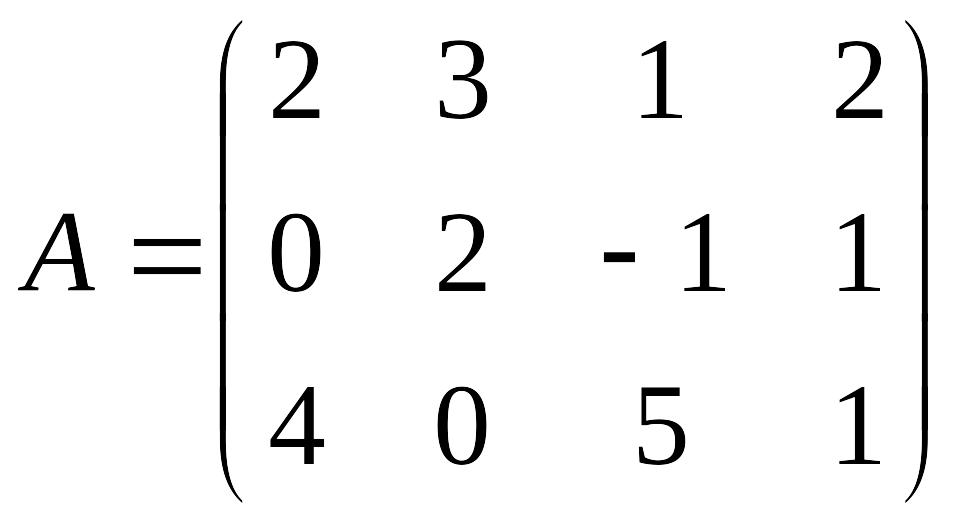 .
.
Решение. Выполняя элементарные преобразования, получаем
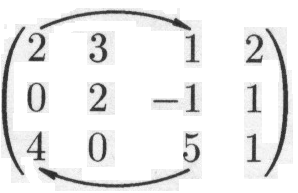
![]()
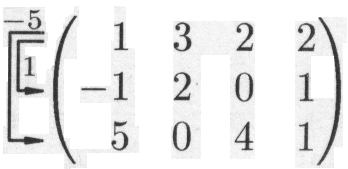
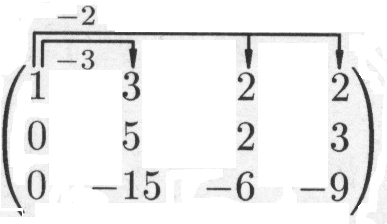
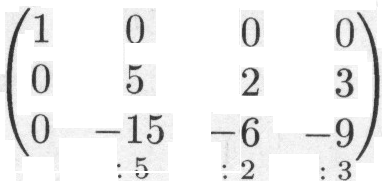
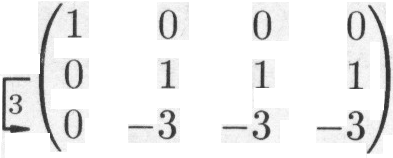
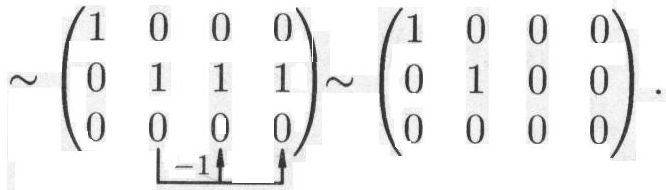
Произведение матриц.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Определение.
Произведением матрицы
![]() на матрицу
на матрицу
![]() называется матрица
называется матрица
![]() такая, что
такая, что
![]() ,
где
,
,
где
,
![]() ,
,
т.
е. элемент
![]() -й
строки и
-й
строки и
![]() -гo
столбца
матрицы произведения
равен сумме произведений элементов
-й
строки матрицы
на соответствующие элементы
-гo
столбца
матрицы
.
-гo
столбца
матрицы произведения
равен сумме произведений элементов
-й
строки матрицы
на соответствующие элементы
-гo
столбца
матрицы
.
Получение
элемента
![]() схематично изображается так:
схематично изображается так:
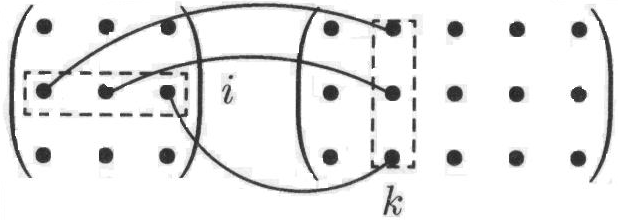
Если
матрицы
и
квадратные одного размера, то произведения
![]() и
и
![]() всегда существуют. Легко показать, что
всегда существуют. Легко показать, что
![]() ,
где
— квадратная матрица,
— единичная матрица того же размера.
,
где
— квадратная матрица,
— единичная матрица того же размера.
Пример 1.5.
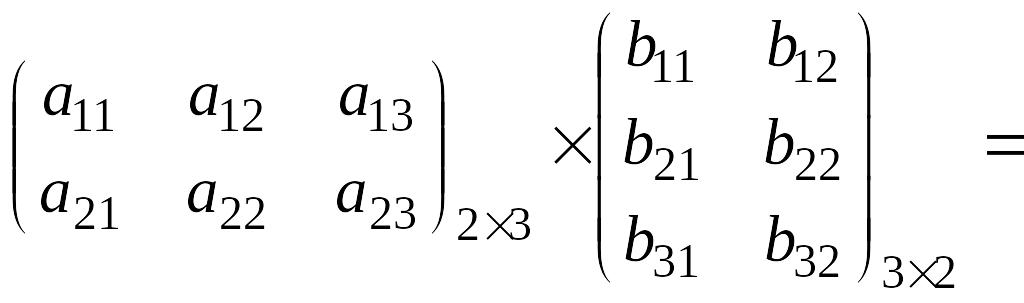
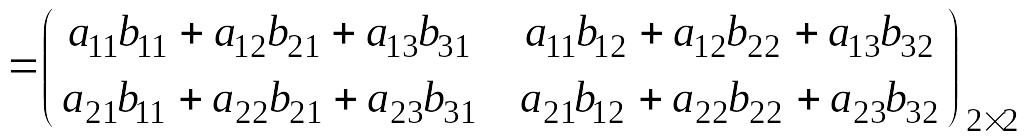 .
.
Пример 1.6.
 ,
,
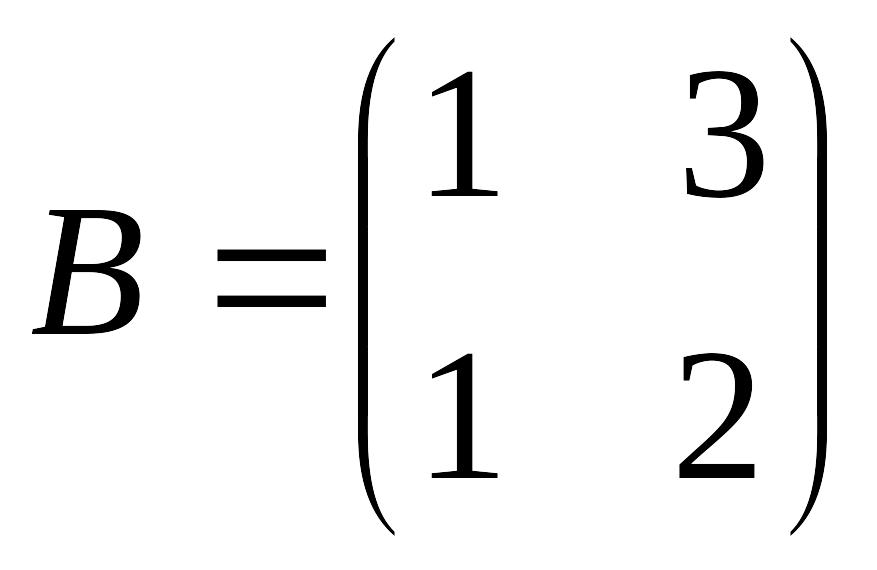 .
.
Тогда
произведение
![]() не определено,
так как число столбцов матрицы
(3) не совпадает с числом строк матрицы
(2). При этом
определено произведение
не определено,
так как число столбцов матрицы
(3) не совпадает с числом строк матрицы
(2). При этом
определено произведение
![]() ,
которое считают следующим образом:
,
которое считают следующим образом:
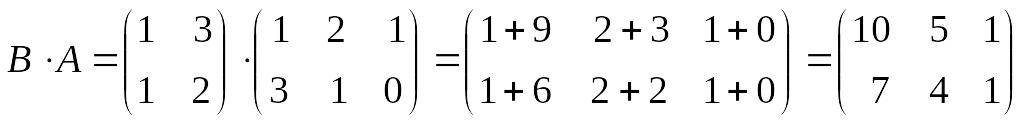
Матрицы
и
называются перестановочными,
если
![]() .
.
Умножение матриц обладает следующими свойствами:
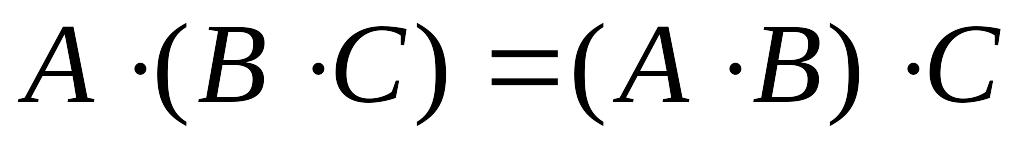 ;
;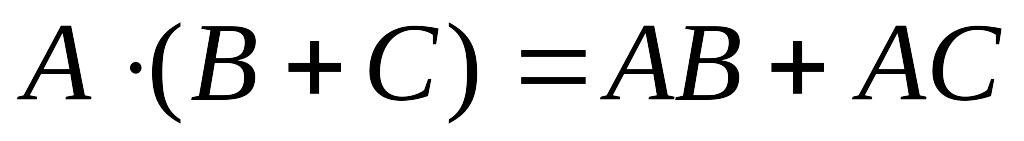 ;
;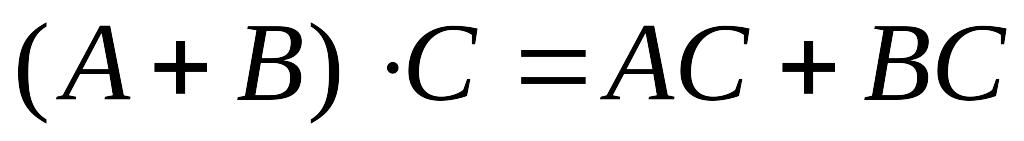 ;
;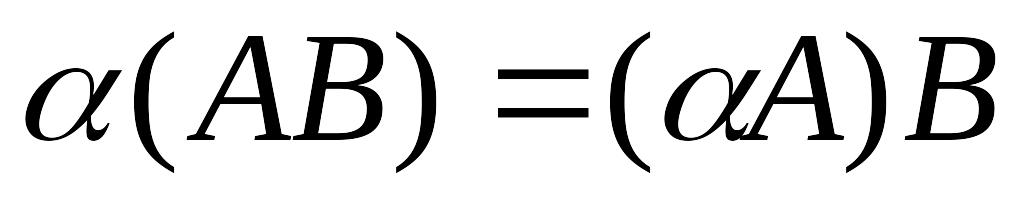 ,
,
если, конечно, написанные суммы и произведения матриц имеют смысл.
Для операции транспонирования верны свойства:
 ;
;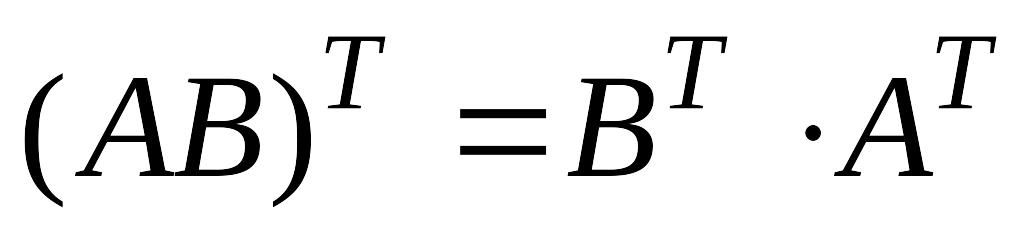 .
.
