§17. Бесконечно малые функции (б.М.Ф.)

17.1. Определения и основные теоремы

Определение. Функция называется бесконечно малой при , если

. (17.1)

По определению предела функции равенство (17.1) означает: для лю­бого числа найдется число такое, что для всех , удо­влетворяющих неравенству , выполняется неравенство .

Аналогично определяется б.м.ф. при , , , : во всех этих случаях .

Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами , и т. д.

Примерами б.м.ф. служат функции при ; при ; при , .

Другой пример: , , — бесконечно малая последовательность.

Теорема 17.1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

Доказательство. Пусть и — две б.м. функции при . Это значит, что , т.е. для любого , а значит, и найдется число такое, что для всех , удовлетворяющих неравенству , выполняется неравенство

(17.2)

и , т. е.

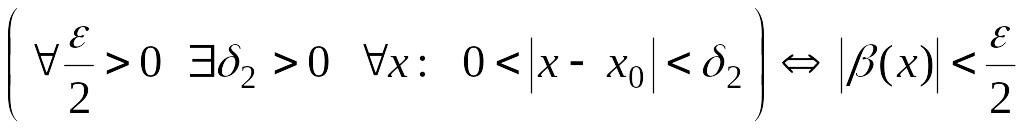. (17.3)

Пусть — наименьшее из чисел и . Тогда для всех , удовлетворяющих неравенству , выполняются оба неравен­ства (17.2) и (17.3). Следовательно, имеет место соотношение

.

Таким образом,

.

Это значит, что , т. е. — б.м.ф. при .

Аналогично проводится доказательство для любого конечного чи­сла б.м. функций.

Теорема 17.2. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.

Доказательство. Пусть функция ограничена при . Тогда существует такое число , что

(17.4)

для всех из -окрестности точки . И пусть — б.м.ф. при . Тогда для любого , а значит, найдется та­кое число , что при всех , удовлетворяющих неравенству , выполняется неравенство

. (17.5)

Обозначим через наименьшее из чисел и . Тогда для всех , удовлетворяющих неравенству , выполняются оба неравенства (17.4) и (17.5). Следовательно, . А это означает, что произведение при есть бесконечно малая функция.

Следствие 17.1. Так как всякая б.м.ф. ограничена, то из теоремы (17.2) вытекает: произведение двух б.м.ф. есть функция бесконечно малая.

Следствие 17.2. Произведение б.м.ф. на число есть функция беско­нечно малая.

Теорема 17.3. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция беско­нечно малая.

Доказательство. Пусть , a . Функция может быть представлена в виде произведения б.м.ф. на ограниченную функ­цию . Но тогда из теоремы (17.2) вытекает, что частное есть функция бесконечно малая.

Покажем, что функция ограниченная. Возьмем . То­гда, на основании определения предела, найдется , что для всех , удовлетворяющих неравенству выполняется нера­венство . А так как ,

то , т.е. . Следовательно,

,

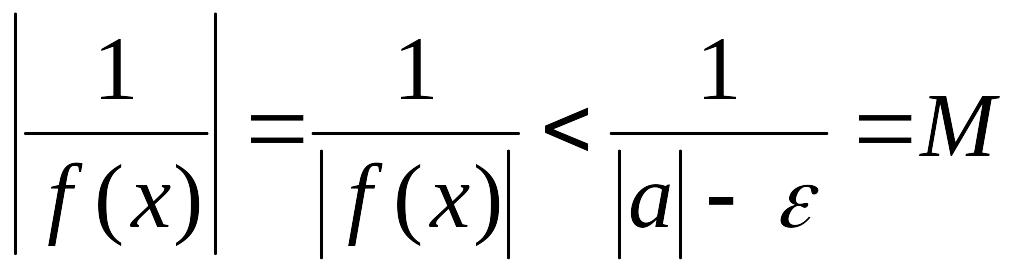т.е. функция — ограниченная.

Теорема 17.4. Если функция — бесконечно малая ( ), то функция есть бесконечно большая функция и наоборот: если функция — бесконечно большая, то — бесконечно малая.

Доказательство. Пусть есть б.м.ф. при , т.е. . Тогда

,

т.е. 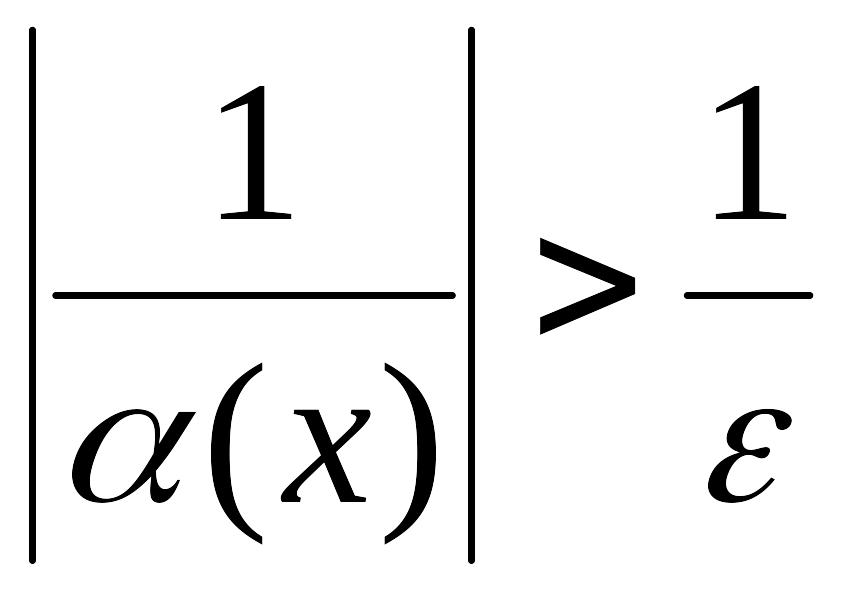, т.е. , где это означает, что функция есть бесконечно большая. Аналогично доказывается обратное утверждение.

Замечание. Доказательства теорем приводились для случая, когда , но они справедливы и для случая, когда .

Пример 17.1. Показать, что функция

при является бесконечно малой.

Решение. Так как , то функция есть бесконечно малая при . Функция , ограничена 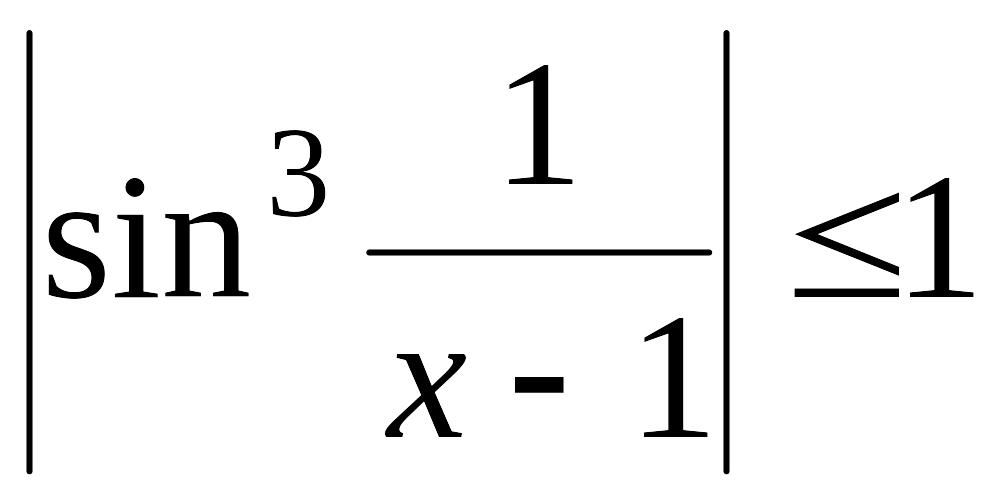. Функция представляет собой произведе­ние ограниченной функции на бесконечно малую . Значит, — бесконечно малая при .