
- •Часть I
- •Часть I
- •Введение
- •I. Элементы линейной алгебры
- •§1. Матрицы
- •Основные понятия
- •Действия над матрицами
- •§2. Определители
- •Основные понятия
- •2.2. Свойства определителей
- •§3. Невырожденные матрицы
- •Основные понятия
- •Обратная матрица
- •3.3. Ранг матрицы
- •§4. Системы линейных уравнений
- •Основные понятия
- •Решение систем линейных уравнений. Теорема Кронекера-Капелли
- •Решение невырожденных линейных систем. Формулы Крамера
- •Решение систем линейных уравнений методом Гаусса
- •Системы линейных однородных уравнений
- •II. Элементы векторной алгебры
- •§5. Векторы
- •5.1. Основные понятия
- •5.2. Линейные операции над векторами
- •5.3. Проекция вектора на ось
- •5.4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
- •5.5. Действия над векторами, заданными проекциями
- •§6. Скалярное произведение векторов и его свойства
- •6.1. Определение скалярного произведения
- •6.2. Свойства скалярного произведения
- •6.3. Выражение скалярного произведения через координаты
- •6.4. Некоторые приложения скалярного произведения
- •§ 7. Векторное произведение векторов и его свойства
- •7.1. Определение векторного произведения
- •7.2. Свойства векторного произведения
- •7.3. Выражение векторного произведения через координаты
- •7.4. Некоторые приложения векторного произведения
- •§8. Смешанное произведение векторов
- •8.1. Определение смешанного произведения, его геометрический смысл
- •8.2. Свойства смешанного произведения
- •8.3. Выражение смешанного произведения через координаты
- •8.4. Некоторые приложения смешанного произведения
- •III. Аналитическая геометрия на плоскости
- •§9. Система координат на плоскости
- •9.1. Основные понятия
- •9.2. Основные приложения метода координат на плоскости
- •9.3. Преобразование системы координат
- •§10. Линии на плоскости
- •10.1. Основные понятия
- •10.2. Уравнения прямой на плоскости
- •10.3. Прямая линия на плоскости. Основные задачи
- •§11. Линии второго порядка на плоскости
- •11.1. Основные понятия
- •11.2. Окружность
- •11.3. Эллипс
- •11.4. Гипербола
- •IV. Аналитическая геометрия в пространстве
- •§12. Уравнения поверхности и линии в пространстве
- •12.1. Основные понятия
- •12.2. Уравнения плоскости в пространстве
- •12.3. Плоскость. Основные задачи
- •12.4. Уравнения прямой в пространстве
- •12.5. Прямая линия в пространстве. Основные задачи
- •12.6. Прямая и плоскость в пространстве. Основные задачи
- •12.7. Цилиндрические поверхности
- •12.8. Поверхности вращения. Конические поверхности
- •12.9. Канонические уравнения поверхностей второго порядка
- •V. Введение в анализ
- •§13. Множества. Действительные числа
- •13.1. Основные понятия
- •13.2. Числовые множества. Множество действительных чисел
- •13.3. Числовые промежутки. Окрестность точки
- •§14. Функции
- •14.1. Понятие функции
- •14.2. Числовые функции. График функции. Способы задания функций
- •14.3. Основные характеристики функции
- •14.4. Обратная функция
- •14.5. Сложная функция
- •14.6. Основные элементарные функции и их графики
- •§15. Последовательности
- •15.1. Числовая последовательность
- •15.2. Предел числовой последовательности
- •15.3. Предельный переход в неравенствах
- •15.4. Предел монотонной ограниченной последовательности. Число . Натуральные логарифмы
- •§16. Предел функции
- •16.1. Предел функции в точке
- •16.2. Односторонние пределы
- •16.3. Предел функции при
- •16.4. Бесконечно большая функция (б.Б.Ф.)
- •§17. Бесконечно малые функции (б.М.Ф.)
- •17.1. Определения и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •17.3. Основные теоремы о пределах
- •17.4. Признаки существования пределов
- •17.5. Первый замечательный предел
- •17.6. Второй замечательный предел
- •§18. Эквивалентные бесконечно малые функции
- •18.1. Сравнение бесконечно малых функций
- •18.2. Эквивалентные бесконечно малые и основные теоремы о них
- •18.3. Применение эквивалентных бесконечно малых функций
- •§ 19. Непрерывность функций
- •19.1. Непрерывность функции в точке
- •19.2. Непрерывность функции в интервале и на отрезке
- •19.3. Точки разрыва функции и их классификация
- •19.4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •19.5. Свойства функций, непрерывных на отрезке
- •Заключение
- •Библиографический список
- •Часть I
- •394026 Воронеж, Московский просп., 14
9.2. Основные приложения метода координат на плоскости
Расстояние между двумя точками.
Требуется
найти расстояние
![]() между точками
между точками
![]() и
и
![]() плоскости
.
плоскости
.
Искомое
расстояние
равно длине вектора
![]() ,
т. е.
,
т. е.
![]() .
.
Деление отрезка в данном отношении.
Требуется
разделить отрезок
![]() ,
соединяющий точки
и
в заданном отношении
,
соединяющий точки
и
в заданном отношении
![]() ,
т. е. найти координаты точки
,
т. е. найти координаты точки
![]() отрезка
такой, что
отрезка
такой, что
![]() (см.
рис. 9.4).
(см.
рис. 9.4).
Введем
в рассмотрение векторы
![]() и
и
![]() .
Точка
делит отрезок
в отношении
,
если
.
Точка
делит отрезок
в отношении
,
если
![]() .
(9.1)
.
(9.1)
Но
![]() ,
т.е.
,
т.е.
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
Уравнение (9.1) принимает вид
.
Уравнение (9.1) принимает вид
![]() .
.
Учитывая, что равные векторы имеют равные координаты, получаем
![]() ,
т.е.
,
т.е.
![]() (9.2)
(9.2)
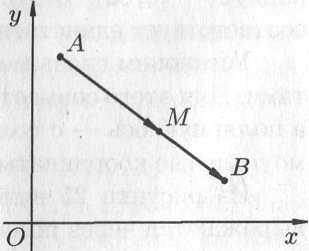
Рис. 9.4
и
![]() ,
т.е.
,
т.е.
![]() .
(9.3)
.
(9.3)
Формулы (9.2) и (9.3) называются формулами деления отрезка в данном отношении.
В
частности, при
![]() ,
т. е. если
,
т. е. если
![]() ,
то они примут вид
,
то они примут вид
![]() ,
,
![]() .
В этом случае точка
является серединой отрезка АВ.
.
В этом случае точка
является серединой отрезка АВ.
Замечание.
Если
![]() ,
то это означает, что точки
и
совпадают, если
,
то это означает, что точки
и
совпадают, если
![]() ,
то точка
лежит вне отрезка
— говорят, что точка
делит отрезок
внешним образом (
,
то точка
лежит вне отрезка
— говорят, что точка
делит отрезок
внешним образом (![]() ,
т.к. в противном случае
,
т.к. в противном случае
![]() ,
т.е.
,
т.е.
![]() ,
т. е.
,
т. е.
![]() ).
).
Площадь треугольника.
Требуется
найти площадь треугольника
![]() с вершинами
,
,
с вершинами
,
,
![]() .
.
Опустим
из вершин
,
![]() ,
,
![]() перпендикуляры
перпендикуляры
![]() ,
,
![]() ,
,
![]() на ось
(см. рис. 9.5).
на ось
(см. рис. 9.5).

Рис. 9.5
Очевидно, что
![]() .
.
Поэтому
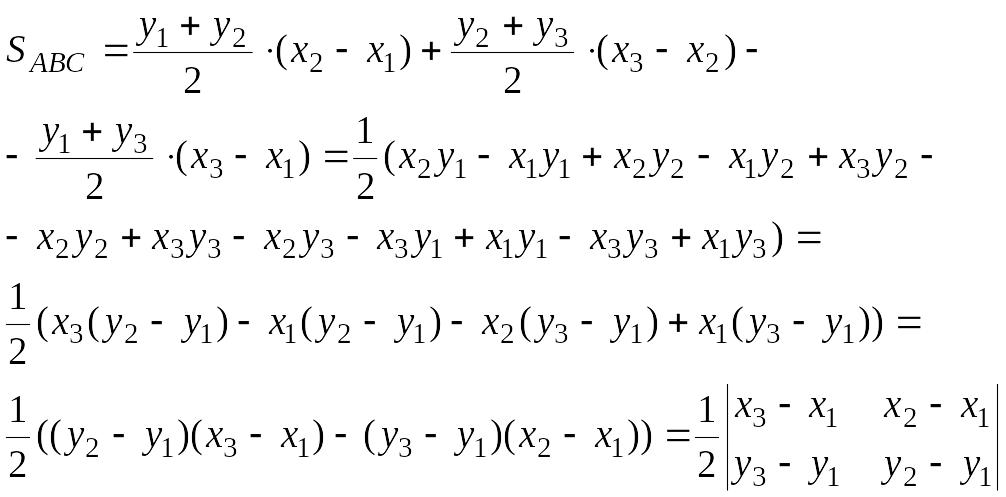
т. е.
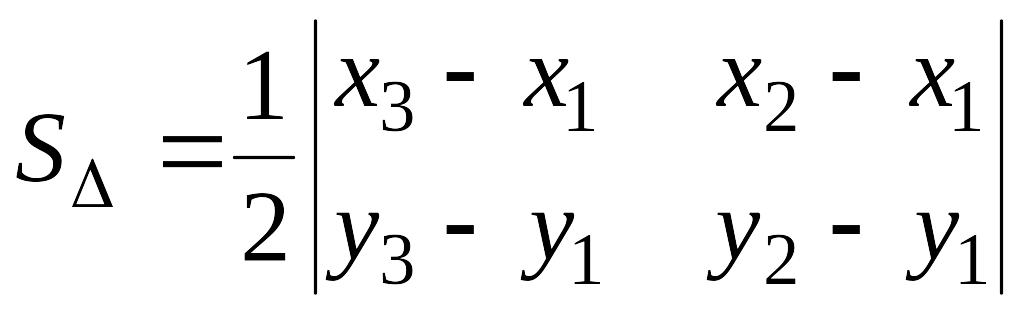 ,
,
Замечание.
Если при
вычислении площади треугольника получим
![]() ,
то это означает, что точки
,
,
лежат на одной прямой, если же получим
отрицательное число, то следует взять
его модуль.
,
то это означает, что точки
,
,
лежат на одной прямой, если же получим
отрицательное число, то следует взять
его модуль.
9.3. Преобразование системы координат
Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.
Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами произвольной точки плоскости в разных системах координат.
Параллельный перенос осей координат.
Пусть
на плоскости задана прямоугольная
система координат
.
Под параллельным переносом осей координат
понимают переход от системы координат
к новой системе
![]() ,
при котором меняется положение начала
координат, а направление осей и масштаб
остаются неизменными.
,
при котором меняется положение начала
координат, а направление осей и масштаб
остаются неизменными.
Пусть
начало новой системы координат точка
![]() имеет координаты
имеет координаты
![]() старой системе координат
,
т. е.
старой системе координат
,
т. е.
![]() .
Обозначим координаты произвольной
точки
плоскости в системе
через
.
Обозначим координаты произвольной
точки
плоскости в системе
через
![]() ,
а в новой системе
через
,
а в новой системе
через
![]() (см. рис. 9.6).
(см. рис. 9.6).
Рассмотрим векторы
![]() ,
,
![]() ,
,
![]() .
.
Так
как
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() .
.
Следовательно,

Полученные
формулы позволяют находить старые
координаты
и
по известным
новым
![]() и
и
![]() и наоборот.
и наоборот.
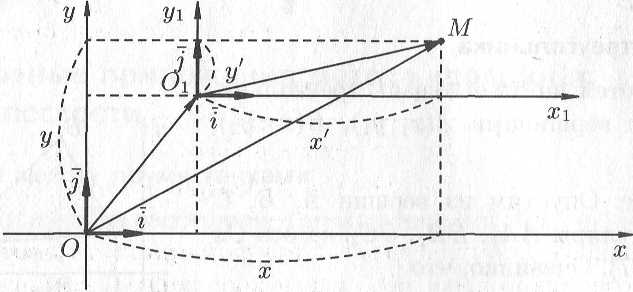
Рис. 9.6
Поворот осей координат.
Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.
Пусть новая система получена поворотом системы на угол .
Пусть — произвольная точка плоскости, — ее координаты в старой системе и — в новой системе.
Введем
две полярные системы координат с общим
полюсом
и полярными осями
и
![]() (масштаб одинаков). Полярный радиус
в обеих системах одинаков, а полярные
углы соответственно равны
(масштаб одинаков). Полярный радиус
в обеих системах одинаков, а полярные
углы соответственно равны
![]() и
,
где
— полярный угол в новой полярной системе.
и
,
где
— полярный угол в новой полярной системе.
По формулам перехода от полярных координат к прямоугольным имеем
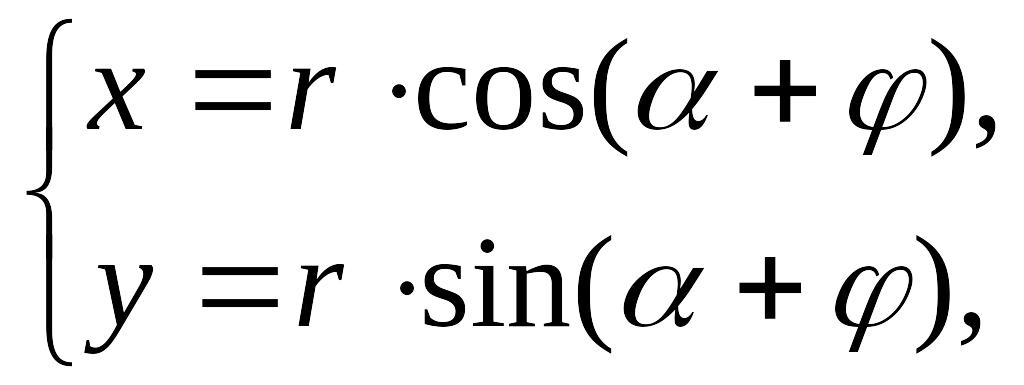 т.е.
т.е. 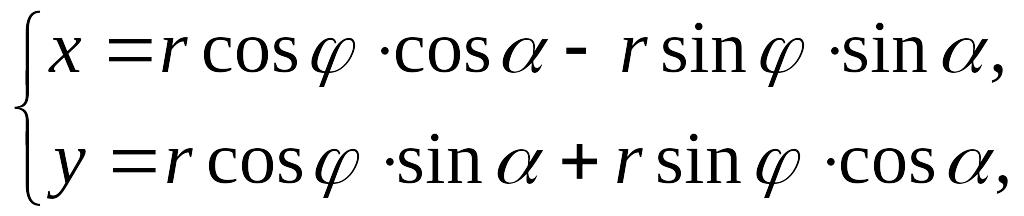
Ho
![]() и
и
![]() .
Поэтому
.
Поэтому .
.
Полученные формулы называются формулами поворота осей. Они позволяют определять старые координаты произвольной точки через новые координаты этой же точки , и наоборот.
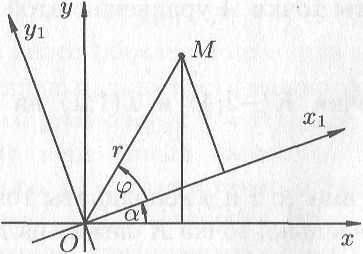
Рис. 9.7
Если
новая система координат
получена из старой
путем параллельного переноса осей
координат и последующим поворотом осей
на угол
(см. рис. 9.8), то путем введения вспомогательной
системы
![]() легко получить формулы
легко получить формулы
 ,
,
выражающие
старые координаты
и
произвольной точки через ее новые
координаты
![]() и
и
![]() .
.
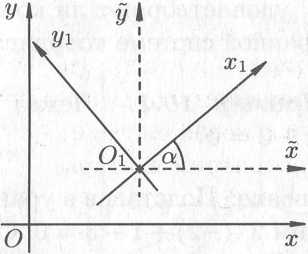
Рис. 9.8
