5. Системы линейных однородных уравнений

Пусть дана система линейных однородных уравнений

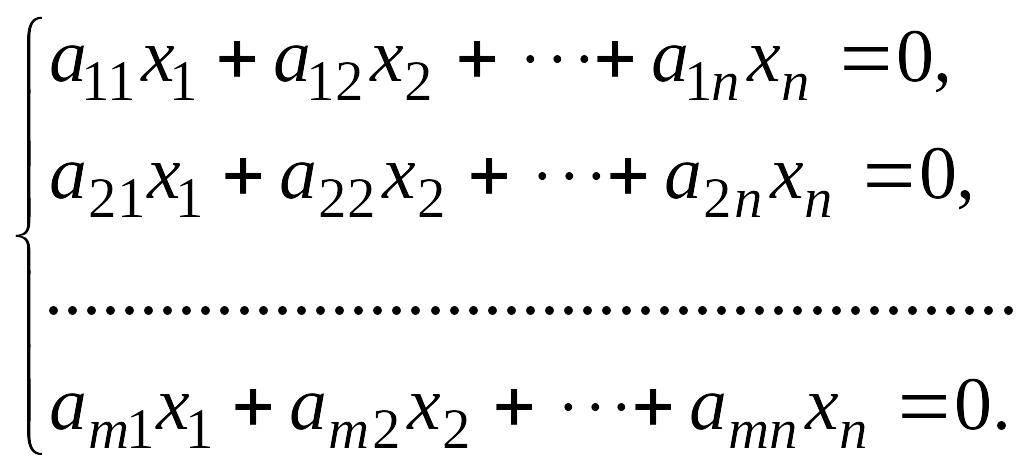
Очевидно, что однородная система всегда совместна ( ), она имеет нулевое (тривиальное) решение .

Рассмотрим при каких условиях однородная система имеет и ненулевые решения.

Теорема 4.4. Для того чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных, т. е. .

Доказательство.

Необходимость. Так как ранг не может превосходить размера матрицы, то, очевид­но, . Пусть . Тогда один из миноров размера отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение. , , . Значит, других, кро­ме тривиальных, решений нет. Итак, если есть нетривиальное решение, то .

Достаточность. Пусть . Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения.

Пусть дана однородная система линейных уравнений с неизвестными

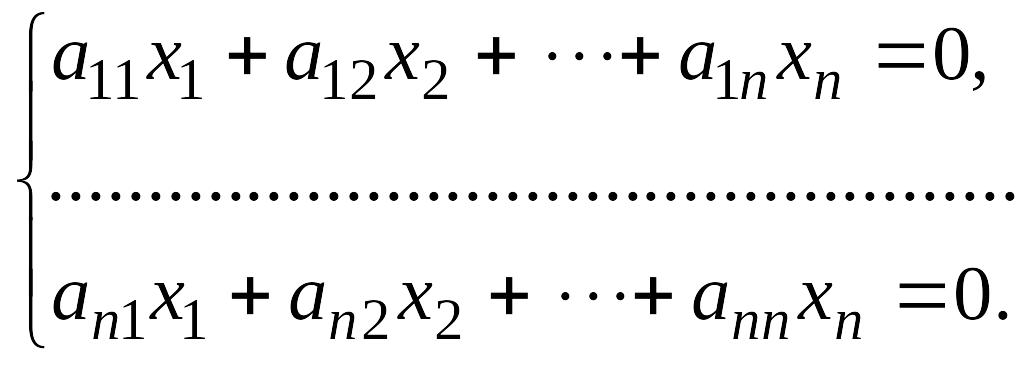
Теорема 4.5. Для того, чтобы однородная система линейных урав­нений с неизвестными имела ненулевые решения, необходимо и до­статочно, чтобы ее определитель был равен нулю, т. е. .

Если система имеет ненулевые решения, то . Ибо при система имеет только единственное, нулевое решение. Если же , то ранг основной матрицы системы меньше числа неизвестных, т. е. . И, значит, система имеет бесконечное множество (ненулевых) решений.

Пример 4.6. Решить систему

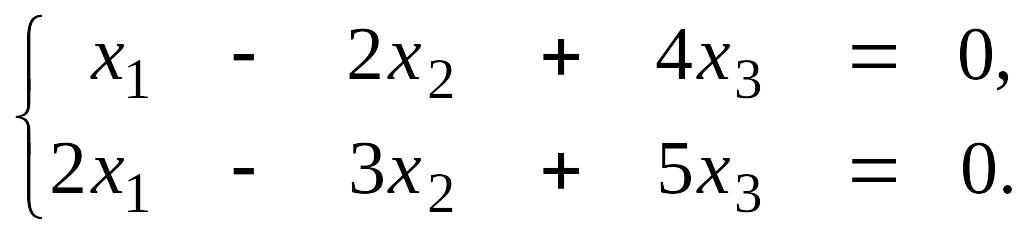
Решение.

, , .

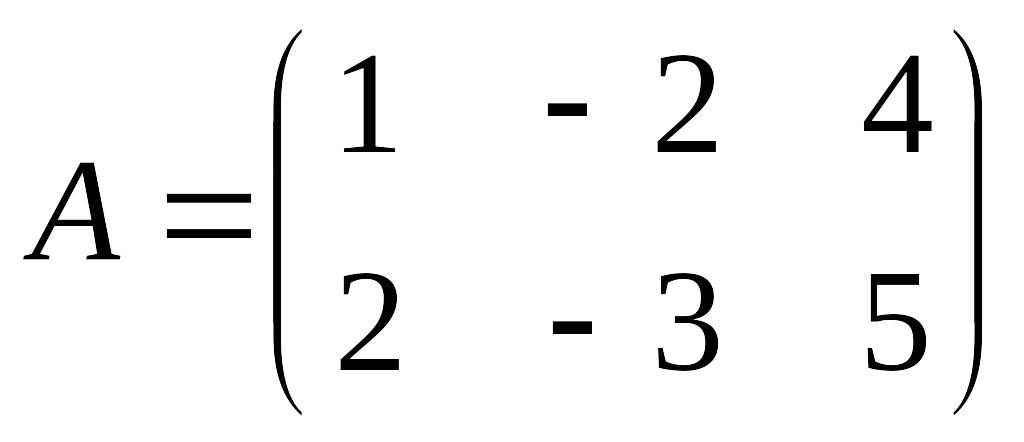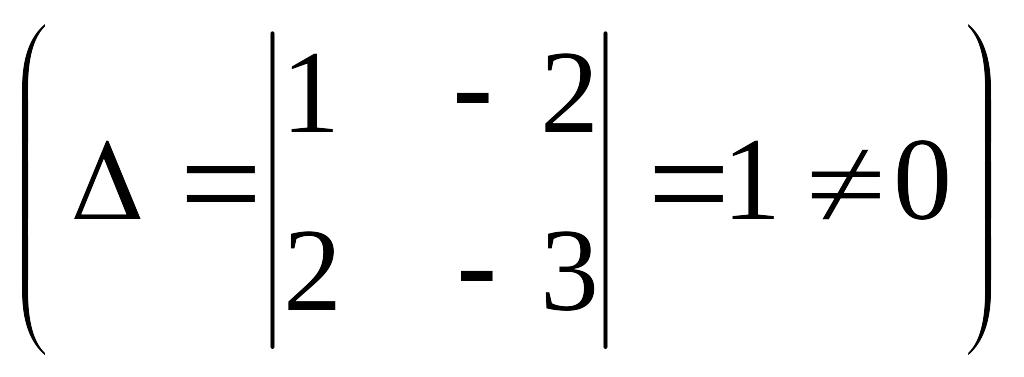Так как , то система имеет бесчисленное множество решений. Найдем их

, .

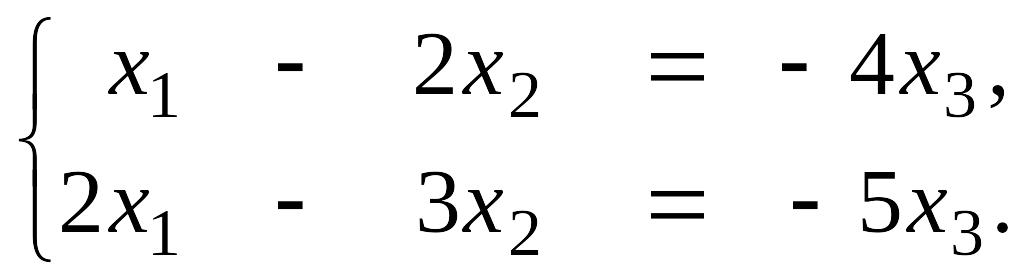
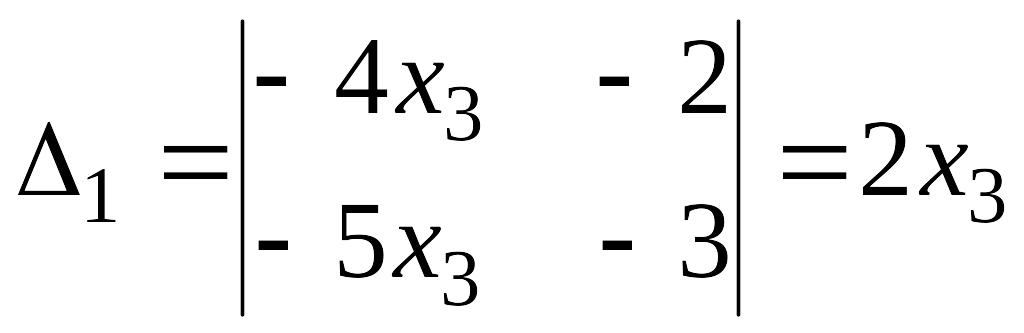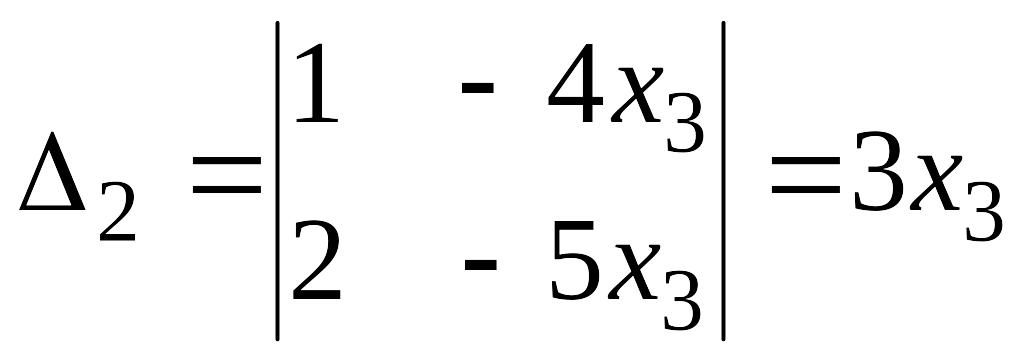Стало быть, , — общее решение.

Положив , получаем одно частное решение. , , . Положив , получаем второе частное решение. , , и т. д.

II. Элементы векторной алгебры

§5. Векторы

5.1. Основные понятия

Определение. Величины, которые полностью определяются своим численным значением, называются скалярными.

Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.

Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.

Определение. Вектор — это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление.

Если — начало вектора, а — его конец, то вектор обозначается символом или . Вектор (у него начало в точке , а конец в точке ) называется противоположным вектору . Вектор, про­тивоположный вектору , обозначается .

Длиной или модулем вектора называется длина отрезка и обозначается . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается . Нулевой вектор направления не имеет.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через . Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается .

Определение. Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают .

Коллинеарные векторы могут быть направлены одинаково или противоположно.

Нулевой вектор считается коллинеарным любому вектору.

Определение. Два вектора и называются равными ( ), если они коллинеарные, одинаково направлены и имеют одинаковые длины.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку пространства.

На рисунке 5.1 векторы образуют прямоугольник. Справедливо равенство , но . Векторы и — противоположные, .

Рис. 5.1.

Равные векторы называют также свободными.

Определение. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Если среди трех векторов хотя бы один нулевой или два любые коллинеарные, то такие векторы компланарны.