
- •Часть I
- •Часть I
- •Введение
- •I. Элементы линейной алгебры
- •§1. Матрицы
- •Основные понятия
- •Действия над матрицами
- •§2. Определители
- •Основные понятия
- •2.2. Свойства определителей
- •§3. Невырожденные матрицы
- •Основные понятия
- •Обратная матрица
- •3.3. Ранг матрицы
- •§4. Системы линейных уравнений
- •Основные понятия
- •Решение систем линейных уравнений. Теорема Кронекера-Капелли
- •Решение невырожденных линейных систем. Формулы Крамера
- •Решение систем линейных уравнений методом Гаусса
- •Системы линейных однородных уравнений
- •II. Элементы векторной алгебры
- •§5. Векторы
- •5.1. Основные понятия
- •5.2. Линейные операции над векторами
- •5.3. Проекция вектора на ось
- •5.4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
- •5.5. Действия над векторами, заданными проекциями
- •§6. Скалярное произведение векторов и его свойства
- •6.1. Определение скалярного произведения
- •6.2. Свойства скалярного произведения
- •6.3. Выражение скалярного произведения через координаты
- •6.4. Некоторые приложения скалярного произведения
- •§ 7. Векторное произведение векторов и его свойства
- •7.1. Определение векторного произведения
- •7.2. Свойства векторного произведения
- •7.3. Выражение векторного произведения через координаты
- •7.4. Некоторые приложения векторного произведения
- •§8. Смешанное произведение векторов
- •8.1. Определение смешанного произведения, его геометрический смысл
- •8.2. Свойства смешанного произведения
- •8.3. Выражение смешанного произведения через координаты
- •8.4. Некоторые приложения смешанного произведения
- •III. Аналитическая геометрия на плоскости
- •§9. Система координат на плоскости
- •9.1. Основные понятия
- •9.2. Основные приложения метода координат на плоскости
- •9.3. Преобразование системы координат
- •§10. Линии на плоскости
- •10.1. Основные понятия
- •10.2. Уравнения прямой на плоскости
- •10.3. Прямая линия на плоскости. Основные задачи
- •§11. Линии второго порядка на плоскости
- •11.1. Основные понятия
- •11.2. Окружность
- •11.3. Эллипс
- •11.4. Гипербола
- •IV. Аналитическая геометрия в пространстве
- •§12. Уравнения поверхности и линии в пространстве
- •12.1. Основные понятия
- •12.2. Уравнения плоскости в пространстве
- •12.3. Плоскость. Основные задачи
- •12.4. Уравнения прямой в пространстве
- •12.5. Прямая линия в пространстве. Основные задачи
- •12.6. Прямая и плоскость в пространстве. Основные задачи
- •12.7. Цилиндрические поверхности
- •12.8. Поверхности вращения. Конические поверхности
- •12.9. Канонические уравнения поверхностей второго порядка
- •V. Введение в анализ
- •§13. Множества. Действительные числа
- •13.1. Основные понятия
- •13.2. Числовые множества. Множество действительных чисел
- •13.3. Числовые промежутки. Окрестность точки
- •§14. Функции
- •14.1. Понятие функции
- •14.2. Числовые функции. График функции. Способы задания функций
- •14.3. Основные характеристики функции
- •14.4. Обратная функция
- •14.5. Сложная функция
- •14.6. Основные элементарные функции и их графики
- •§15. Последовательности
- •15.1. Числовая последовательность
- •15.2. Предел числовой последовательности
- •15.3. Предельный переход в неравенствах
- •15.4. Предел монотонной ограниченной последовательности. Число . Натуральные логарифмы
- •§16. Предел функции
- •16.1. Предел функции в точке
- •16.2. Односторонние пределы
- •16.3. Предел функции при
- •16.4. Бесконечно большая функция (б.Б.Ф.)
- •§17. Бесконечно малые функции (б.М.Ф.)
- •17.1. Определения и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •17.3. Основные теоремы о пределах
- •17.4. Признаки существования пределов
- •17.5. Первый замечательный предел
- •17.6. Второй замечательный предел
- •§18. Эквивалентные бесконечно малые функции
- •18.1. Сравнение бесконечно малых функций
- •18.2. Эквивалентные бесконечно малые и основные теоремы о них
- •18.3. Применение эквивалентных бесконечно малых функций
- •§ 19. Непрерывность функций
- •19.1. Непрерывность функции в точке
- •19.2. Непрерывность функции в интервале и на отрезке
- •19.3. Точки разрыва функции и их классификация
- •19.4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •19.5. Свойства функций, непрерывных на отрезке
- •Заключение
- •Библиографический список
- •Часть I
- •394026 Воронеж, Московский просп., 14
10.2. Уравнения прямой на плоскости
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.
Уравнение прямой с угловым коэффициентом.
Пусть
на плоскости
задана произвольная прямая, не
параллельная оси
.
Ее положение вполне определяется
ординатой
![]() точки
точки
![]() пересечения с осью
и углом
между осью
и прямой (см. рис. 10.10).
пересечения с осью
и углом
между осью
и прямой (см. рис. 10.10).
Под
углом
(![]() )
наклона
прямой понимается наименьший угол, на
который нужно повернуть вокруг точки
пересечения прямой и оси
против часовой стрелки ось
до ее совпадения с прямой.
)
наклона
прямой понимается наименьший угол, на
который нужно повернуть вокруг точки
пересечения прямой и оси
против часовой стрелки ось
до ее совпадения с прямой.
Возьмем
на прямой произвольную точку
(см. рис. 10.10). Проведем через точку
![]() ось
ось
![]() ,
параллельную оси
и одинаково с ней направленную. Угол
между осью
и прямой равен
.
В системе
,
параллельную оси
и одинаково с ней направленную. Угол
между осью
и прямой равен
.
В системе
![]() точка
имеет координаты
и
точка
имеет координаты
и
![]() .
Из определения
тангенса угла следует равенство
.
Из определения
тангенса угла следует равенство
![]() ,
т. е.
,
т. е.
![]() .
.
Введем
обозначение
![]() ,
получаем
уравнение
,
получаем
уравнение
![]() ,
(10.1)
,
(10.1)
которому
удовлетворяют координаты любой точки
прямой. Можно убедиться, что координаты
любой точки
![]() ,
лежащей вне данной прямой, уравнению
(10.1) не удовлетворяют.
,
лежащей вне данной прямой, уравнению
(10.1) не удовлетворяют.
Определение.
Число
![]() называется угловым
коэффициентом прямой,
а уравнение (10.2) — уравнением
прямой с угловым коэффициентом.
называется угловым
коэффициентом прямой,
а уравнение (10.2) — уравнением
прямой с угловым коэффициентом.
Если
прямая проходит через начало координат,
то
![]() и, следовательно, уравнение этой
прямой будет иметь вид
и, следовательно, уравнение этой
прямой будет иметь вид
![]() .
.
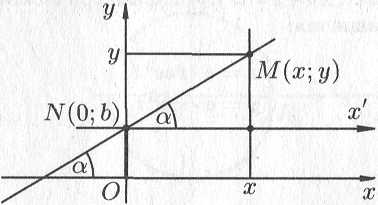
Рис. 10.10
Если
прямая параллельна оси
,
то
![]() ,
следовательно,
,
следовательно,
![]() и уравнение (10.1) примет вид
и уравнение (10.1) примет вид
![]() (10.2)
(10.2)
Если
прямая параллельна оси
,
то
![]() ,
уравнение (10.1) теряет смысл, т. к. для
нее угловой коэффициент
,
уравнение (10.1) теряет смысл, т. к. для
нее угловой коэффициент
![]() не существует. В этом случае уравнение
прямой будет иметь вид
не существует. В этом случае уравнение
прямой будет иметь вид
![]() ,
(10.3)
,
(10.3)
где
![]() — абсцисса точки пересечения прямой с
осью
.
Отметим, что уравнения (10.2) и (10.3) есть
уравнения первой степени.
— абсцисса точки пересечения прямой с
осью
.
Отметим, что уравнения (10.2) и (10.3) есть
уравнения первой степени.
Общее уравнение прямой.
Рассмотрим уравнение первой степени относительно и в общем виде
![]() ,
(10.4)
,
(10.4)
где , , — произвольные числа, причем и не равны нулю одновременно.
Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая.
Если
![]() ,
то уравнение (10.4) имеет вид
,
то уравнение (10.4) имеет вид
![]() ,
причем
,
причем
![]() ,
т.е.
,
т.е.
![]() — Это есть уравнение прямой, параллельной
оси
и проходящей через точку
— Это есть уравнение прямой, параллельной
оси
и проходящей через точку
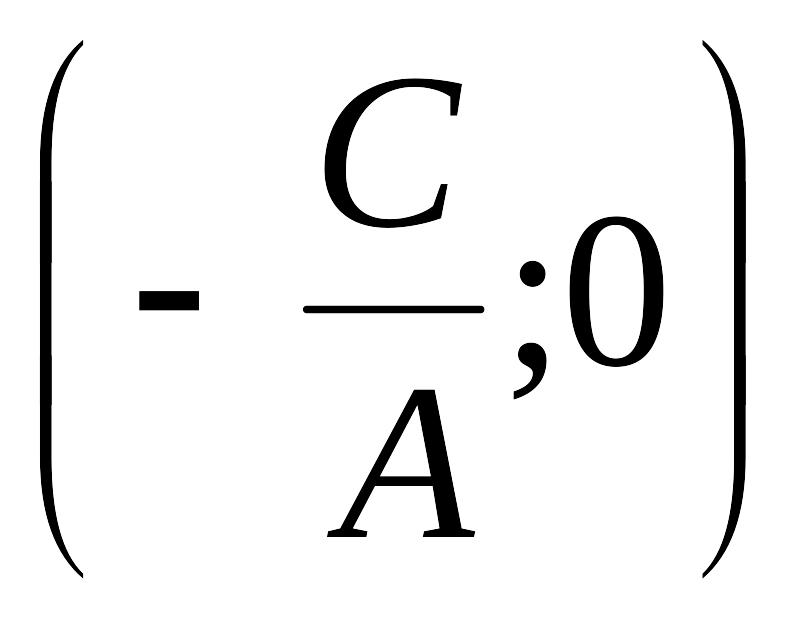 .
.
Если
![]() ,
то из уравнения (10.4) получаем
,
то из уравнения (10.4) получаем
![]() .
Это есть уравнение прямой с угловым
коэффициентом
.
Это есть уравнение прямой с угловым
коэффициентом
![]() .
.
Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой.
Некоторые частные случаи общего уравнения прямой:
если
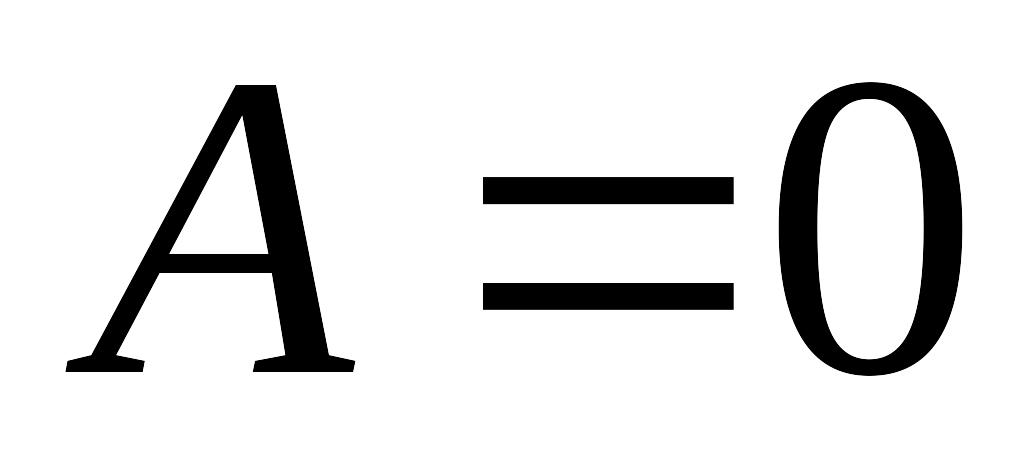 ,
то уравнение приводится к виду
,
то уравнение приводится к виду
 .
Это есть уравнение прямой, параллельной
оси
;
.
Это есть уравнение прямой, параллельной
оси
;если , то прямая параллельна оси ;
если
 ,
то получаем
,
то получаем
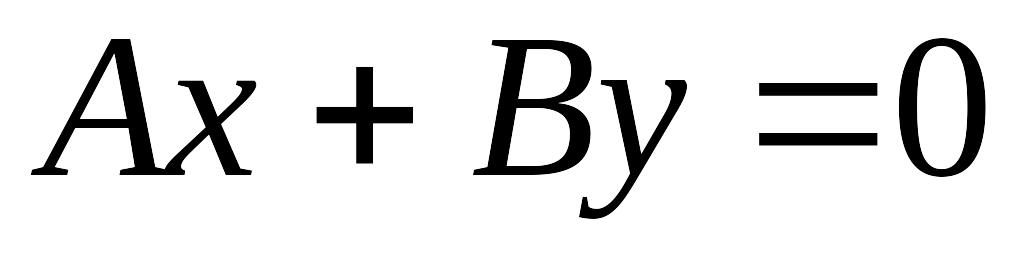 .
Уравнению удовлетворяют координаты
точки
.
Уравнению удовлетворяют координаты
точки
 ,
прямая проходит через начало координат.
,
прямая проходит через начало координат.
Уравнение прямой, проходящей через данную точку в данном направлении.
Пусть
прямая проходит через точку
![]() и ее направление характеризуется угловым
коэффициентом
.
Уравнение этой прямой можно записать
в виде
,
где
— пока неизвестная величина. Так как
прямая проходит через точку
,
то координаты точки удовлетворяют
уравнению прямой:
и ее направление характеризуется угловым
коэффициентом
.
Уравнение этой прямой можно записать
в виде
,
где
— пока неизвестная величина. Так как
прямая проходит через точку
,
то координаты точки удовлетворяют
уравнению прямой:
![]() .
Отсюда
.
Отсюда
![]() .
.
Подставляя
значение
в уравнение
,
получим искомое уравнение прямой
![]() ,
т. е.
,
т. е.
![]() (10.5)
(10.5)
Определение. Уравнение (10.5) с различными значениями называют также уравнениями пучка прямых с центром в точке .
Из этого пучка нельзя определить лишь прямую, параллельную оси .
Уравнение прямой, проходящей через две точки.
Пусть
прямая проходит через точки
![]() и
и
![]() .
Уравнение
прямой, проходящей через точку
.
Уравнение
прямой, проходящей через точку
![]() ,
имеет вид
,
имеет вид
![]() ,
(10.6)
,
(10.6)
где — пока неизвестный коэффициент.
Так
как прямая проходит через точку
,
то координаты этой точки должны
удовлетворять уравнению (10.6):
![]() .
Отсюда находим
.
Отсюда находим
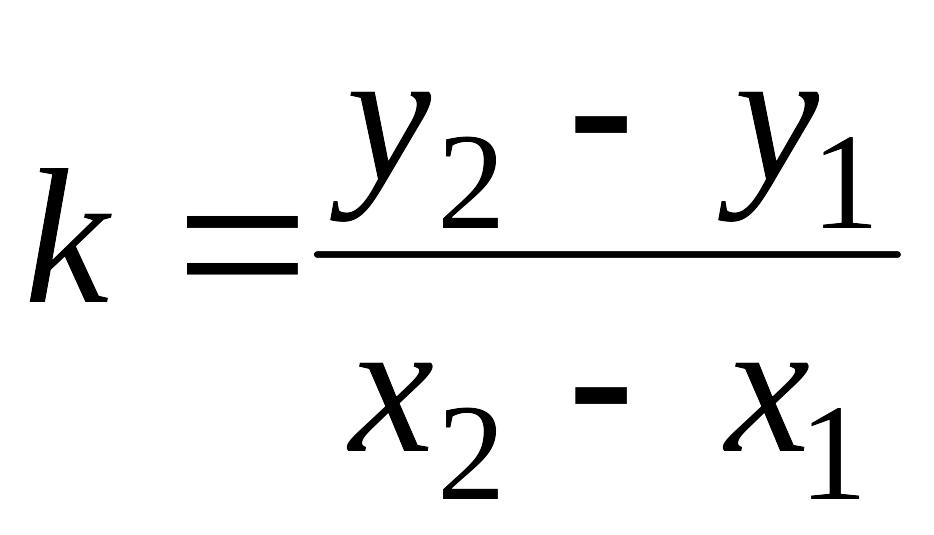 .
Подставляя найденное значение
в уравнение (10.6), получим уравнение
прямой, проходящей через точки
и
.
Подставляя найденное значение
в уравнение (10.6), получим уравнение
прямой, проходящей через точки
и
![]() :
:
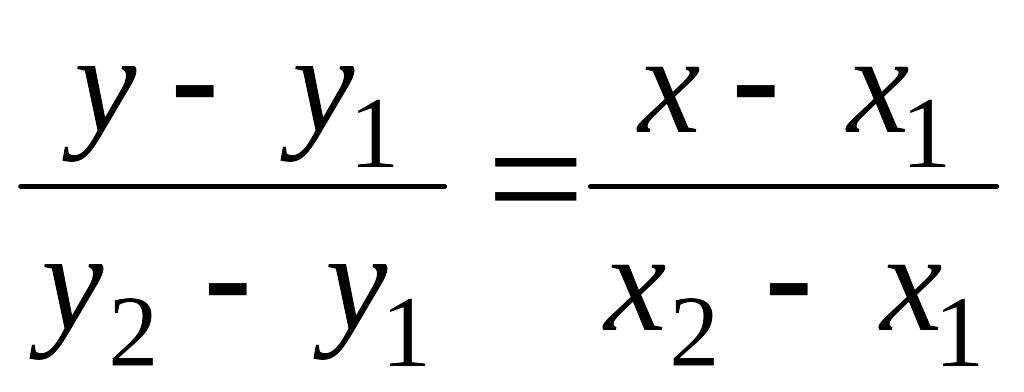 (10.7)
(10.7)
Предполагается,
что в этом уравнении
![]() ,
,
![]() .
.
Если
![]() ,
то прямая, проходящая через точки
и
параллельна оси ординат. Ее уравнение
имеет вид
,
то прямая, проходящая через точки
и
параллельна оси ординат. Ее уравнение
имеет вид
![]() .
.
Если
![]() ,
то уравнение прямой может быть записано
в виде
,
то уравнение прямой может быть записано
в виде
![]() ,
прямая
,
прямая
![]() параллельна оси абсцисс.
параллельна оси абсцисс.
Уравнение прямой в отрезках.
Пусть
прямая пересекает ось
в точке
![]() ,
а ось
— в точке
,
а ось
— в точке
![]() (см. рис. 10.11). В этом случае уравнение
(10.7) примет вид
(см. рис. 10.11). В этом случае уравнение
(10.7) примет вид
![]() ,
,
т.е.
![]()
Это уравнение называется уравнением прямой в отрезках, так как числа и указывают, какие отрезки отсекает прямая на осях координат.
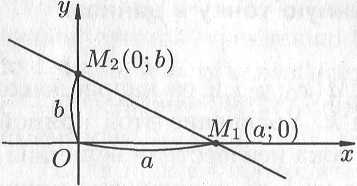
Рис. 10.11
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Найдем
уравнение прямой, проходящей через
заданную точку
![]() перпендикулярно данному ненулевому
вектору
перпендикулярно данному ненулевому
вектору
![]() .
.
Возьмем
на прямой произвольную точку
и рассмотрим вектор
![]() (см. рис. 10.12). Поскольку векторы
(см. рис. 10.12). Поскольку векторы
![]() и
и
![]() перпендикулярны, то их скалярное
произведение равно нулю:
перпендикулярны, то их скалярное
произведение равно нулю:
![]() ,
то есть
,
то есть
![]() (10.8)
(10.8)

Рис. 10.12
Определение. Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Вектор , перпендикулярный прямой, называется нормальным вектором этой прямой.
Уравнение (10.8) можно переписать в виде
(10.9)
где
и
— координаты
нормального вектора,
![]() — свободный член. Уравнение (10.9) есть
общее уравнение прямой (см. (10.4)).
— свободный член. Уравнение (10.9) есть
общее уравнение прямой (см. (10.4)).
Полярное уравнение прямой.
Найдем
уравнение прямой в полярных координатах.
Ее положение можно определить, указав
расстояние
![]() от полюса
до данной прямой и угол
между полярной осью
от полюса
до данной прямой и угол
между полярной осью
![]() и осью
,
проходящей через полюс
перпендикулярно данной прямой (см. рис.
10.13).
и осью
,
проходящей через полюс
перпендикулярно данной прямой (см. рис.
10.13).
Для любой точки на данной прямой имеем:
![]()
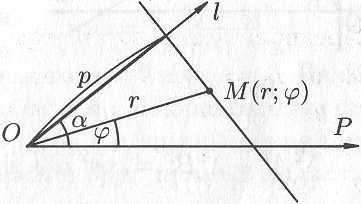
Рис. 10.13
С другой стороны,
![]() .
.
Следовательно,
![]() (10.10)
(10.10)
Полученное уравнение (10.10) и есть уравнение прямой в полярных координатах.
Нормальное уравнение прямой.
Пусть прямая определяется заданием и (см. рис. 10.14). Рассмотрим прямоугольную систему координат . Введем полярную систему, взяв за полюс и за полярную ось. Уравнение прямой можно записать в виде
![]() ,
т. е.
,
т. е.
![]() .
.
Но,
в силу формул, связывающих прямоугольные
и полярные координаты, имеем:
![]() ,
,
![]() .
Следовательно, уравнение (10.10) прямой в
прямоугольной системе координат примет
вид
.
Следовательно, уравнение (10.10) прямой в
прямоугольной системе координат примет
вид
![]() (10.11)
(10.11)
Уравнение (10.11) называется нормальным уравнением прямой.
Покажем, как привести уравнение (10.4) прямой к виду (10.11).
Умножим
все члены уравнения (10.4) на некоторый
множитель
![]() .
Получим
.
Получим
![]() .
Это уравнение должно обратиться в
уравнение (10.11). Следовательно, должны
выполняться равенства:
.
Это уравнение должно обратиться в
уравнение (10.11). Следовательно, должны
выполняться равенства:
![]() ,
,
![]() ,
,
![]() .
Из первых двух равенств находим
.
Из первых двух равенств находим
![]() , т.е.
, т.е.
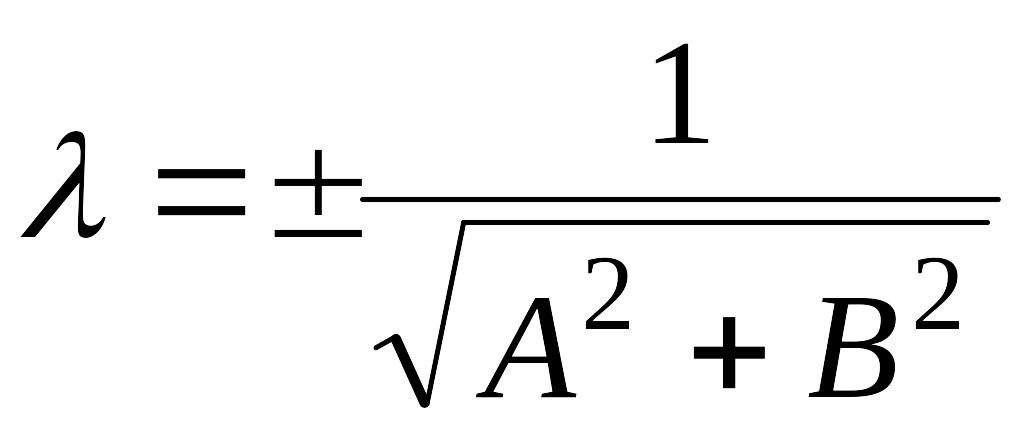 .
.
Множитель называется нормирующим множителем. Согласно третьему равенству знак нормирующего множителя противоположен знаку свободного члена общего уравнения прямой.
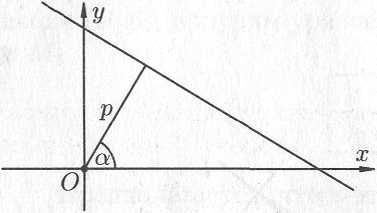
Рис. 10.14
Пример
10.2.
Привести
уравнение
![]() к нормальному виду.
к нормальному виду.
Решение. Находим нормирующий множитель
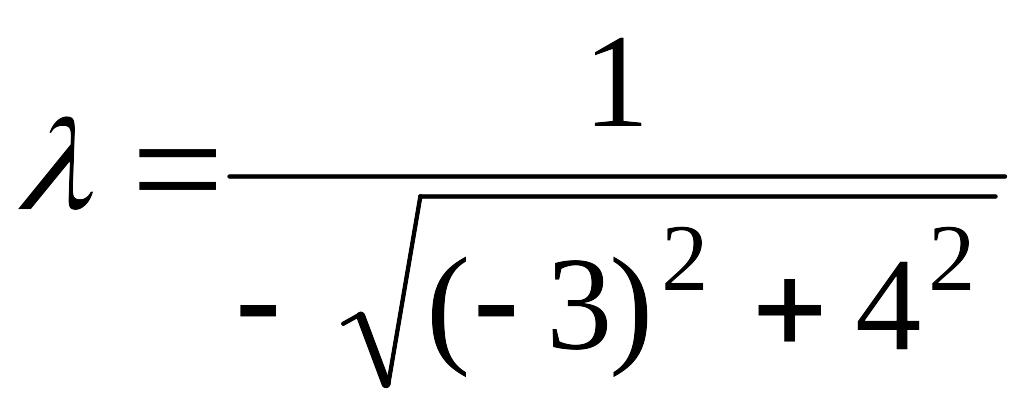 .
.
Умножая данное уравнение на , получим искомое нормальное уравнение прямой:
![]() .
.
