Учебное пособие 1623

ВВЕДЕНИЕ

Цель пособия - помочь студентам научиться самостоятельно решать задачи по курсу высшей математики, при условии, что изучение теории должно выполняться по рекомендованному в программе учебнику и конспекту лекций. В пособии рассмотрены следующие вопросы теории функций нескольких переменных: функции от двух или n переменных, область определения, геометрическое толкование, частные производные и дифференцирование сложных функций, неявные функции и их дифференцирование, полный дифференциал и его применение к приближенным вычислениям. Пособие предназначено главным образом для использования во время практических занятий по высшей математике, в качестве задачника для самостоятельной работы и при подготовке к контрольным работам.

Каждый параграф начинается с краткого теоретического введения, приводятся основные определения, теоремы без доказательств, главнейшие формулы, методы и способы решения задач. Решение типовых примеров и задач в параграфе, как правило, расположено по возрастающей трудности.

Характерной особенностью является включение решений задач вычислительного характера, что позволяет развивать необходимые навыки и умение для студентов инженерных специальностей. Кроме того, значительное внимание уделено методам решения прикладных задач с физическим смыслом.

Часть задач была заимствована из сборников задач по курсу математического анализа: Берман Г.Н., Минорский В.П., Демидович Б.П., Бугров Я.С., Никольский Я.С.

Пособие включает задания для типового расчета по дифференциальному исчислению по основным разделам, изучаемым в курсе высшей математики в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования по направлению 280100 «Безопасность жизнедеятельности».

3

1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

1.1. Понятие о функции нескольких переменных. Область определения

10. Если в силу некоторого закона каждой совокупности n чисел (x, y, z,...,t) из некоторого множества E ставится в

соответствие определенное значение переменной и, то и

функции, множество E - областью определения функции. Частным значением функции называется значение

функции в некоторой точке M0 (x0 , y0 , z0 ,...,t0 ) и обозначается

f (M0 ) = f (x0 , y0 , z0 ,...,t0 ) .

Областью определения функции называется множество всех значений аргументов, которым соответствуют какие-либо действительные значения функции.

20. Функция двух переменных z = f (x, y) в пространстве

представляется некоторой поверхностью. То есть, когда точка с координатами x, y пробегает всю область определения

функции, расположенную в плоскости xOy , соответствующая

пространственная точка, вообще говоря, описывает поверхность.

Функцию трех переменных u = f (x, y, z) рассматривают как функцию точки некоторого множества точек трехмерного

совокупность точек плоскости xOy , в которых функция имеет

4

одинаковые значения, и обозначается f (x, y) = С . Различным значениям С соответствуют различные поверхности уровня.

этих точек в выражение функции. Тогда частное значение

б) f (2x + y,2x − y) = xy .

5

Решение. а) Обозначим u = xy , υ = x − y . Разрешая эти

уравнения относительно x, y , будем иметь x = 1υ−u , y = 1u−υu .

Представим заданную функцию через новые переменные

Если переименовать переменные u,υ в x, y , то получим

f (x, y) = 11+− xx y2 .

б) Обозначим u = 2x + y , υ = 2x − y . Откуда x = 14 (u +υ) , y = 12 (u −υ) .

Запишем заданную функцию через новые переменные f (u,υ) = 18 (u2 −υ2 ) .

Если переименовать переменные u,υ в x, y , будем иметь

или x2 + y2 >1, т.е. областью существования данной функции

является часть плоскости вне единичного круга с центром в начале координат.

6

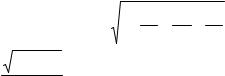
б) Функция z принимает вещественные значения при

существования функции является открытый эллипс. Граница эллипса не входит в область существования функции.

−x ≤ y ≤ x . Областью существования функции является часть

областью существования функции является внутренняя часть правого вертикального угла, образованного биссектрисами, включая сами биссектрисы.

д) Функция определена, если xy > 0 , т.е. областью

существования функции является часть плоскости, лежащая внутри первого и третьего координатных углов, исключая границы.

е) Функция принимает вещественные значения при условии sinϕ ≥ 0 , т.е. 0 ≤ϕ ≤π , ρ - любое. Областью

определения будет верхняя полуплоскость. 1.4. Найти область определения функций:

z > x2 + y2 , т.е. областью существования функции u является

часть пространства, заключенная внутри параболоида, исключая сам параболоид.

7

б) Функция зависит от трех переменных и принимает

является часть пространства, заключенная внутри трехосного эллипсоида, включая границу.

в) Функция зависит от трех переменных и определена,

1.5. Найти линии и поверхности уровня функций:

а) z = x2 − y2 ; б) u = x2 + y2 + z2 .

Решение. а) Уравнение линий уровня имеет вид x2 − y2 = C , т.е. линии уровня равносторонние гиперболы.

При C > 0 вершины гиперболы расположены на оси Ox , при C < 0 - на оси Oy .

б) Уравнение поверхностей уровня имеет вид x2 + y2 + z2 = C , т.е. поверхности уровня – это семейство сферических поверхностей с центром в начале координат.

1.2. Предел функции нескольких переменных. Непрерывность

10. Число A называется пределом функции f (M ) при M → M0 , если для любого числа ε > 0 всегда найдется такое

8

Предел обозначают lim f (M ) = A . В случае функции

M →M 0

двух переменных lim f (x, y) = A .

x→x0 y→y0

20. Теоремы о пределах. Если функции f1 (M ) и f2 (M ) при M → M0 стремятся каждая к конечному пределу, то

если она удовлетворяет следующим трем условиям: а) функция f (M ) определена в точке M0 ;

б) существует предел lim f (M ) ;

M →M0

в) lim f (M ) = f (M0 ) .

M →M0

Если в точке M0 нарушено хотя бы одно из этих

условий, то функция в этой точке терпит разрыв. Точки разрыва могут образовывать линии разрыва, поверхности разрыва и т.д. Функция f (M ) называется непрерывной в

области G , если она непрерывна в каждой точке этой области. Из определения непрерывности функции в точке следует, что бесконечно малым приращениям аргументов

соответствует бесконечно малое приращение функции.

9

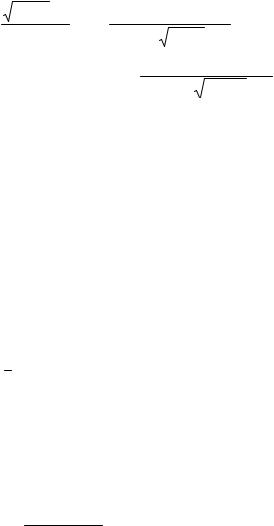
Решение. а) Преобразуем предел следующим образом

Таким образом, предел имеет различные значения в зависимости от выбранного k , т.е. функция не имеет предела.

г) Воспользуемся вторым замечательным пределом

1

б) u = 1 . x2 + y2 − z2

Решение. а) Функция z = ln(x2 + y2 ) терпит разрыв в точке x = 0 , y = 0 .

Следовательно, точка O(0,0) является точкой разрыва.

10