Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1623

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2218 19 20 21 22 > Следующая >>>

5.	y′		=	y 2 e2 x − xe2 y
						.
				x 2 e2 y − ye2 x
7.	y′		=	y cos x +sin(x − y)			.
				sin(x − y) −sin x
9.	y	′			y
			= − x .

6. y′ =

8. y′ =

10. y′ =

1+ y 2 . y 2

y(2x +e xy −cos xy) . x(cos xy −e xy − x)

2 y −2x −1 .

2 y −2x +1

Касательная плоскость и нормаль к поверхности

Постановка задачи. Найти уравнение касательной и нормали к поверхности, заданной уравнением

F(x, y, z) = 0 ,

в точке M (x0 , y0 , z0 ) .

План решения.

Нормальный вектор к поверхности, заданной уравнением

F(x, y, z) = 0

в точке M (x0 , y0 , z0 ) определяется формулой

n = grad F

∂F

∂x

∂y

∂z

Следовательно, уравнение касательной плоскости к данной поверхности в точке M (x0 , y0 , z0 ) есть

Fx′

M (x + x0 ) + Fy′

M (x0 , y0 , z0 )( y − y0 ) + Fz′

M (z − z0 ) = 0

(13)

и уравнения нормали –

x − x0

y − y0

z − z0

(14)

Fx′

Fy′

Fz′

1. Находим частные производные Fx′, Fy′, Fz′ в точке

M (x0 , y0 , z0 ) .

171

2.Подставляем найденные значения в уравнения (13) и

(14)и записываем ответ.

Замечание. Если заданы только значения x0 и y0 , то координата z0 точки М определяется из условия, что точка М принадлежит данной поверхности , т.е. F(x0 , y0 , z0 ) = 0 .

Пример. Найти уравнение касательной плоскости и

нормали к поверхности, заданной уравнением z = xy

в точке М(1, 1).

Решение. Запишем уравнение поверхности в виде ху-z=0,

т.е. F = xy − z.

Координаты точки М: x0 =1 и y0 =1. Координаты z0

определяем из условия, что точка М принадлежит данной поверхности, т.е. F(1, 1, z0 ) = 0 . Получаем z0 =1.

1. Находим частные производные

Fx′,

Fy′, Fz′

в точке

М(1, 1, 1):

Fx′

(1,1,1) = y

(1,1,1) =1,

Fy′

(1,1,1) = x

(1,1,1)

=1,

Fz′

(1,1,1)

= −1.

2. Подставляя найденные значения в уравнения (13) и (14),

получаем уравнение касательной плоскости

1(x −1) +1( y −1) −1(z −1) = 0

и уравнение нормали

y −1

x −1

z −1

Ответ. Уравнение касательной плоскости: x + y − z −1 = 0. Уравнение нормали: x −1 = y −1 =1− z.

Условия задач. Найти уравнения касательной плоскости и нормали к поверхности в заданной точке М.

1.	z = x 2 + y 2 ,						M (1, −2, 5).
2.	x 2	+	y 2	−	z	2	= 0, M (4, 3, 4).
	16		9		8

172

3.z = sin x cos y, M (π / 4, π / 4, 1/ 2).

4.z = e x cos y , M (1, π, 1/ e).

5.z = y tg x, M (π / 4, 1, 1).


6.	z = arctg(x / y),				M (1, 1, π / 4).
7.	x( y + z)(z − xy) = 8,					M (2, 1, 3).
8.	2 x / z + 2 y / z = 8,				M (2, 2, 1).
9.	x 2	+ y 2	+ z 2	−16 = 0,		M (2, 2, 2 2).
10.	x 2	+ y 2	− z 2	= −1, M (2, 2, 3).

Ответы.

x −1

y + 2

z −5

1. 2x −2 y − z −5 = 0,

−4

−1

2. 3x + 4 y −6Z = 0,

x −4

y −3

z −4

−6

x − y −2z +1 = 0,

x −π / 4

y −π / 4

z −1 / 2

y −π

−1

−2

x +ez −2 = 0,

x −1

z −1/ e

y −1

5. 2x + y − z −

= 0,

x −π / 4

z −1

y −1

−1

x − y −2z +

= 0,

x −1

z −π / 4

−1

−2

7. 2x +7 y −5z + 4 = 0,

x −2

y −1

z −3

−5

x + y −4z = 0,

x −2

y −2

z −1

−4

x + y + 2z −8 = 0,

x −2

y −2

= z −2 2 .

10. 2x + 2 y −3z +1 = 0,

x −2

y −2

z −3

−3

173

Экстремум функции двух переменных

Постановка задачи. Найти стационарные точки функции z = z(x, y) и исследовать их характер.

План решения.

1. Стационарными точками функции нескольких переменных называются точки, в которых все ее частные производные равны нулю. Следовательно, чтобы найти стационарные точки функции z(x, y) , нужно решить систему двух уравнений с двумя неизвестными

z′x (x, y) = 0,z′y (x, y) = 0.

Решая эту систему уравнений, находим стационарные точки функции z(x, y) : M1 (x1 , y1 ), M 2 (x2 , y2 ),…, M n (xn , yn ).

2. Для того чтобы исследовать характер стационарных точек, воспользуемся достаточными условиями экстремума функции двух переменных.

Пусть функция z = z(x, y) определена и имеет непрерывные частные производные второго порядка в стационарной точке

M (x0 , y0 )				(т.е. z′x (x0 , y0 ) = z′y (x0 , y0 ) = 0 ). Тогда если в этой
точке:
а)	′′	′′		′′	2	> 0			, то М – точка экстремума, причем при
	z xx z yy		−(z xy )
′′									′′
z xx	> 0 - точка минимума, при z xx < 0 - точка максимума;
б)	′′	′′		′′	2	< 0			, то М не является точкой экстремума;
	z xx	z yy	−(z xy )
в)		′′	′′	′′			2	= 0 , то требуется дополнительное
	z xx z yy −(z xy )

исследование (например, по определению).

174

3. Вычисляем производные	второго порядка функции
z(x, y) .
4. В каждой стационарной точке вычисляем выражение
′′ ′′	′′	2
z xx z yy −(z xy )

и определяем его знак.

Анализируем полученные результаты и записываем ответ.

Пример. Найти стационарные точки функции

z= x3 + y 3 −3xy

иисследовать их характер.

Решение.

1. Вычисляем частные производные

z′x = 3x 2 −3y, z′y = 3y 2 −3x.

2. Для того чтобы найти стационарные точки функции, решаем систему двух уравнений с двумя неизвестными

3x 2 −3y = 0,

3y 2 −3x = 0.

Получаем два		решения:	x1 = 0 ,		y1	= 0 и	x2 =1, y2 =1.
Следовательно,		стационарные				точки	функции
z = x3 + y 3 −3xy :		M 1 (0, 0) и M 2 (1, 1) .
3.	Вычисляем производные второго порядка:
		′′	′′	= −3,	′′	= 6 y .
	z xx = 6x,		z xy	= −3,	z yy	= 6 y .
4.	В каждой стационарной точке вычисляем выражение
		′′	′′	′′	2
		z xx z yy −(z xy )

175

и определяем его знак. В точке М1(0, 0):

′′	′′	′′	′′ ′′	′′	2	= −6 < 0.
z xx (0, 0) = 0, z xy		(0, 0) = −3, z yy (0, 0) = 0 z xx z yy −(z xy )
Следовательно,		точка М2(1, 1) является точкой экстремума.
	′′	= 6 > 0, то M 2 (1, 1) - точка минимума.
Так как z xx (1, 1)
Ответ. Функция z = x3 + y 3 −3xy			имеет две стационарные
точки	M 1 (0, 0) и M 2 (1, 1) . В точке		M 1 (0, 0) экстремума нет,

M 2 (1, 1)		- точка минимума.
	Условия задач.
1.	z = x 2	− xy + y 2 .	2.	z = x 2 − xy − y 2 .
3.	z = x 2	−2xy + 2 y 2 + 2x.	4.	z = x3 + y 3 − x 2	−2xy − y 2 .
5. z = x3 −2 y 3 −3x +6 y.			6.	z = 4x + 2 y − x 2	− y 2 .
7.	z = x3 + y 3 −15xy.		8.	z = x 2 + xy + y 2	−3x −6 y.
9.	z = x 2	+ 4 y 2 −2xy + 4.	10.	z = x / y +1/ x + y.

Ответы.

1.М (0, 0) – стационарная точка. М (0, 0) – точка минимума, zmin = z(0, 0) = 0.

2.М (0, 0) – стационарная точка. В точке М (0, 0) экстремума нет.

3.М (-2, -1) – стационарная точка. М (-2, -1) – точка минимума, zmin = z(−2, −1) = −2.

176

4. М1 (0, 0), М2 (4/3, 4/3) – стационарные точки. М (0, 0) –

точка минимума, zmin = z(0, 0) = 0. М (4/3, 4/3) – точка минимума, zmin = z(4 / 3, 4 / 3) = −67 / 27.

5. М1 (1, 1), М2 (-1, -1), М3 (-1, 1), М4 (1, -1) – стационарные точки. В точках М1 (1, 1), М2 (-1, -1) экстремума нет. М3 (-1, 1)

– точка максимума, zmin = z(−1, 1) = 6. М4 (1, -1) – точка минимума, zmin = z(1, −1) = −6.

6.М (2, 1) – стационарная точка. М (2, 1) – точка максимума, zmin = z(2, 1) = 5.

7.М1 (0, 0), М2 (5, 5) – стационарные точки. В точке М1 (0, 0)

экстремума нет. М2 (5, 5) – точка минимума, zmin = z(5, 5) = −125.

8.М (0, 3) – стационарная точка. М (0,3) – точка минимума, zmin = z(0, 3) = −9.

9.М (0,0) – стационарная точка. М (0, 0) – точка минимума, zmin = z(0, 0) = 4.

10.М (1, 1) – стационарная точка. М (1, 1) –точка минимума, zmin = z(1, 1) = 3.

177

4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Геометрическое место точек трехмерного пространства, координаты которых в некоторой прямоугольной системе

координат (O, e1, e2 , e3 ) удовлетворяют уравнению

a x2	+ 2a xy + a y2		+ 2a xz + a z2		+ 2a yz+
11	12	22	13	33		23
		+2a1x + 2a2 y + 2a3z + a = 0,				(1)

где хотя бы один из коэффициентов aij не равен нулю,

называется поверхностью второго порядка.

Для любой поверхности второго порядка существует прямоугольная система координат (O, e1 , e2 , e3 ), в которой

уравнение этой поверхности имеет один из следующих 17 видов:

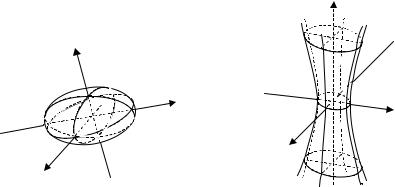
1) эллипсоид

=1 (рис.4.1);

2) мнимый эллипсоид

= −1 ;

3) однополостный гиперболоид

−

=1 (рис. 4.2);

o b

Рис.4.1

Рис. 4.2

178

4)двуполостный гиперболоид

−

конус

−

= 0 (рис. 4.4);

мнимый конус

= 0 ;

эллиптический параболоид

= 2z

8) гиперболический параболоид x2 − y2 = a2 b2

	o	o
	x	y
	x	y
		y

= −1 (рис. 4.3);

(рис. 4.5);

2z (рис. 4.6);

Рис. 4.3

Рис. 4.4

179

Рис. 4.5

Рис. 4.6

9) эллиптический цилиндр

=1 (рис.4.7);

10) мнимый эллиптический цилиндр

= −1 ;

11) гиперболический цилиндр

−

=1 (рис.4.8);

o	o
x	x
y	y
y
Рис.4.7	Рис. 4.8

12) параболический цилиндр y2 = 2 px, p > 0 (рис.4.9);

180

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2218 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.52 Mб2Учебное пособие 1619.pdf
#
30.04.2022308.13 Кб2Учебное пособие 162.pdf
#
30.04.20221.53 Mб2Учебное пособие 1620.pdf
#
30.04.20221.53 Mб4Учебное пособие 1621.pdf
#
30.04.20221.53 Mб1Учебное пособие 1622.pdf
#
30.04.20221.55 Mб2Учебное пособие 1623.pdf
#
30.04.20221.55 Mб5Учебное пособие 1624.pdf
#
30.04.20221.55 Mб2Учебное пособие 1625.pdf
#
30.04.20221.55 Mб2Учебное пособие 1626.pdf
#
30.04.20221.55 Mб9Учебное пособие 1627.pdf
#
30.04.20221.56 Mб3Учебное пособие 1628.pdf