19.5. Свойства функций, непрерывных на отрезке

Непрерывные на отрезке функции имеют ряд важных свойств. Сформулируем их в виде теорем, не приводя доказательств.

Теорема 19.4 (Вейерштрасса). Если функция непрерывна на отрез­ке, то она достигает на этом отрезке своего наибольшего и наимень­шего значений.

Изображенная на рисунке 19.5 функция непрерывна на отрезке , принимает свое наибольшее значение в точке , а наименьшее — в точке . Для любого имеет место нера­венство .

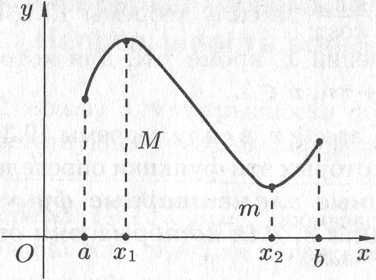
Рис. 19.5

Следствие 19.1. Если функция непрерывна на отрезке, то она огра­ничена на этом отрезке.

Теорема 19.5 (Больцано-Коши). Если функция непре­рывна на отрезке и принимает на его концах неравные значения и , то на этом отрезке она принимает и все проме­жуточные значения между и .

Геометрически теорема очевидна (см. рис. 19.6).

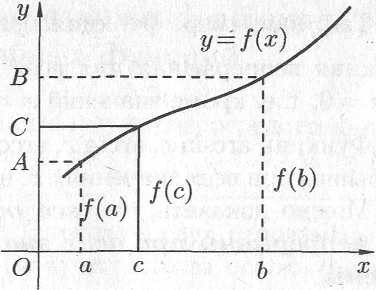
Рис. 19.6

Для любого числа , заключенного между и , найдется точка с внутри этого отрезка такая, что . Прямая пересечет график функции по крайней мере в одной точке.

Следствие 19.2. Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то внутри отрезка найдется хотя бы одна точка , в которой данная функция обращается в нуль: .

Геометрический смысл теоремы: если график непрерывной функ­ции переходит с одной стороны оси на другую, то он пересекает ось .

Следствие 19.2 лежит в основе так называемого «метода половин­ного деления», который используется для нахождения корня уравнения .

Утверждения теорем 19.4 и 19.5, вообще говоря, делаются невер­ными, если нарушены какие-либо из ее условий: функция непрерывна не на отрезке , а в интервале , либо функция на отрезке имеет разрыв.

Рисунок 126 показывает это для следствия теоремы 19.5: график разрывной функции не пересекает ось .

Пример 19.5. Определить с точностью до = 0,00001 корень уравнения , принадлежащий отрезку [0;1], применив метод половинного деления.

Решение. Обозначим левую часть уравнения через .

Шаг 1. Вычисляем и , где , .

Шаг 2. Вычисляем .

Шаг 3. Вычисляем . Если , то — корень уравне­ния.

Шаг 4. При если , то полагаем , , иначе полагаем , .

Шаг 5. Если то задача решена. В качестве искомого корня (с заданной точностью ) принимается величина . Ина­че процесс деления отрезка пополам продолжаем, возвращаясь к шагу 2.

В результате произведенных действий получим: = 0,29589.

Заключение

Данное учебное пособие содержит основные сведения из разделов курса высшей математики, таких как: элементы линейной алгебры, элементы векторной алгебры, аналитическая геометрия на плоскости, аналитическая геометрия в пространстве, введение в математический анализ.

Последовательное изложение учебного материала от более простых понятий к более сложным, должны способствовать глубокому усвоению студентами дисциплины «Высшая математика». Рассмотренные конкретные примеры позволяют изучить все существенные особенности, которые могут возникать при решении задач.