15.4. Предел монотонной ограниченной последовательности. Число . Натуральные логарифмы

Не всякая последовательность имеет предел. Сформулируем без доказательства признак существования предела последовательности.

Теорема 15.3 (Вейерштрасса). Всякая монотонная ограниченная по­следовательность имеет предел.

В качестве примера на применение этого признака рассмотрим по­следовательность , .

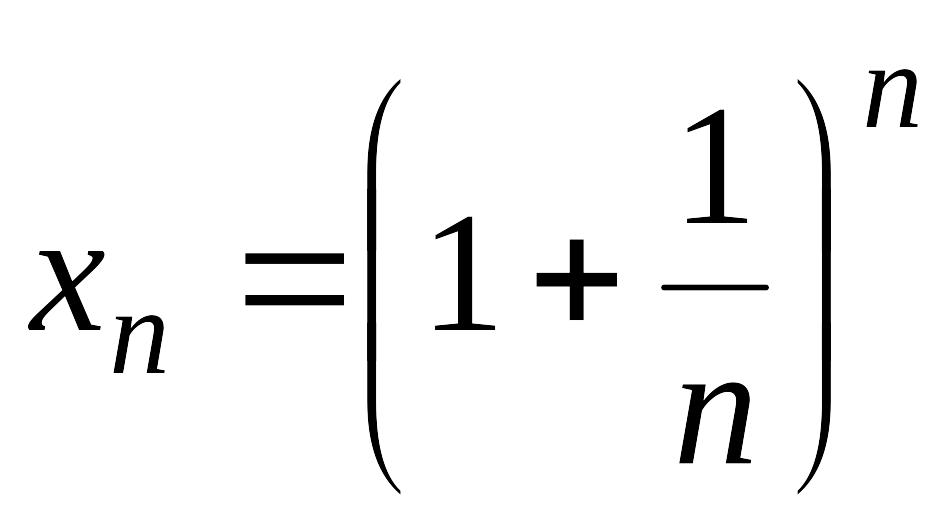По формуле бинома Ньютона

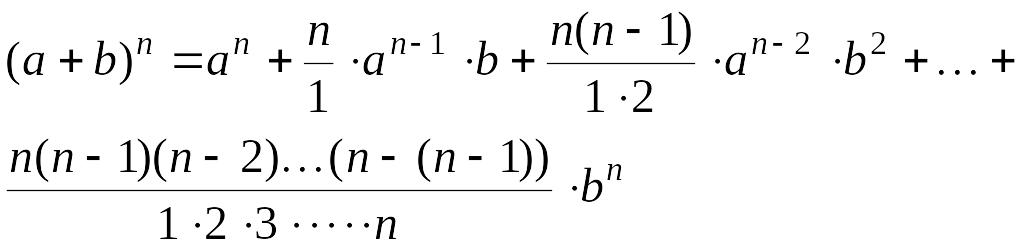
Полагая , , получим

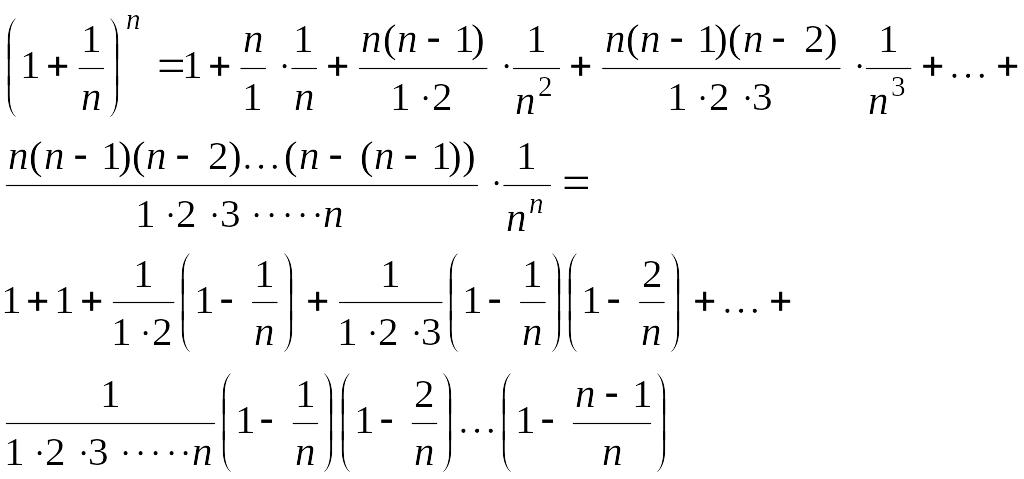
или

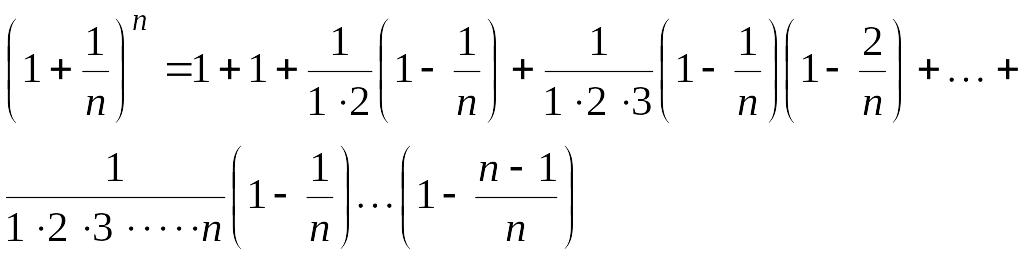
Из равенства (15.3) следует, что с увеличением число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении число убывает, поэтому величины 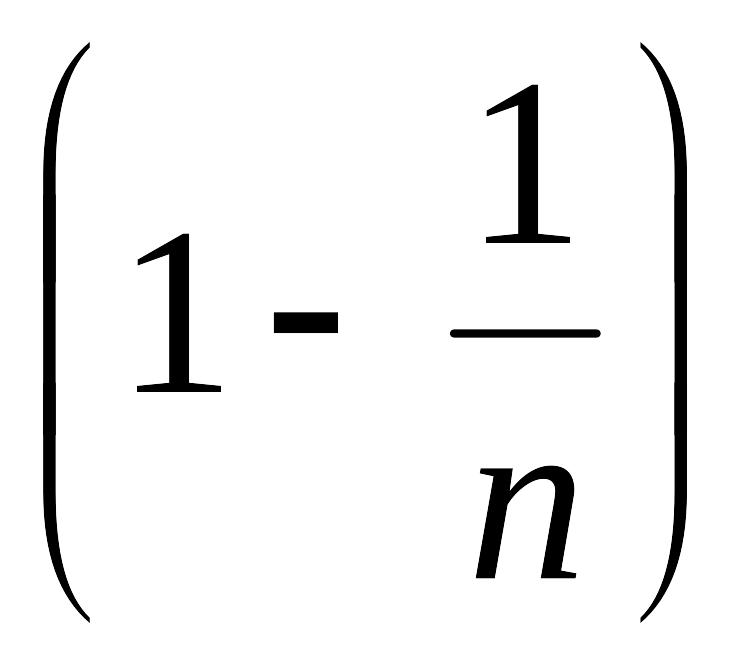, , 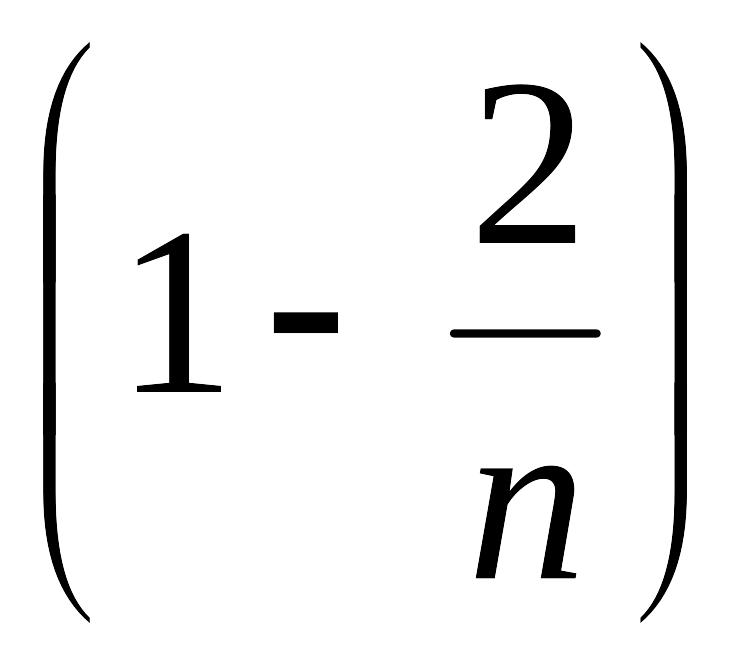… возрастают.

Поэтому последовательность 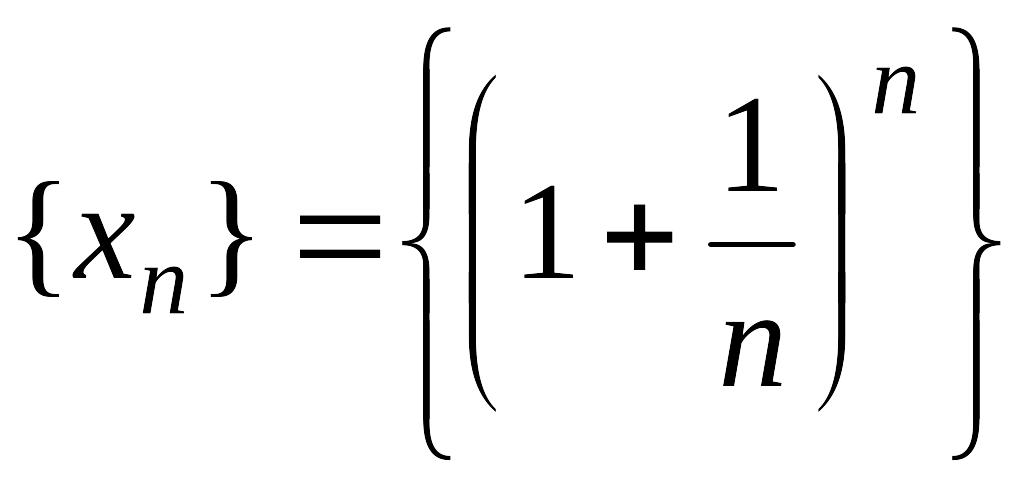— возрастающая, при этом

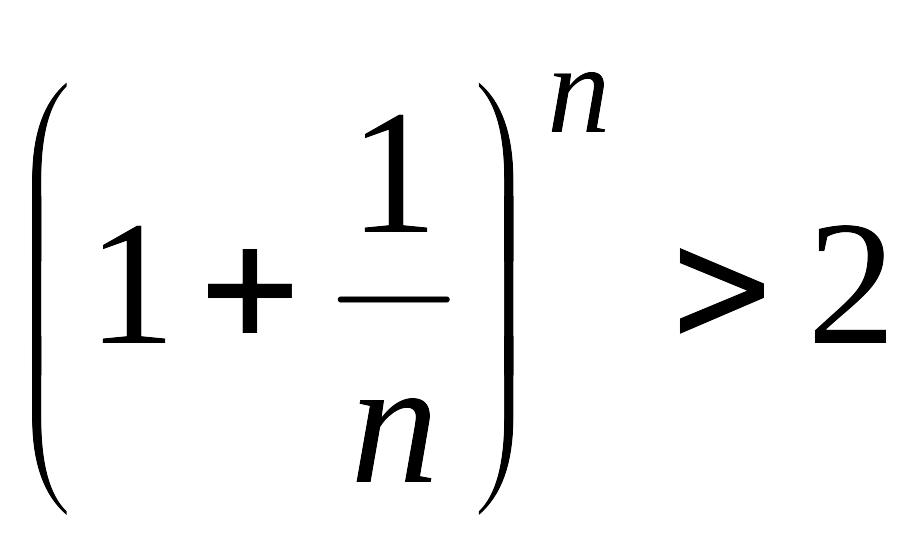. (15.4)

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства (15.3) на единицу; правая часть увеличится, получим нера­венство

.

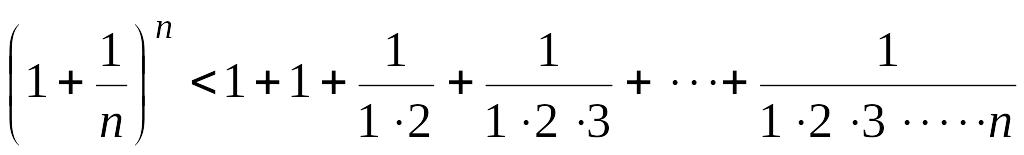Усилим полученное неравенство, заменив числа 3, 4, 5,…, стоящие в знаменателях дробей, числом 2:

.

Сумму в скобке найдем по формуле суммы членов геометрической про­грессии:

.

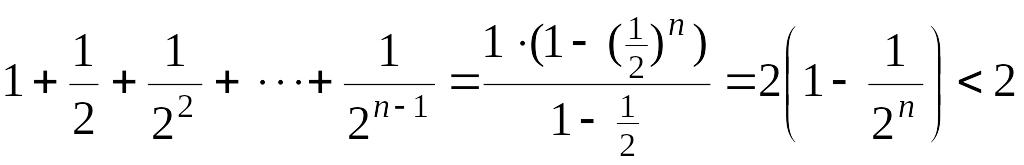Поэтому

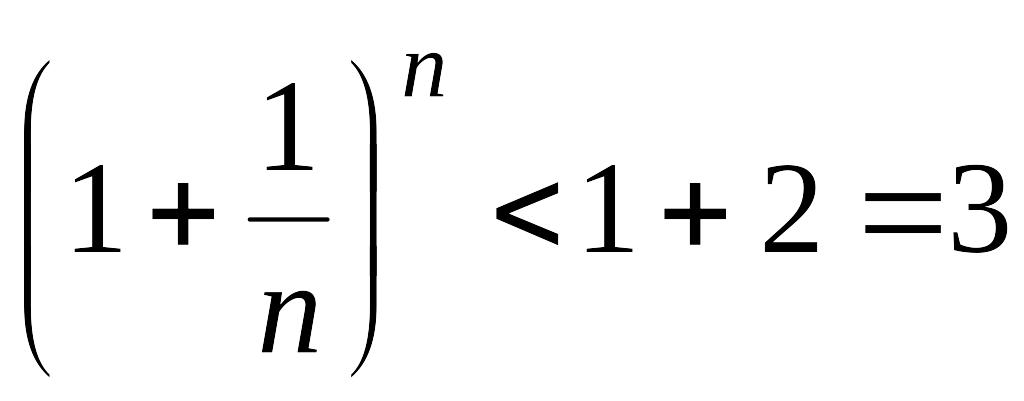. (15.5).

Итак, последовательность ограничена, при этом для выполня­ются неравенства (15.4) и (15.5):

.

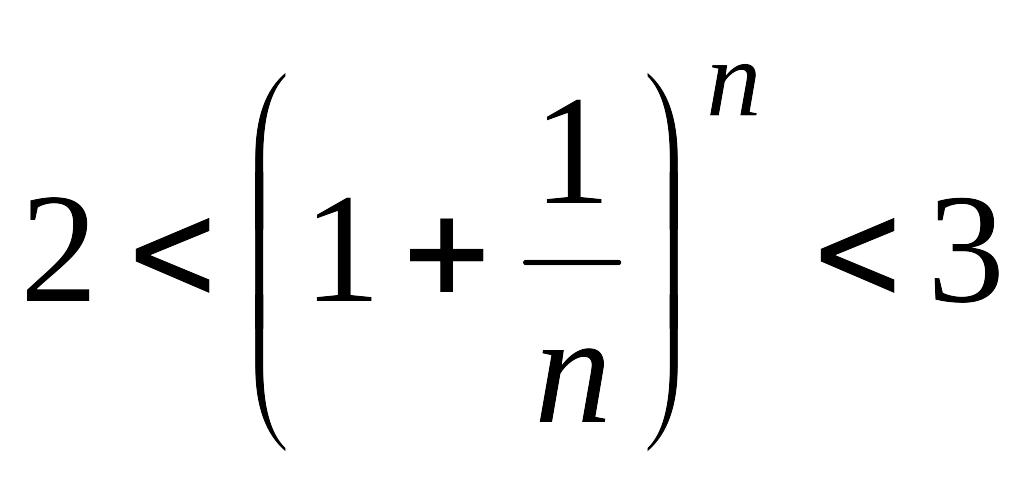Следовательно, на основании теоремы Вейерштрасса последователь­ность 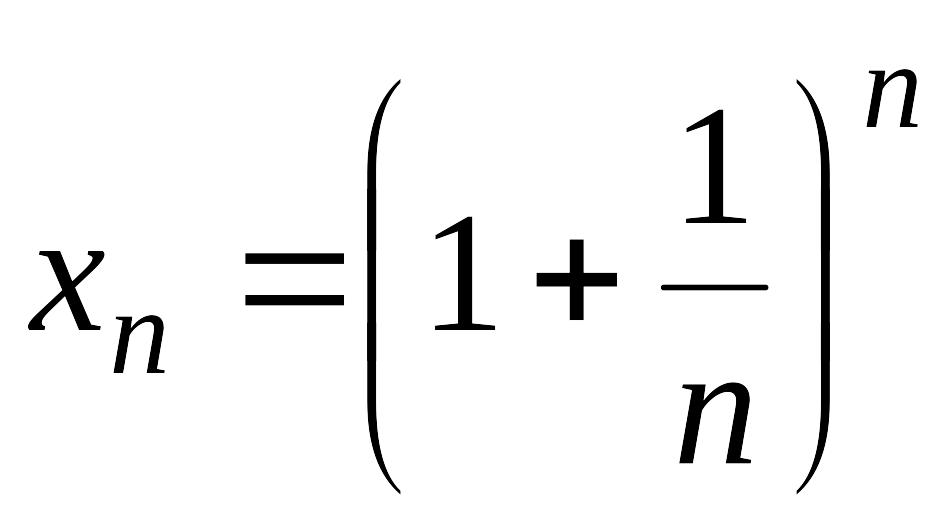, , имеет предел, обозначаемый обычно бук­вой :

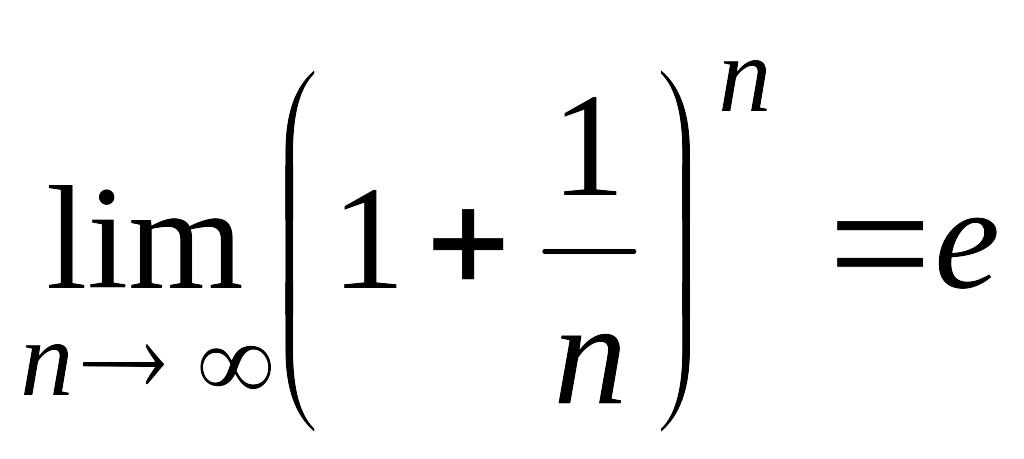. (15.6)

Число называют неперовым числом. Число иррациональное, его приближенное значение равно 2,72 ( = 2,718281828459045…). Число принято за основание натуральных логарифмов: логарифм по осно­ванию называется натуральным логарифмом и обозначается , т. е. .

Найдем связь между натуральным и десятичным логарифмами. По определению логарифма имеем . Прологарифмируем обе части равенства по основанию 10:

, т.е. .

Пользуясь десятичными логарифмами, находим . Значит, . Из этой формулы следует, что 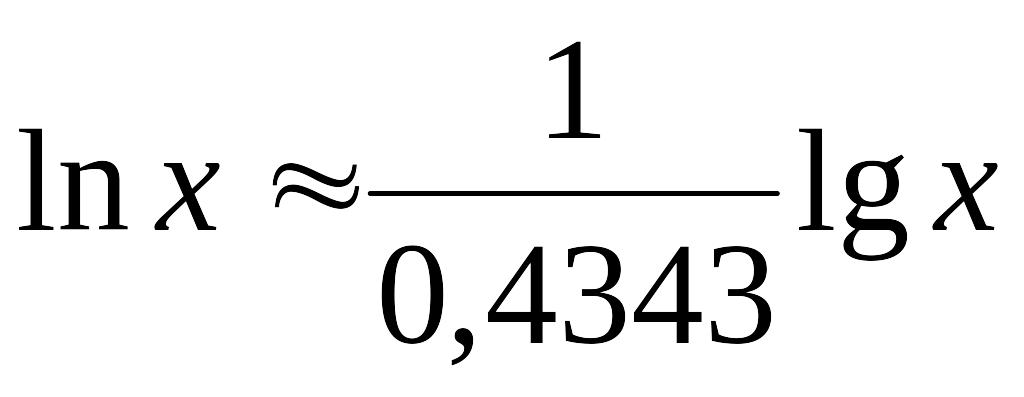, т.е. . Полученные формулы дают связь между натураль­ными и десятичными логарифмами.

§16. Предел функции

16.1. Предел функции в точке

Пусть функция определена в некоторой окрестности точки , кроме, быть может, самой точки .

Сформулируем два, эквивалентных между собой, определения пре­дела функции в точке.

Определение (на «языке последовательностей», или по Гейне). Число называется пределом функции в точ­ке (или при ), если для любой последовательности допусти­мых значений аргумента , ( ), сходящейся к (т.е. ), последовательность соответствующих значений функции , , сходится к числу (т.е. ).

В этом случае пишут или при . Геометрический смысл предела функции: означает, что для всех точек , достаточно близких к точке , соответствующие значения функции как угодно мало отличаются от числа .

Определение (на «языке - », или по Коши). Число на­зывается пределом функции в точке (или при ), если для любого положительного найдется такое положительное число , что для всех , удовлетворяющих неравенству , вы­полняется неравенство .

Записывают . Это определение коротко можно запи­сать так:

.

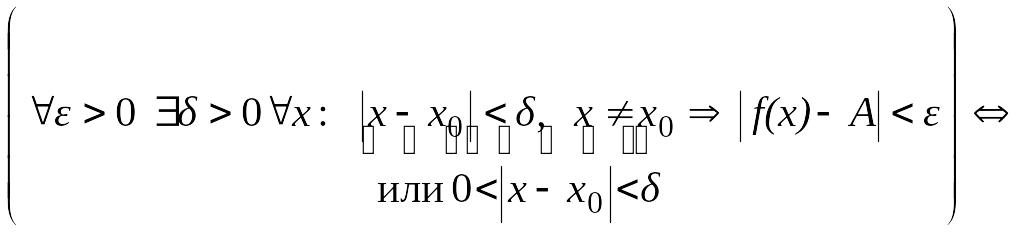
Геометрический смысл предела функции: , если для

любой -окрестности точки найдется такая ( -окрестность точки , что для всех из этой -окрестности соответствующие значения функции лежат в -окрестности точки . Иными словами, точки графика функции лежат внутри полосы шириной , ограни­ченной прямыми , (см. рис. 16.1). Очевидно, что величина зависит от выбора , поэтому пишут .

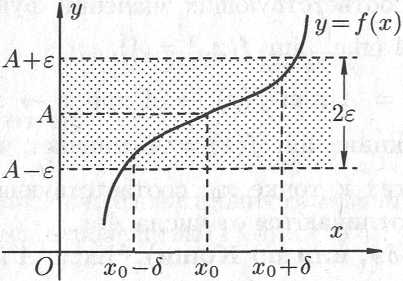
Рис. 16.1

Пример 16.1. Доказать, что .

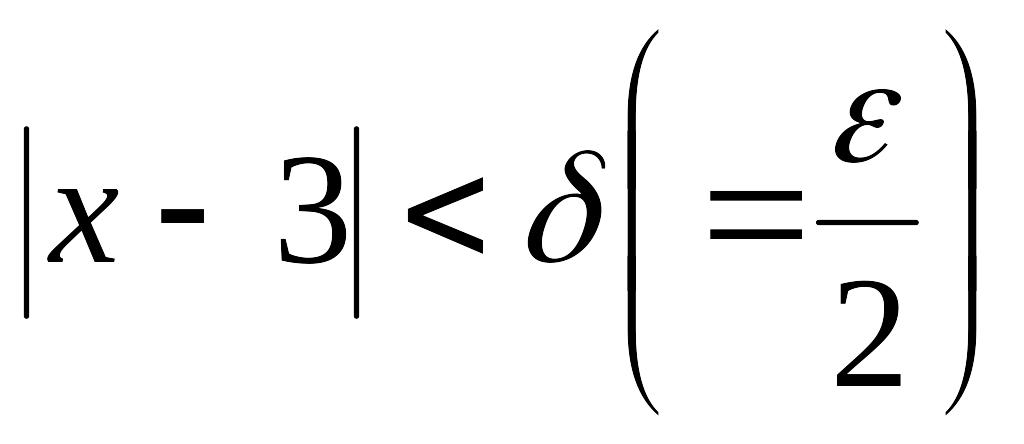Решение. Возьмем произвольное , найдем такое, что для всех , удовлетворяющих неравенству , выполняется неравенство , т.е. . Взяв , видим, что для всех , удовлетворяющих неравенству , выполняется неравенство . Следовательно, .

Пример 16.2. Доказать, что, если , то .

Решение. Для можно взять . Тогда при , имеем . Следовательно, .