14.5. Сложная функция

Пусть функция определена на множестве , а функция на множестве , причем для соответствующей значение . Тогда на множестве определена функция , которая называется сложной функцией от (или су­перпозицией заданных функций, или функцией от функции).

Переменную называют промежуточным аргументом сложной функции.

Например, функция : есть суперпозиция двух функций и . Сложная функция может иметь несколько проме­жуточных аргументов.

14.6. Основные элементарные функции и их графики

Основными элементарными функциями называют следующие функции.

1) Показательная функция , , . На рис. 14.7 пока­заны графики показательных функций, соответствующие различным основаниям степени.

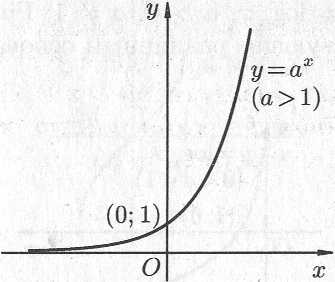
Рис. 14.7

2) Степенная функция , . Примеры графиков сте­пенных функций, соответствующих различным показателям степени, предоставлены на рис. 14.8.

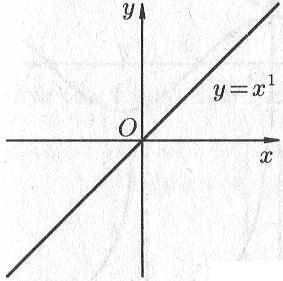
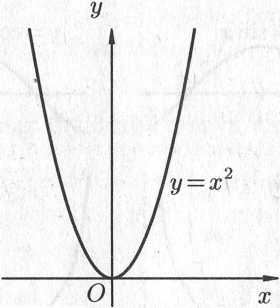
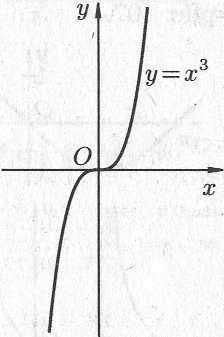
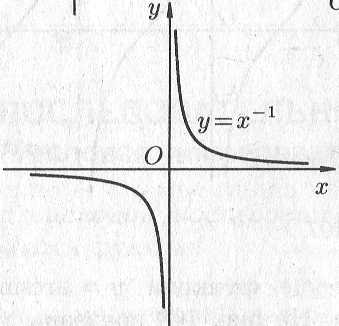
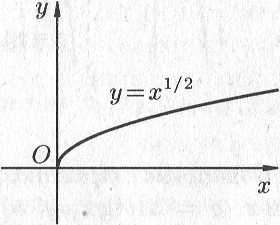
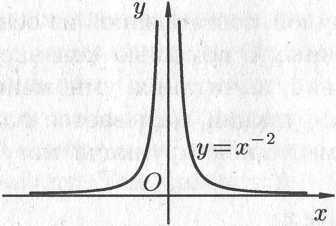
Рис. 14.8

3) Логарифмическая функция , , ; Графики логарифмических функций, соответствующие различным основаниям, показаны на рис. 14.9.

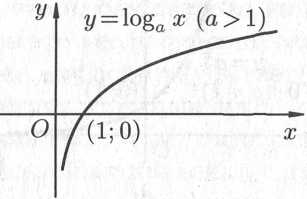
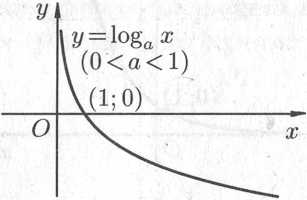
Рис. 14.9

4) Тригонометрические функции , , , ; Графики тригонометрических функций имеют вид, показанный на рис. 14.10.

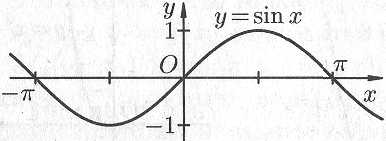
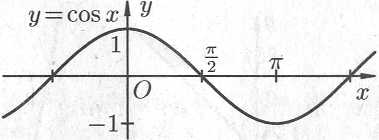
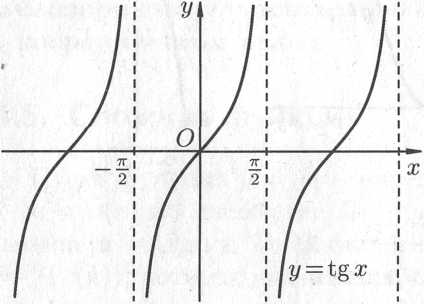
Рис. 14.10

5)Обратные тригонометрические функции , , , . На рис. 14.11 показаны графики обратных тригонометрических функций.

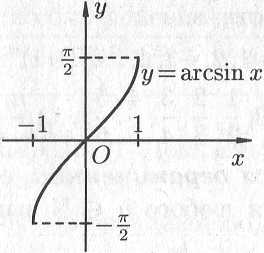
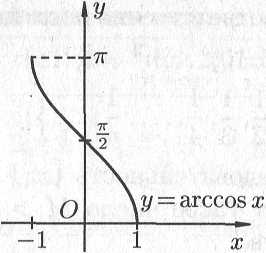
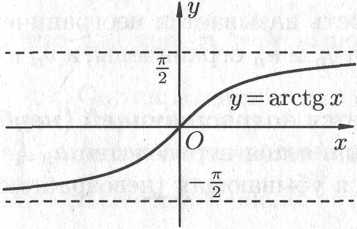
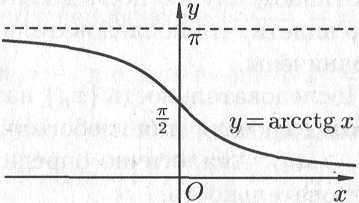
Рис. 14.11

Определение. Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного чи­сла арифметических операций (сложения, вычитания, умножения, де­ления) и операций взятия функции от функции, называется элементарной функцией. Примерами элементарных функций могут слу­жить функции

; ; .

Примерами неэлементарных функций могут служить функции

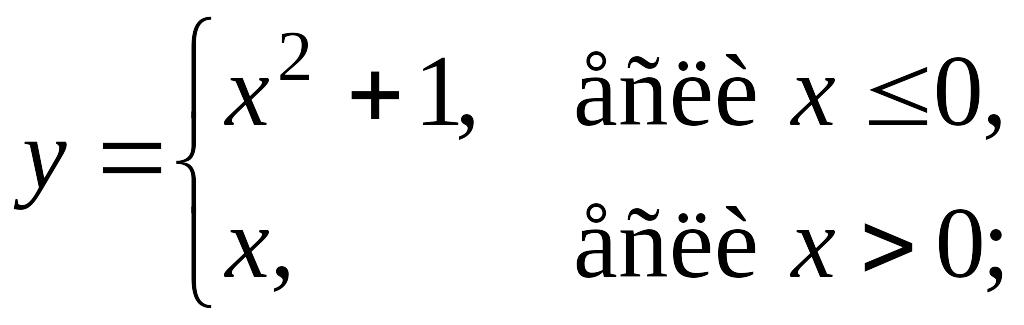
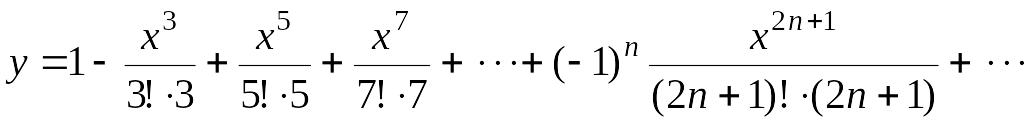
§15. Последовательности

15.1. Числовая последовательность

Определение. Под числовой последовательностью по­нимается функция

, (15.1)

заданная на множестве натуральных чисел.

Кратко последователь­ность обозначается в виде или , . Число называет­ся первым членом (элементом) последовательности, — вторым, …, — общим или -м членом последовательности.

Чаще всего последовательность задается формулой его общего чле­на. Формула (15.1) позволяет вычислить любой член последовательно­сти по номеру п, по ней можно сразу вычислить любой член последо­вательности. Так, равенства

, , , ,

задают соответственно последовательности

; ;

; .

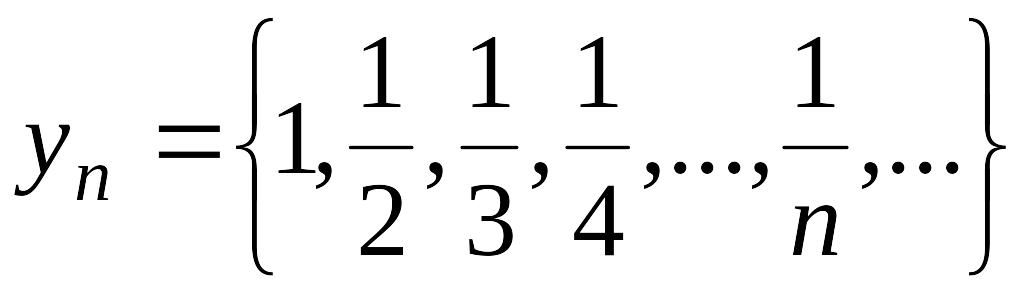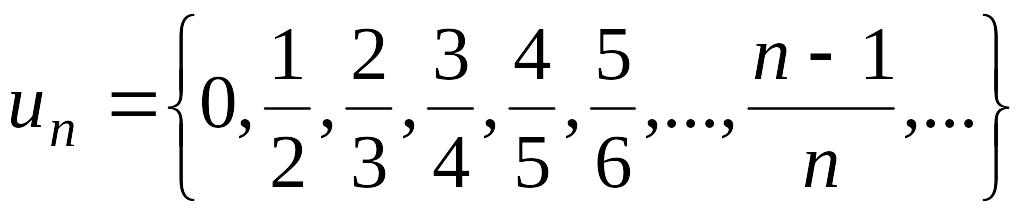Определение. Последовательность называется ограниченной, если суще­ствует такое число , что для любого выполняется неравенство

. В противном случае последовательность называется неограниченной.

Легко видеть, что последовательности и ограничены, a и — неограниченны.

Определение. Последовательность называется возрастающей (неубыва­ющей), если для любого выполняется неравенство ( ). Аналогично определяется убывающая (невозрастающая) последовательность.

Все эти последовательности называются монотонными после­довательностями. Последовательности , и монотонные, а — не монотонная.

Если все элементы последовательности равны одному и тому же числу с, то ее называют постоянной.

Другой способ задания числовых последовательностей — рекуррентный способ. В нем задается начальный элемент (первый член последовательности) и правило определения -го элемента по ( )-му: .

Таким образом, , и т. д. При таком способе за­дания последовательности для определения 100-го члена надо сначала посчитать все 99 предыдущих.