7.4. Некоторые приложения векторного произведения

Условие коллинеарности векторов.

Если , то (и наоборот), т. е.

Нахождение площади параллелограмма и треугольника.

Согласно определению векторного произведения векторов и , т. е. . И, значит, .

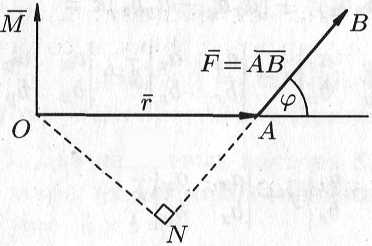
Определение момента силы относительно точки.

Пусть в точке приложена сила и пусть — некоторая точка пространства (см. рис. 7.5).

Из курса физики известно, что моментом силы относительно точки называется вектор , который проходит через точку и:

1. перпендикулярен плоскости, проходящей через точки , , ;

2. численно равен произведению силы на плечо

;

3. образует правую тройку с векторами и .

Стало быть, .

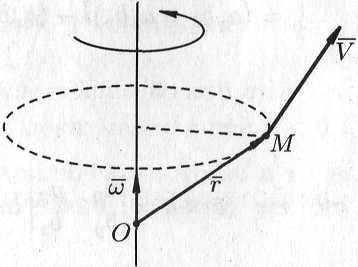
Нахождение линейной скорости вращения

Скорость точки твердого тела, вращающегося с угловой скоростью вокруг неподвижной оси, определяется формулой Эйлера , где , где — некоторая неподвижная точка оси (см. рис. 7.6).

Рис. 7.5

Рис. 7.6

§8. Смешанное произведение векторов

8.1. Определение смешанного произведения, его геометрический смысл

Рассмотрим произведение векторов , и , составленное следующим образом: . Здесь первые два вектора перемножаются вектор но, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Выясним геометрический смысл выражения . Построим параллелепипед, ребрами которого являются векторы , , и вектор .

Имеем: , , где — площадь парал­лелограмма, построенного на векторах и , для правой тройки векторов и для левой, где — высота параллелепипеда. Получаем: , т. е. , где — объем параллелепипеда, образованного векторами , и .

Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

8.2. Свойства смешанного произведения

Свойство 1.Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. .

Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.

Свойство 2.Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. .

Действительно, и . Знак в правой части этих равенств берем один и тот же, так как тройки векторов , , и , , — одной ориентации.

Следовательно, . Это позволяет записывать смешанное произведение векторов в виде без знаков векторного, скалярного умножения.

Свойство 3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. , , .

Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.

Свойство 4. Смешанное произведение ненулевых векторов , и равно нулю тогда и только тогда, когда они компланарны. Если , то , , — компланарны.

Допустим, что это не так. Можно было бы построить параллелепипед с объемом . Но так как , то получили бы, что . Это противоречит условию: .

Обратно, пусть векторы , , — компланарны. Тогда вектор будет перпендикулярен плоскости, в которой лежат векторы , , , и, следовательно, . Поэтому , т. е. .