§6. Скалярное произведение векторов и его свойства

6.1. Определение скалярного произведения

Определение. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается , (или ). Итак, по определению,

, (6.1)

где .

Формуле (6.1) можно придать иной вид. Так как , (см. рис. 6.1), a , то получаем:

, (6.2)

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

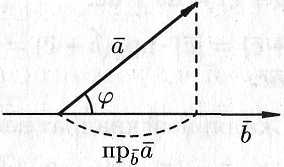
Рис. 6.1.

6.2. Свойства скалярного произведения

1. Скалярное произведение обладает переместительным свойством:

.

, а .

И так как , как произведение чисел и , то .

2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: .

.

3. Скалярное произведение обладает распределительным свойством:

.

.

4. Скалярный квадрат вектора равен квадрату его длины: .

.

В частности: .

Если вектор возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль , т. е. ( ).

Пример 6.1. Найти длину вектора , если , , .

Решение.

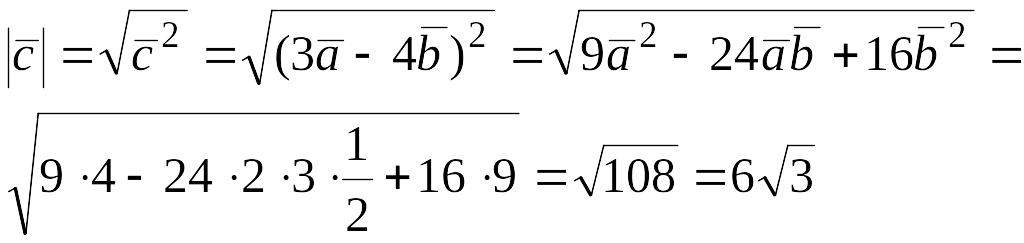
5. Если векторы и (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если , то . Справедливо и обратное утверждение: если и , то .

Так как , то . Следовательно, . Если же и , , то . Отсюда , т.e. .

В частности: .

6.3. Выражение скалярного произведения через координаты

Пусть заданы два вектора

и

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов , , :

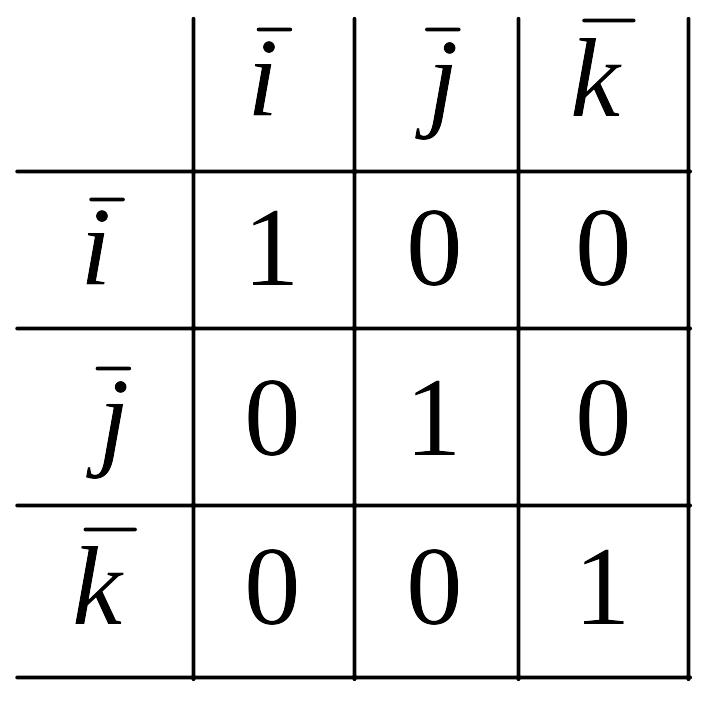
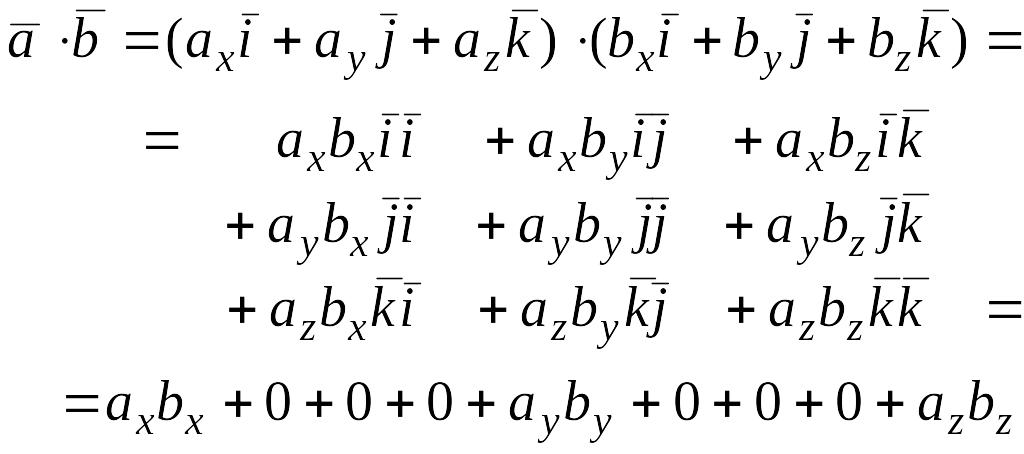
т. e.

.

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Пример 6.2. Доказать, что диагонали четырехугольника, заданного координатами вершин , , , , взаимно перпендикулярны.

Решение. Составим вектора и , лежащие на диагоналях данного четырехугольника. Имеем: и . Най­дем скалярное произведение этих векторов:

.

Отсюда следует, что . Диагонали четырехугольника взаимно перпендикулярны.

6.4. Некоторые приложения скалярного произведения

Угол между векторами.

Определение угла между ненулевыми векторами и :

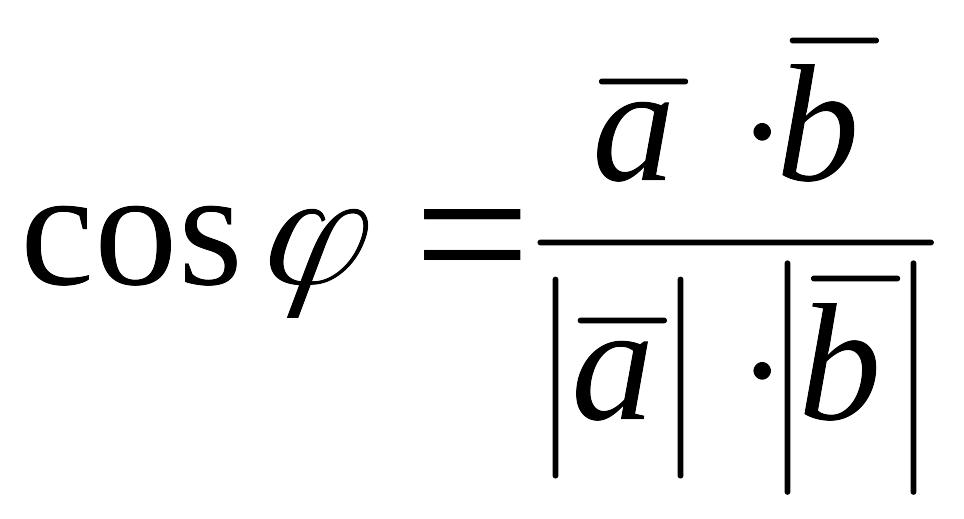, т.е. .

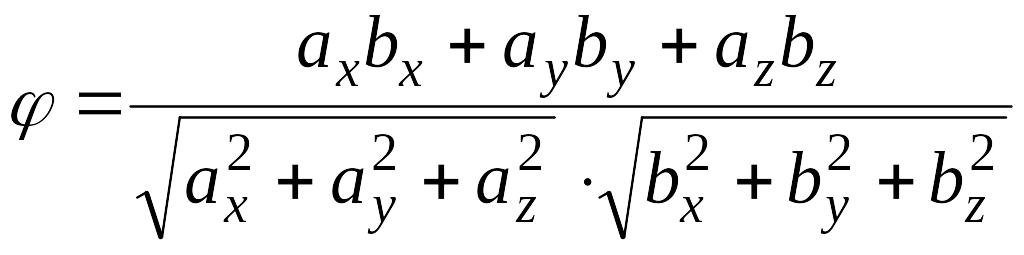Отсюда следует условие перпендикулярности ненулевых векторов и :

.

Проекция вектора на заданное направление.

Нахождение проекции вектора на направление, заданное векто­ром , может осуществляться по формуле

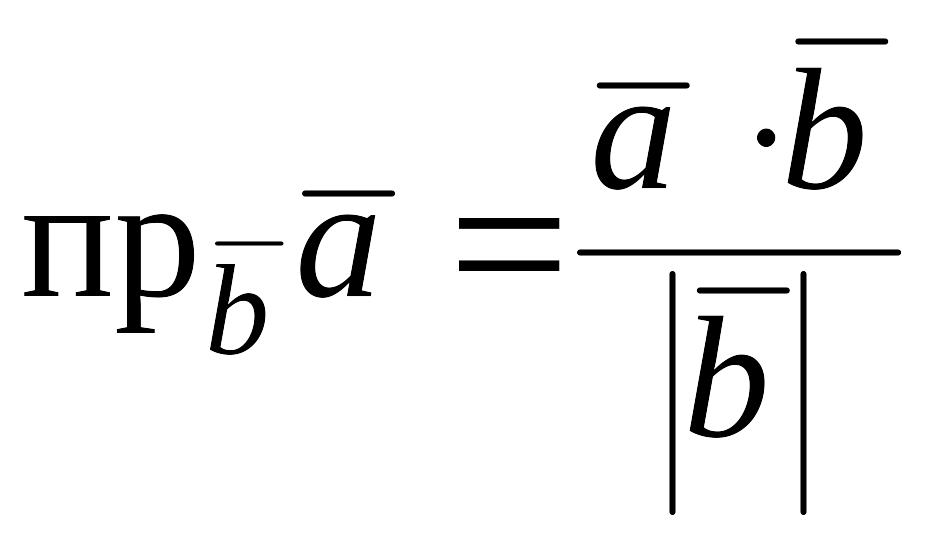
, т.е.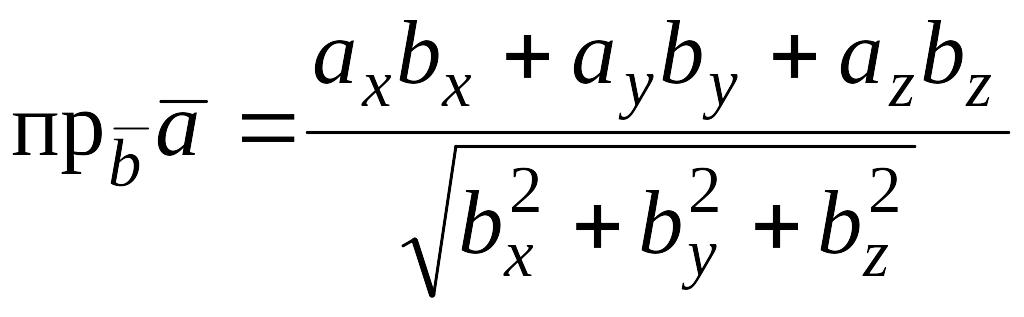

Работа постоянной силы.

Пусть материальная точка перемещается прямолинейно из поло­жения в положение под действием постоянной силы , образующей угол с перемещением (см. рис. 6.2).

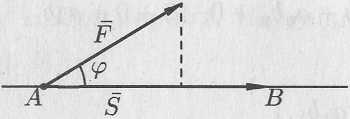
Рис. 6.2.

Из физики известно, что работа си­лы при перемещении равна

т.е. .

Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.

Пример 6.3. Вычислить работу, произведенную силой , если точка ее приложения перемещается прямолинейно из положения в положение . Под каким углом к направлена сила ?

Решение. Находим . Стало быть,

(ед. работы).

Угол между и находим по формуле

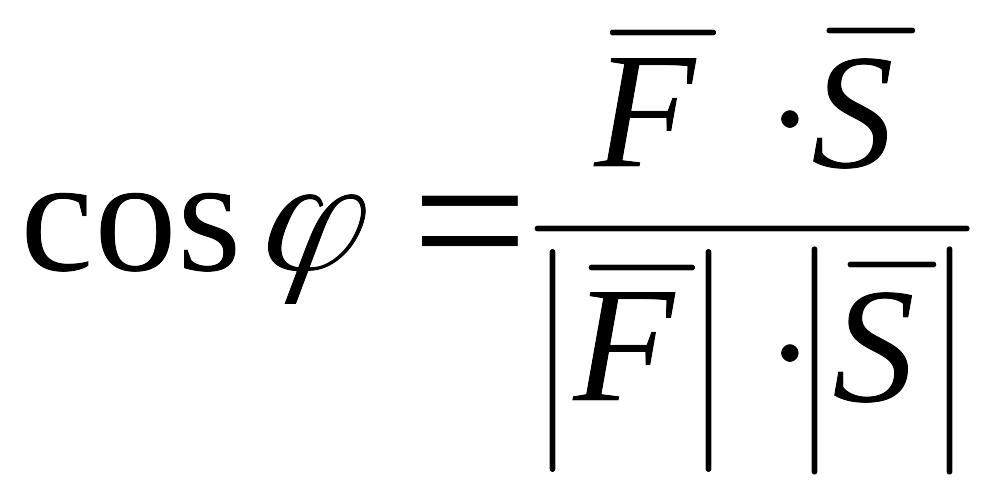, т. е.

, .