Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

Математика

Файл:

Решение тестовых заданий федерального интернет-экзамена по математике. Часть 1. Алгебра и геометрия. Колпачёв В.Н., Дементьева А.М

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

2.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Решение. Отрезок AB – это сторона квадрата. По формуле (3.1)

AB = (xB − xA )2 +(yB − yA )2 = (−2 −5)2 +(5 −6)2 = 50 .

Так как площадь S квадрата равна квадрату длины его стороны, то

S = ( 50 )2 = 50 ,

т.е. верен второй ответ.

Тестовое задание 3.11

Установите соответствие между элементами двух множеств ( ρ( A; B) –

расстояние между точками A и B )

1.ρ(A(4; 3); B(2; 4))

2.ρ(A(−2; 0); B(−2; 3))

3.ρ(A(7; −1); B(0; −1))

υ2 υ2	3
υ	3
υ222	3
υ	5
υ212	5
υ2 υ2	5
υ232	7
υ

Решение. Найдем ρ( A; B) = AB по формуле (3.1) для каждого из трех элементов множества расстояний.

ρ(A(4; 3); B (2; 4))=

(4 − 2)2 +(3 − 4)2

5 – соответствует третьему

ответу.

ρ(A(−2; 0); B (−2;

3 ))=

(−2 + 2)2 +(0 −

3 )2 = 3 – соответствует

второму ответу.

)

(

))

(

)

(

)

(

7; −

0; −

7 −0

2 +

= 7 – соответствует пятому

1 ; B

−1 +1

ответу.

Тестовое задание 3.12

Треугольник

ABC

вершинами

−3

A(1; −3),

B(α; 1), C (7; −1)

и основа-

2 +

нием

является

равнобедренным

при α равном…

101

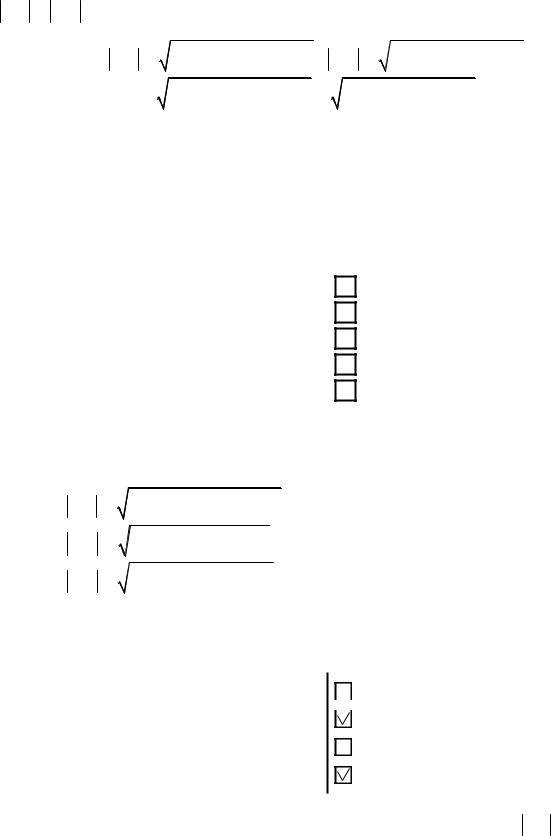
Решение. Если треугольник ABC равнобедренный и его основание – сторона AC , то боковые стороны – AB и BC и справедливо равенство AB = BC . Найдем длины боковых сторон по формуле (3.1) и приравняем их:

AB = (1 −α)2 +(−3 −1)2 , BC = (α −7)2 +(1 +1)2 ,

(1 −α)2 +(−3 −1)2 = (α −7)2 +(1 +1)2 .

Возводим обе части равенства в квадрат и приводим подобные: 1 − 2α +α2 +16 =α2 −14α + 49 + 4 .

Получим 12α = 36 , т.е. α = 3 – верен четвертый ответ.

Тестовое задание 3.13

Даны точки A(1; 0),		B(−2; −4) и	υ	5

C (1; −4). Установите		соответствие	υ212
			υ υ	3
между отрезком и его длиной.			232
			υ υ	4
1.	AB		222
			υ2 υ2	7
2.	AC
			υ2 υ2	6
3.	BC

Решение. Воспользуемся формулой (3.1).

1.AB = (−2 −1)2 +(−4 −0)2 = 5 – соответствует первому ответу.

2.AC = (1 −1)2 +(−4 −0)2 = 4 – соответствует третьему ответу.

3. BC = (1 + 2)2 +(−4 + 4)2 = 3 – соответствует второму ответу.

Тестовое задание 3.14

Если длина отрезка AB равна 5, то координаты начала и конца отрезка мо- гут быть равны соответственно…

A(0; 0) и B(5; 5)

A(−1; 3) и B(−1; −2)

A(0; 5) и B(5; 0)

A(−1; 0), B(2; 4)

Решение. Снова воспользуемся формулой (3.1). Найдем AB в каждом

102

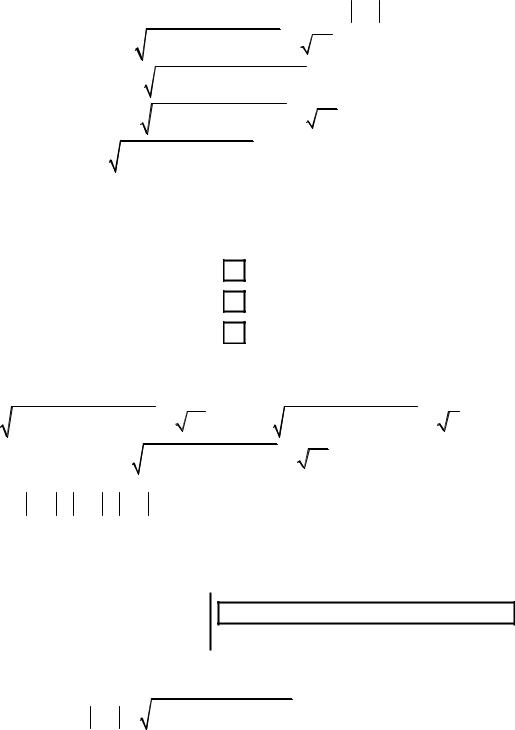
предлагаемом варианте ответов и выберем те ответы, где AB = 5.

В первом ответе –

(5 −0)2 +(5 −0)2

50 ≠ 5 .

Во втором ответе –

(−1 +1)2 +(−2 −3)2

= 5.

В третьем ответе –

(5 −0)2 +(0 −5)2

50 ≠ 5

и в четвертом ответе

= (2 +1)2 +(4 −0)2

= 5 .

Верны второй и четвертый ответы.

Тестовое задание 3.15

Расположите

по возрастанию

длины

сторон треугольника

ABC , где

υ232

A(5; 3), B(0; −3) и C (3; 4).

υ222

υ212

Решение. Найдем длины сторон треугольник

ABC по формуле (3.1):

(0 −5)2 +(−3 −3)2 = 61 ,

(3 −5)2 +(4 −3)2 = 5 ,

= (3 −0)2 +(4 +3)2 = 58 .

Очевидно, AC < BC < AB , что соответствует нумерации 1, 2, 3 соответственно.

Тестовое задание 3.16

Расстояние между точками A(3; 1) и 5 B(0; −3) равно …

Решение. По формуле (3.1):

AB = (0 −3)2 +(−3 −1)2 = 5 .

Ответ: 5.

3.2.2.Прямая на плоскости

Втестовых заданиях 3.17 – 3.23 используется понятие углового коэффициента прямой (определение 3.1) и уравнение прямой с угловым коэффициентом (уравнение 3.6).

103

Тестовое задание 3.17

Установите соответствие между урав-								3
нением прямой и её угловым коэффи-							υ2 υ2	3
нением прямой и её угловым коэффи-							υ2 υ2	4
циентом								4	3
циентом							υ212
1. 3x + 4 y −3 = 0							υ212	−
							υ		4
2. 2 y +3 = 0							υ222		4
2. 2 y +3 = 0							υ222	0
3. 3x −5 = 0							υ
3. 3x −5 = 0							υ2 υ2	3
							υ2 υ2	3
							υ232	не существует
							υ
Решение. Приведем данные уравнения прямых к виду (3.6), для чего вы-
разим из уравнения переменную у.
1. y =	3 −3x	или y = −	3	x +	3	; коэффициент при х в правой части уравне-
1. y =		или y = −		x +	4	; коэффициент при х в правой части уравне-
4		4			4

ния – это угловой коэффициент прямой, т.е k = − 34 – соответствует второму от-

вету.

2.y = − 32 , т.е. y = 0 x − 32 , т.е. k = 0 – соответствует третьему ответу.

3.Уравнение не содержит у, т.е. не приводится к виду (3.6). Отсюда следует, что прямая не имеет углового коэффициента – соответствует пятому ответу.

Тестовое задание 3.18

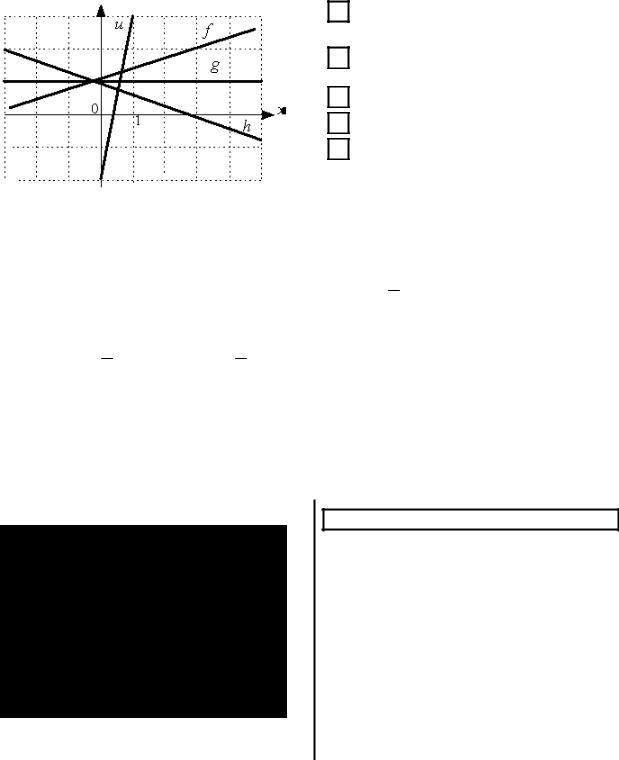
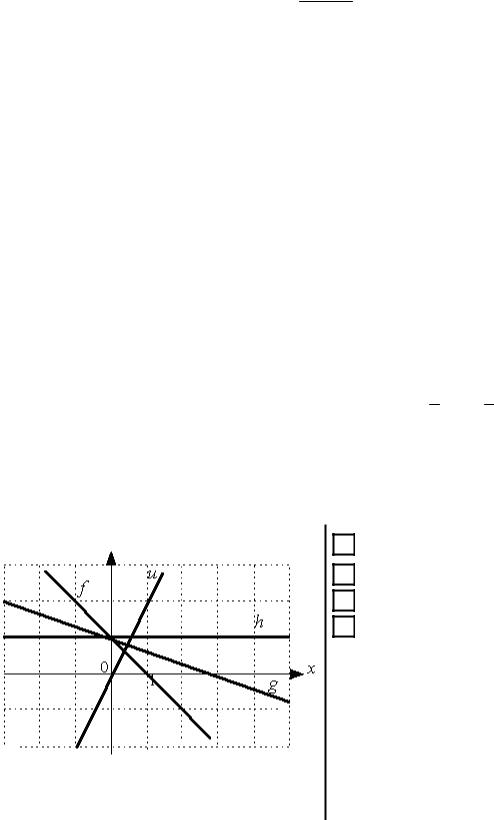
Даны графики прямых f , g, h, u :	5

Тогда сумма их угловых коэффициентов равна…

Решение. Чтобы определить графически угловой коэффициент прямой, нужно увидеть угол наклона прямой к положительному направлению оси Ox , а затем найти тангенс этого угла. Для этого на прямой берутся две точки (x1; y1 )

104

и (x2 ; y2 ) (если возможно, то с целыми координатами), и тогда искомый тангенс угла ищется по формуле

k = y2 − y1 x2 − x1

(фактически определяют отношение противолежащего катета к прилежащему). На прямой u видны точки (1;3) и (0; −2), поэтому

−2 −3

= 5 .

0 −1

На прямой f

видны точки (3;2) и (0;1), поэтому

k f

1 − 2

0 −3

Прямая

g имеет уравнение

y =1,

т.е.

kg = 0 . Прямая h проходит через

точки (3;0) и (0;1), поэтому

1 −0

= −

0 −3

Сложим найденные угловые коэффициенты: 5 + 13 + 0 − 13 = 5 .

Ответ: 5.

Тестовое задание 3.19

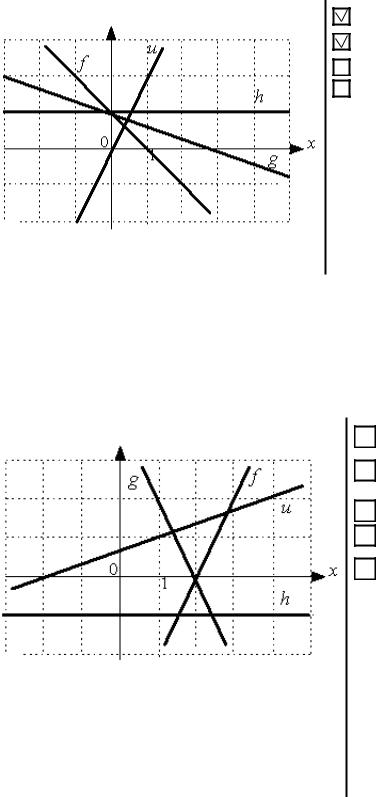
Даны графики прямых f , g, h, u :	f
υ242	f
υ
υ	u
υ212	u
υ	h
υ222	h
υ23υ2	g

Укажите последовательность этих прямых в порядке убывания их угловых коэффициентов.

105

Решение. Вычислим угловые коэффициенты прямых так же, как и в задании 3.18. На прямой u видны точки (1;2) и (0;0), поэтому

ku = 00−−12 = 2 .

Прямая h параллельна оси Ox , поэтому kh = 0 . Прямая g проходит через точки (0;1) и (3;0), поэтому

kg	=		0 −1		= −	1	.
			3 −0
					3
Наконец, прямая f проходит через точки (−1;2) и (1;0), поэтому
k f	=			0 − 2	= −1.
			1 +1

Сравниваем значения: −1 < −		1	< 0 < 2, т.е. k f < kg < kh < ku или, наоборот,
	3

ku > kh > kg > k f , что соответствует нумерации 1, 2, 3, 4.

Тестовое задание 3.20

Даны графики прямых f , g, h, u :	f

h u

Тогда положительный угловой коэффициент имеют прямые…

Решение. Угловой коэффициент прямой положителен, если угол наклона прямой к положительному направлению оси Ox острый. Видно, что под острым углом наклонены к Ox прямая u и прямая f (верны первый и четвертый

ответы).

106

Тестовое задание 3.21

Даны графики прямых f , g, h, u :	f

h u

Тогда отрицательный угловой коэффициент имеют прямые…

Решение. Угловой коэффициент прямой отрицателен, если угол наклона прямой к положительному направлению оси Ox тупой. Видно, что под тупым углом наклонены к Ox прямая f и прямая g (верны первый и второй ответы).

Тестовое задание 3.22

Даны графики прямых f , g, h, u :	υ232	0
	υ
	υ2 υ2	−	1
	υ2 υ2	−	3
	υ222	−2
	υ	2
	υ212	2
	υ
	υ	1
	υ
	υ242	3
		3

Установите соответствие между прямыми

1.f

2.g

3.h

4.u

и значениями их угловых коэффициентов.

Решение. В этом задании снова нужно вычислить угловые	коэффициен-
ты. Прямая f проходит через точки (2;0) и (3;2), поэтому k f =	2 −0	= 2 , что
	3 − 2

107

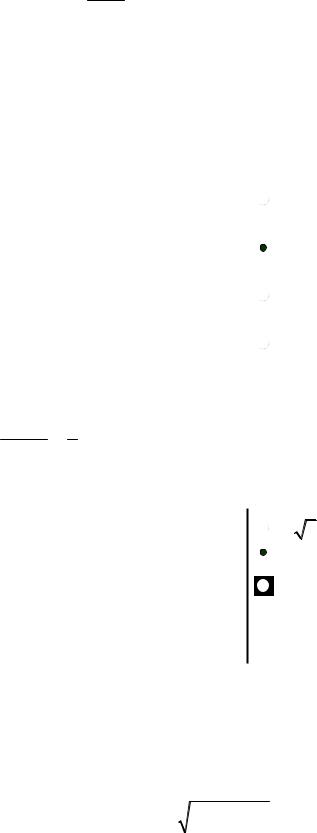
соответствует четвертому ответу. Прямая g проходит через точки (1;2) и

(2;0), поэтому kg = 02−−12 = −2 , что соответствует третьему ответу. Прямая h

параллельна оси Ox , поэтому kh = 0 , что соответствует первому ответу. И, на-

конец, на прямой u видны точки (−2;0)	и (1;1), т.е. ku =				1 −0	=	1	, что соответ-
конец, на прямой u видны точки (−2;0)	и (1;1), т.е. ku =			1 + 2		=	3	, что соответ-
ствует пятому ответу.
Тестовое задание 3.23
Прямая проходит через точки O(0; 0),		−	5


B(25; 15). Тогда ее угловой коэффи-			3
B(25; 15). Тогда ее угловой коэффи-			3
циент равен…		3
циент равен…		3
		5	3
		5
		−
		5	5
			5

		3
		3

Решение. Две точки на прямой известны, поэтому (см. тестовое задание

3.18) kg = 1525 −−00 = 53 , что соответствует второму ответу.

Тестовое задание 3.24
Расстояние от точки A(1; 2)	до пря-	2	2
Расстояние от точки A(1; 2)	до пря-
мой 3x = 4 y равно…
мой 3x = 4 y равно…		1
		1
		2
		2

2 15

Решение. Воспользуемся формулой (3.17) (расстояние от точки до прямой), для чего приведем уравнение данной прямой к общему: 3x − 4 y = 0 . Те-

перь по формуле (3.17), где (x0 ; y0 ) – это точка A(1; 2), имеем

d =	3 1 −4 2	=	5	=1,


			5
	32 +(−4)2

что соответствует второму ответу.

108

Тестовое задание 3.25
Ордината точки	пересечения прямой	1
Ордината точки	пересечения прямой
28x +14 y −28 = 0	с осью Oy равна…
28x +14 y −28 = 0	с осью Oy равна…	14
		14
		2
		−2

Решение. Точки, лежащие на оси Oy , имеют абсциссы, равные нулю, поэтому подставим в уравнение данной прямой x = 0 , получим y = 2 , что соответствует третьему ответу.

Тестовое задание 3.26
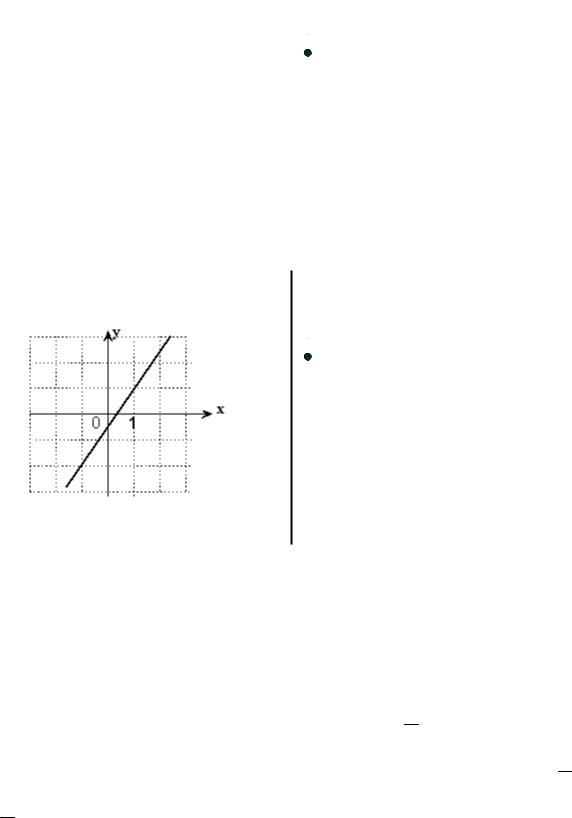
График прямой линии, заданной урав-		BC = 0
График прямой линии, заданной урав-
нением Ax + By +C = 0	, имеет вид
нением Ax + By +C = 0	, имеет вид	BC < 0
		BC < 0
		AB > 0
		AB < 0

Правильным утверждением является…

Решение. В этом задании дано общее уравнение прямой (3.9). Данная прямая не перпендикулярна оси Ox ( B ≠ 0 ), поэтому ее уравнение можно привести к виду (3.6), выразив у через х. Получим уравнение

y = −	A	x −	C	.	(3.54)

	B B

В этом уравнении угловой коэффициент прямой k = − BA . Так как угол наклона прямой к положительному направлению оси Ox острый, то k > 0 , т.е. − BA > 0

или BA < 0 , а значит, A и B разных знаков, т.е. четвертый ответ верный. Пря109

мая не проходит через начало координат, поэтому C ≠ 0 , значит, первый ответ неверен. Из уравнения (3.54) видна ордината точки пересечения прямой с Oy

(свободный член), равная −CB . По чертежу видно, что эта ордината отрица-

тельна, т.е. −CB < 0 , откуда CB > 0 , а значит, C и B одного знака. Поэтому вто-

рой ответ неверен. Третий ответ неверен, так как противоречит верному ответу.

Тестовое задание 3.27

Укажите правильное соответствие между уравнениями и типами уравнений прямой на плоскости

1.y +6 = −2(x +3)

2.−x3 + −y5 =1

3.2x −7 y +9 = 0

υ2 υ2 уравнение прямой с угловым коэффициентом

υ2 υ2 уравнение прямой, параллельной оси абсцисс

υ22υ2 уравнение прямой в отрезках на осях

υ21υ2 уравнение прямой, проходящей через заданную точку в заданном направлении

υ23υ2 общее уравнение прямой

Решение. Очевидно, первое уравнение вида (3.7) – четвертый ответ. Второе уравнение вида (3.11) – третий ответ. Третье уравнение вида (3.9) – пятый ответ.

Тестовое задание 3.28
Параметрическими уравнениями пря-	x		=t +12,


мой на плоскости являются уравне-

ния…	y		= −8


		y = x −19
		x + 4 y −7 = 0
		x +1		=	y −3

	9		4

Решение. Для решения вспомним формулу (3.13). Ей соответствует первый ответ.

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете Математика