Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1852

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

2.48 Mб

Скачать

☆

1 / 161 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

А. П. Бырдин, А. А. Сидоренко, О. А. Соколова

РУКОВОДСТВО К ПРОВЕДЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО КУРСУ «МАТЕМАТИКА» ВО ВТОРОМ СЕМЕСТРЕ

Учебное пособие

divFdV FndS

V S

Воронеж 2018

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования «Воронежский государственный технический университет»

А. П. Бырдин, А. А. Сидоренко, О. А. Соколова

РУКОВОДСТВО К ПРОВЕДЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО КУРСУ «МАТЕМАТИКА» ВО ВТОРОМ СЕМЕСТРЕ

Утверждено учебно-методическим советом университета в качестве учебного пособия

Воронеж 2018

УДК 517.2(075.8) ББК 22.1я7

Б95

Рецензенты:

кафедра математического моделирования Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. В. А. Костин);

канд. физ.-мат. наук, доц. В. И. Кузнецова

Бырдин, А. П.

Руководство к проведению практических занятий Б95 по курсу «Математика» во втором семестре: учеб. пособие / А. П. Бырдин, А. А. Сидоренко, О. А. Соколова; ФГБОУ ВО «Воронежский государственный технический

университет». - Воронеж: Изд-во ВГТУ, 2018. - 152 с.

ISBN 978-5-7731-0664-7

Учебное пособие содержит теоретический материал, необходимый для решения прикладных задач, который иллюстрируется большим количеством примеров. Имеются задачи для самостоятельного решения и типовых расчетов.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего образования по направлению 21.03.01 «Нефтегазовое дело» (профиль «Эксплуатация и обслуживание объектов транспорта и хранения нефти, газа и продуктов переработки»), дисциплине «Математика».

Предназначено для студентов первого курса.

Ил. 9. Библиогр.: 6 назв.

УДК 517.2(075.8) ББК 22.1я7

ISBN 978-5-7731-0664-7 © Бырдин А. П., Сидоренко А. А.,

Соколова О. А., 2018 © ФГБОУ ВО «Воронежский

государственный технический университет», 2018

ВВЕДЕНИЕ

При написании учебного пособия авторы использовали опыт проведения практических занятий по курсу «Математика» для различных специальностей Воронежского государственного технического университета. В частности, данное пособие предназначено для студентов очной формы обучения направления подготовки бакалавров «Нефтегазовое дело» и написано в соответствии с рабочей программой этой специальности, но может быть использовано и для студентов других специальностей.

В учебном пособии представлен материал, который изучается во втором семестре. Цель работы – помочь студентам усвоить и закрепить основные положения линейной алгебры, аналитической геометрии и начала анализа.

При написании учебного пособия авторы стремились изложить материал по возможности полно, строго и доступно. Представленная работа направлена на совершенствование учебного процесса и способствует целенаправленному использованию знаний математики. Учебное пособие поможет студентам лучше усвоить теоретический материал, даст возможность самостоятельно научиться решать типовые задачи, подготовиться к экзамену или зачету.

По каждому разделу приведены примеры решения задач, а также многочисленные задачи для контроля усвоения материала. Ко всем рекомендуемым для самостоятельного решения задачам приведены ответы. Поэтому представленное учебное пособие полезно использовать преподавателями для проведения практических занятий.

Все приведенные в работе иллюстрации являются авторскими.

1. КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ

Литература: [1, гл. 7, §§ 1 5].

Комплексным числом называется выражение вида

z a ib ,

(1.1)

где a и b - действительные числа, i - мнимая единица, удов-

летворяющая условию i 2 1. Числа a и b называются действительной и мнимой частями комплексного числа, соответственно a Re z , b Im z . Выражение (1.1) называется алгебраической формой записи комплексного числа.

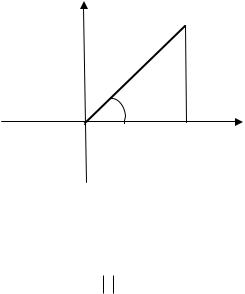
Геометрически каждому числу z a ib на координатной плоскости xOy соответствует точка M (x; y) (рис. 1). В этом случае плоскость xOy называется плоскостью комплексного переменного z .

M (x; y)
	z	y
	z	y
	arg z
0		x
x

Рис. 1

Полярные координаты точки M (x; y) называются соответственно модулем и аргументом комплексного числа z . Для них вводятся обозначения: z , Arg z . Те из значений полярного угла, которые удовлетворяют неравенству

, называются главными значениями угла и обозначаются arg z .

Соотношения между модулем и аргументом комплексного числа z и его действительной и мнимой частью устанавливаются формулами

a cos , b sin .

(1.2)

Отсюда

cos

, sin

(1.3)

a2 b2

Аргумент z

определяется неоднозначно по формуле

			b
arctg				,
arctg			a	,
			a
			b
arctg			b	,
arctg				,
			a
			b
			b
arg z arctg				,
arg z arctg			a	,
			a
		,
	2
	2

	,

	2

a 0,
a 0,	b 0,
a 0,	b 0,	(1.4)
a 0,	b 0,
a 0,	b 0.

Заменяя a и b в выражении (1.1) их выражениями через

и , получим тригонометрическую форму записи			ком-
плексного числа
z (cos i sin ) .			(1.5)
Пусть даны два комплексных числа	z1 a1 ib1		и
z2 a2 ib2 . Эти числа являются равными,	если у них равны
действительные и мнимые части, т.е. a1 a2 ,		b1 b2 .	Для

чисел, заданных в тригонометрической форме, равенство имеет место, если модули этих чисел равны, а аргументы отличаются на целое кратное 2 , т.е.

z1 z2 ,

и Arg z1 Arg z2

2k .

Два комплексных числа z a ib

и z a ib называ-

ются сопряженными. Для

сопряженных комплексных чисел

выполняются соотношения

arg z1 arg z2.

Пусть даны

два комплексных

числа

z1 a1 ib1 и

z2 a2 ib2 . Действия над этими комплексными числами

определяются по правилам.
Сложение.	z1 z2 (a1 a2 ) i(b1 b2 ) .
Вычитание.	z1 z2	(a1 a2 ) i(b1 b2 ) . При этом

полезно знать, что модуль разности двух комплексных чисел z1 и z2 равен расстоянию между точками, являющимися их изображениями на плоскости z : z1 z2 d(z1, z2 ) .

Умножение. z1 z2 (a1 a2 b1 b2 ) i(a1 b2 a2 b1) .

Если z1 1(cos1 i sin 1) , z2 2 (cos2 i sin 2 ) , то z1 z2 1 2 [cos( 1 2 ) i sin( 1 2 ) .

Таким образом, модуль произведения равен произведению модулей сомножителей, а аргумент произведения – сумме аргументов сомножителей.

Деление. Для нахождения частного двух комплексных чисел, заданных в алгебраической форме, следует делимое и делитель умножить на число, сопряженное с делителем:

a1 ib1

(a1 ib1) (a2 ib2 )

a2 ib2

(a2 ib2 ) (a2 ib2 )

(a1a2 b1b2 ) i (a2b1 a1b2 )

a1a2 b1b2

a2b1 a1b2

a 2

Если z1 1(cos 1 i sin 1) ,				z2 2 (cos 2			i sin 2 ) , то
	z1	1	[cos(		2	) i sin(		2	) .

	z2	2	1			1

					6

Таким образом, модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности

аргументов делимого и делителя.

Возведение в степень. Если z (cos i sin ) , то z n n (cos n i sin n )

(здесь n может быть как целым положительным, так и целым

отрицательным числом).

Извлечение корня. Если z (cos i sin ) и n целое положительное число, то корень n -й степени из комплексного

числа z имеет n различных значений,

которые находятся по

формуле

2 k

i sin

2 k

n z n cos

где k 0,1,2,..., n 1.

Пример.

Найти

z1 z2

если

z 2 3i ,

3 5i ,

z3 1 4i .

Решение.

Сначала вычислим произведение z1 z2

z1 z2 (2 3i) (3 5i) 6 10i 9i 15 21 i .

Далее находим

z1 z2

(21 i) (1 4i)

21 84i i 4

(1 4i) (1 4i)

1 16

17 17

Пример.

Представить

тригонометрической

форме

комплексное число z 1 i

Решение.

Находим

1 3 2 ,

arg z arctg

arctg 3

. Следовательно,

i sin

2 cos

		Пример.											Даны два									комплексных																	числа			z1 1 i					и

z2				3 i . Записать их в тригонометрической форме. Найти в
тригонометрической форме:
1) z z								2)					z1	; 3) z5 ; 4) 3																	.
					2	;							z1																z
						;																							z
	1											z2							1											1
																			1

		Решение. Запишем в тригонометрической форме эти
комплексные числа
														1 arctg1
1			1 1																														z1										i sin
1			1 1								2 ,														4			и					z1							2 cos		4	i sin		4	,
																									4																	4			4
																					1
2				3 1 2 , 2											arctg						1
																										6				и					z1			2 cos				6	i sin		6	.

																						3
																						3
		Далее находим:
																																									5			5
																																									5			5
1) z1 z2								2 2 cos											i sin															2					2 cos				i sin			.
1) z1 z2								2 2 cos										6	i sin											6				2					2 cos		12		i sin	12		.
														4				6							4					6											12			12
	z
						2
						2
2)	1								cos										i sin																			2 cos					i sin				.
2)									cos										i sin																			2 cos					i sin				.
	z2					2							4				6							4																	12
	z2					2							4				6							4						6											12				12

3)	z5						25 cos 5 i sin 5 .
	1
															2k														2k
					6									4	2k												4		2k
4)	3 z							2		cos				4						i sin							4									.
4)	3 z							2		cos										i sin																.
	1															3														3


Если k 0 , то														6

												0					2 cos									i sin										;
												0					2 cos					12				i sin										;
																						12										12
														6								3											3
																						3											3
		k 1 , то														2 cos										i sin											;
		k 1 , то														2 cos										i sin											;
											1												4										4
																							4										4
																							17											17
		k 2 , то											0 6 2										17					i sin						17
																			cos																					.
																			cos				12																	.
																							12													12
																										8

2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Литература: [1, гл. 10, §§ 1 10].

2.1. Первообразная. Неопределённый интеграл

Определение. Функция F(x) называется первообразной функцией для функции ƒ(х) на интервале (a, b), если F(x) диф-

ференцируема на (a, b) и F/(x)=ƒ(х) или dF(x)=ƒ(x)dx для всех x (a, b) .

Простейшие примеры:


	x	3			1		1
1. f x x2; F x	x				1	x3	1	3x2
			,	так как					;
			,	так как					;
	3				3		3
2. f x cos x; F x sin x,					так как	sinx cos x .

Если для ƒ(х) существует первообразная F(x), то существует и бесчисленное множество первообразных, отличающихся друг от друга на константу. Например, для ƒ(х) = х2 первообразными будут функции:

1	x	3	;	1	x	3	1;	1	x	3	10	и т.д.
3				3				3

Определение. Если функция F(x) является первообразной для ƒ(х), то выражение F x С называется неопределён-

ным интегралом функции ƒ(х) и обозначается символом

f x dx F x С

Операцию нахождения неопределённого интеграла (первообразной) называют интегрированием функции ƒ(х). Функция, имеющая первообразную, называется интегрируемой. Для функции, непрерывной на (a, b) существует первообразная на (a, b), т.е. она интегрируема. Интегрирование есть операция обратная дифференцированию.

Из определения неопределенного интеграла следует:

1) производная от неопределённого интеграла равна подынтегральной функции (применяется для проверки):

1 / 161 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20222.46 Mб7Учебное пособие 1848.pdf
#
30.04.20222.47 Mб1Учебное пособие 1849.pdf
#
30.04.2022316.27 Кб2Учебное пособие 185.pdf
#
30.04.20222.47 Mб9Учебное пособие 1850.pdf
#
30.04.20222.48 Mб1Учебное пособие 1851.pdf
#
30.04.20222.48 Mб3Учебное пособие 1852.pdf
#
30.04.20222.49 Mб9Учебное пособие 1853.pdf
#
30.04.20222.49 Mб4Учебное пособие 1854.pdf
#
30.04.20222.49 Mб3Учебное пособие 1855.pdf
#
30.04.20222.5 Mб4Учебное пособие 1856.pdf
#
30.04.20222.51 Mб6Учебное пособие 1857.pdf