3.4. Метод Гаусса Суть метода Гаусса в том, чтобы с помощью элементарных преобразований матриц получить матрицу вида:

(3.10)

1. Рассмотрим элемент , если , то умножим его на( ), ( ) и т.д. и прибавляем его ко 2-й, 3-й и т.д. строкам. Если же , то меняем местами строки или столбцы. Этого можно достичь всегда, если только матрица не имеет вид :

- вид матрицы . (3.11)

В результате

.

1. Рассмотрим матрицу 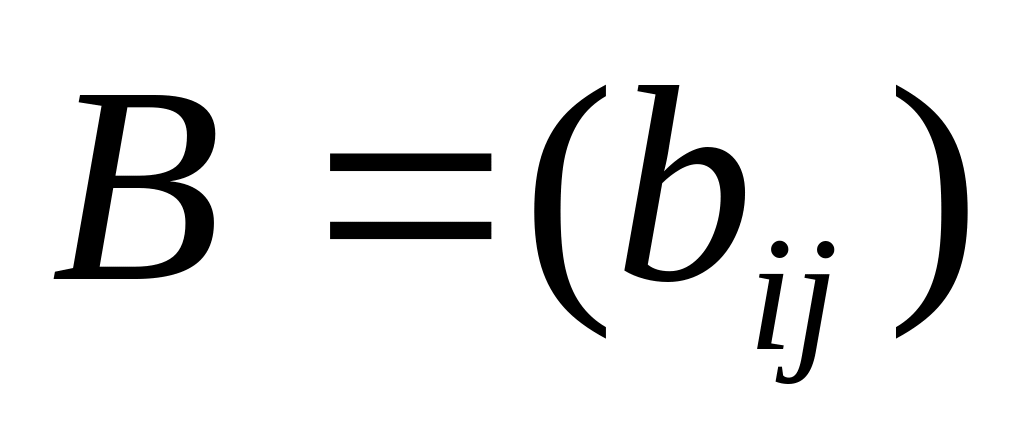, делаем те же преобразования.

П олучаем

4. Рассмотрим матрицу С. Произведем те же преобразования. После этого получим матрицу вида (3.10).

Находим множество решений системы (3.1). Исследуем (решаем) систему, соответствующую матрице (3.10). Итак, матрица (3.10) соответствует системе линейных уравнений вида:

(3.12)

где - это неизвестные переставленные определенным образом. Их перестановка определяется перестановкой столбцов, которые приходилось делать по ходу вычислений.

Последние (m-r) уравнений следует понимать как

Если хоть одно из , то получим несовместную систему уравнений (т.е. не имеющую решений). Таким образом для всякой совместной системы . Тогда эти выражения можно опустить. Переносим в (3.12) все члены, содержащие в правую часть, тогда

(3.13)

Здесь ( ) – свободные переменные, им можно придавать произвольные значения. Неизвестные определяются однозначно. Из последнего уравнения находим , далее подставляем в предпоследнее, находим и т.д..

Пример 3.2. Решить систему уравнений:

Решение. Расширенная матрица системы

.

Умножаем каждый элемент 1-й строки на(-3) и складываем со 2-й строкой.Умножаем каждый элемент 1-й строки на(-2) и складываем с 3-й строкой. Получаем:

.

Умножаем каждый элемент 2-й строки на( ) и складываем с 3-й строкой. Получаем

.

Тогда r(A) = r(A/B) =3 – система совместна.

Полученной матрице соответствует система

,

откуда z = 1; y=1; x=1.

Пример 3.3. Решить систему уравнений:

Решение. Расширенная матрица системы имеет вид

.

Умножаем каждый элемент 1-й строки на(-3) и на (-4) и складываем со второй и третьей строкой соответственно. Получим:

.

Умножаем каждый элемент 2-й строки на(-1) и сложим с 3-й. Получим :

.

Ранг матрицы системы r(A)=2, ранг расширенной матрицы r(A/B)=3, r(A)≠r(A/B), следовательно система несовместна.

Пример 3.4. Решить систему уравнений:

Решение. Расширенная матрица системы имеет вид

~ ~ ~ ,

r(A)=2; r(A/B)= 2 => система совместна. Тогда

где z – свободная переменная, z = t, тогда x =1, y = -t, z = t.

Однородная система имеет либо единственное тривиальное решение, т.е. x = y = z = 0, если ≠0 и ранг матрицы равен числу неизвестных, причем число неизвестных равно числу уравнений, либо имеет бесчисленное множество решений в противном случае.

Вопросы для самопроверки

1. Что называется матрицей и расширенной матрицей системы линейных уравнений?

2. Что называется решением системы линейных уравнений? Какие системы называются совместными, а какие – несовместными?

3. Сформулируйте теорему Кронекера-Капелли.

4. Напишите формулы Крамера. В каком случае они применимы?

5. При каком условии система линейных уравнений имеет единственное решение?

6. Что можно сказать о системе линейных уравнений, если ее определитель равен нулю?

7. При каком условии система n линейных уравнений с n неизвестными имеет ненулевое решение?

8. Опишите метод Гаусса решения систем линейных уравнений.

9. В чем состоит матричный способ решения систем линейных уравнений?