9. Преобразование систем координат

Выделяются два случая преобразования одной прямоугольной системы координат в другую: параллельный перенос осей координат и поворот осей координат.

Рассмотрим параллельный перенос осей координат, при котором направление осей и масштаб остаются неизменными, а меняется положение начала координат. Начало новой системы координат точка имеет координаты в старой системе координат хОу , т.е. . Координаты произвольной точки М плоскости в системе хОу обозначим через (х,у), а в новой системе - через (рис. 30).

Из рисунка видно, что

(9.1)

Н айденные формулы позволяют находить старые координаты х,у по известным новым кординатам и наоборот. Рассмотрим поворот осей координат как преобразование, при котором начало координат и масштаб не меняются, а обе оси поворачиваются на один и тот же угол . Новая система координат получена поворотом старой системы координат на угол  . Произвольная точка М имеет относительно старых осей координаты , а относительно новых осей - координаты .

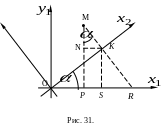
На рис. 31 Из прямоугольного треугольника следует, что

а из прямоугольного треугольника следует, что . Отсюда получаются уравнения связи координат точки в исходной системе координат и повернутой системе координат

(9.2)

10. Приведение общего уравнения кривой второго порядка к каноническому виду

Линией второго порядка в декартовых координатах называется линия, определяемая уравнением второй степени с двумя неизвестными:

. (10.1)

Центром линии второго порядка является точка плоскости, совпадающая с центром симметрии кривой, если таковой имеется. В качестве примера центральной линии второго порядка можно назвать эллипс и гиперболу. Центр у линии второго порядка существует, если найдется единственная точка , координаты которой будут удовлетворять системе уравнений:

(10.2)

Система уравнений имеет единственное решение, если главный определитель , называемый дискриминантом, будет отличен от нуля:

(10.3)

В этом случае по формулам Крамера

Если центр линии определен, то уравнение кривой упрощается при переходе к новым координатам системы координат , полученной из старой системы координат путем параллельного переноса. Используя уравнения связи координат при параллельном переносе

,

получаем уравнение линии в виде

где

Следующий этап упрощения связан с поворотом системы координат на угол , задаваемый формулами (9.2).

Выразим в уравнении линии старые координаты через новые:

Выберем угол  таким образом, чтобы коэффициент при обратился в ноль

При подстановке найденного значения угла в уравнение линии последнее приобретает вид

где

Если то уравнение для тангенса угла поворота теряет смысл. В этом случае из чего следует, что систему координат требуется повернуть на

Пример 10.1. Уравнение привести к каноническому виду путем преобразования систем координат.

Решение. Перейдем к смещенной системе координат, вычислив предварительно координаты центра кривой .

Старые координаты х, у связаны с новыми координатами уравнениями

Уравнение кривой в координатах примет вид

,

Перейдем к системе координат , повернутой относительно предыдущей системы координат на угол , для чего воспользуемся формулами связи координат при повороте (9.2).В результате получим

+

+

Угол поворота выбирается из условия обращения в ноль коэффициента при :

6sin cos -4 +4 =0.

Вычисление дает tg ₁=2, tg ₂= -1/2.

Условимся выбрать в первой четверти, тогда tg =2,

а sin =tg / =2/ , cos =1/ =1/ .

Используя найденные тригонометрические функции, получим уравнение

которое после деления на свободный член приобретет вид уравнения эллипса с полуосями =1/2, =3/4.

Если кривая второго порядка не является центральной, т.е. дискриминант =0, упрощение уравнения рекомендуется начинать с поворота системы координат указанным выше способом, после чего с помощью параллельного переноса системы координат производится дальнейшее упрощение вида уравнения. В качестве примера нецентральной кривой второго порядка можно указать параболу.