7.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых. Расстояние от точки до прямой.
Определение
угла между прямыми сводится к определению
угла между их направляющими векторами
;
.
Из определения скалярного произведения имеем:
(7.5)
- угол между прямыми в пространстве.
Условие
параллельности прямых эквивалентно
условию коллинеарности их направляющих
векторов
и
:
(7.6)
- условие параллельности прямых в пространстве.
Условие перпендикулярности прямых: ( , ) = 0:
l1l2 + m1m2 +n1n2 = 0 (7.7)
- условие перпендикулярности прямых в пространстве.
Пример
7.4 . Найти
угол между прямой
и
прямой, проходящей через две точки
.
Решение.
Координаты направляющего вектора первой
прямой
.
Для второй прямой направляющим является
вектор
.
Угол между направляющими векторами
вычислим, используя формулу (7.5),
.
Расстояние от точки до прямой
Расстояние
от точки
до прямой
вычисляется
по формуле
(7.8)
Пример
7.5. Найти
расстояние от точки
до прямой
Решение.
Воспользуемся
формулой
(7.8). Так как
то
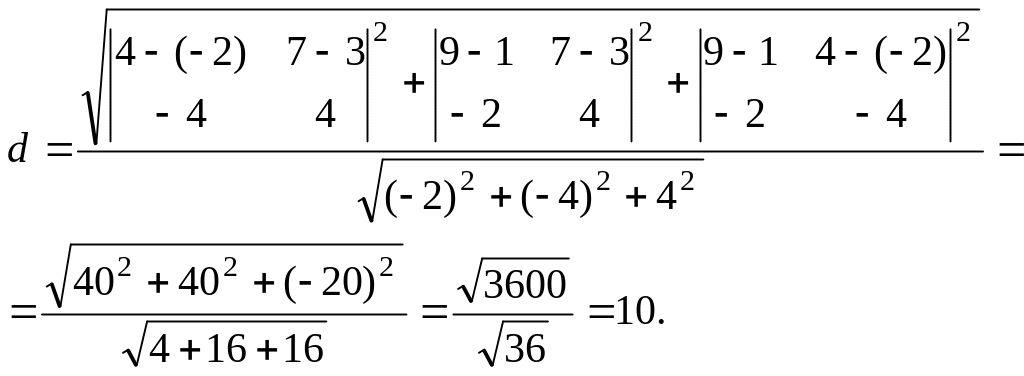
Итак, расстояние равно 10.
7.5. Условие принадлежности двух прямых к одной плоскости
Две прямые в пространстве могут:
1. пересекаться;
2. быть параллельными;
3. скрещиваться.
В первых двух случаях прямые лежат в одной плоскости.
Пусть прямые и заданы каноническими уравнениями:
;
.
Для принадлежности двух прямых к одной плоскости необходимо и достаточно, чтобы три вектора
,
(
и
точки на прямых
и
),
были компланарны, т.е. смешанное
произведение этих векторов равно нулю.
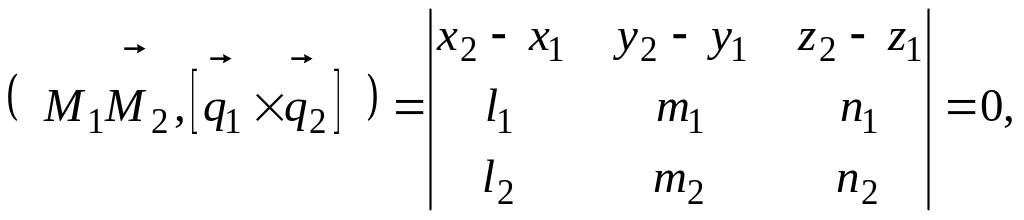(7.8)
- условие принадлежности двух прямых одной плоскости.
Пример 7.5. Доказать, что прямые
пересекаются.
Решение. Применим формулу (7.8).
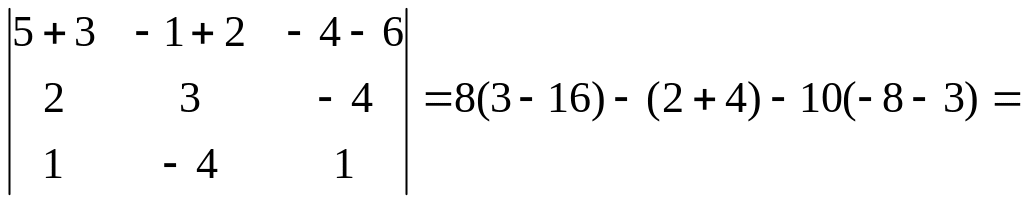
=-104 – 6 + 110 = 0.
Таким образом прямые лежат в одной плоскости. А так как координаты их направляющих векторов не пропорциональны, следовательно прямые не параллельны, а пересекаются. Что и требовалось доказать.
7.6. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
Р
ассмотрим
плоскость p,
заданную уравнением
и прямую
,
заданную каноническими уравнениями:
Поскольку
угол j
между прямой
и плоскость p
является дополнительным к углу между
вектором нормали плоскости
и
направляющим вектором прямой
,
то (
,
)=
; cosy
= cos(900
- j)
= sinj,
то
(7.9)
- угол между прямой и плоскостью.
Условие параллельности прямой и плоскости эквивалентно условию перпендикулярности направляющего вектора прямой и нормального вектора плоскости
Аl +Bm +Cn = 0 (7.10)
- условие параллельности прямой и плоскости.
Условие
перпендикулярности прямой и плоскости
эквивалентно условию параллельности
и
(7.11)
- условие перпендикулярности прямой и плоскости.
Пример
7.6. При каком
значении
и
прямая
и плоскость
перпендикулярны?
Решение.
Воспользуемся условием перпендикулярности
прямой и плоскости (7.11). Тогда
.
Получаем
Пример 7.7. При каком значении n прямая
параллельна
плоскости
.
Решение.
Обращаемся
к условию параллельности прямой и
плоскости (7.10). Подставляя соответствующие
значения в это уравнение, получим
или
откуда
