Теорема. Два ненулевых вектора и составляют острый (тупой) угол тогда и только тогда, когда их скалярное произведение положительно (отрицательно). Алгебраические свойства скалярного произведения

1. (переместительное свойство).

2. (сочетательное свойство относительно числового множителя).

3. (распределительное свойство относительно суммы векторов).

4. , если - ненулевой вектор,

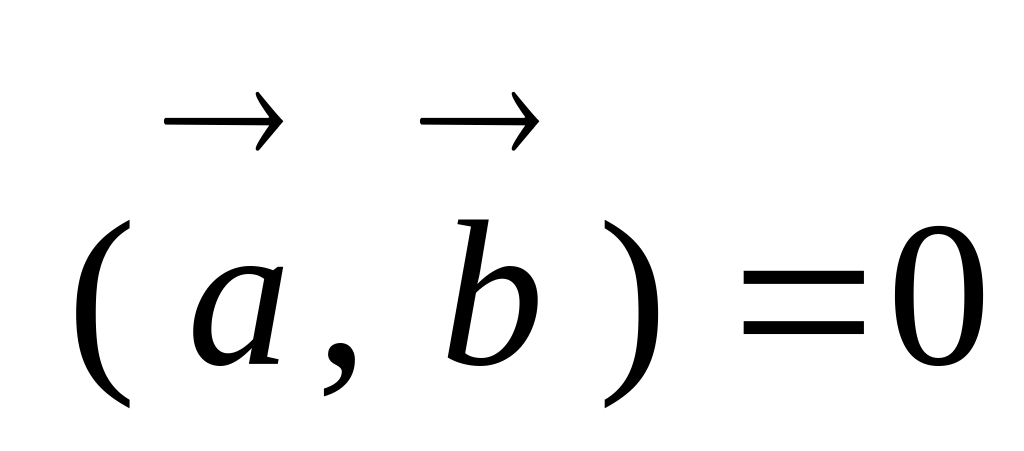5. , если - любой вектор.

Действительное векторное пространство с определенным нами скалярным произведением называется евклидовым пространством.

Скалярное произведение очень просто выражается через координаты векторов и в базисе , а именно:

Теорема. Если два вектора и определены своими декартовыми прямоугольными координатами: ; , то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат, то есть

, (4.13)

Теорема доказывается путем почленного скалярного перемножения многочленов

Отметим, что скалярное произведение для системы единичных базисных векторов обладает свойством:

при , то есть

Следствие 1. Необходимым и достаточным условием ортогональности векторов и является равенство

.

Следствие 2. Угол между векторами определяется формулой

(4.14)

Следствие 3. Модуль вектора

4.7.2. Векторное произведение векторов

Для определения векторного произведения векторов введем определения правых и левых троек векторов и системы координат.

Определение. Три вектора называются упорядоченной тройкой (или просто тройкой), если указано, какой из этих векторов является первым, какой – вторым и какой – третьим. Например, .

Определение. Тройка некомпланарных векторов называется правой (левой), если выполнено одно из условий:

1) если, будучи приведенными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки;

2) если после приведения к общему началу вектор располагается по ту сторону от плоскости, определяемой векторами и , откуда кратчайший поворот от к кажется совершающимся против часовой стрелки (по часовой стрелке);

3) если, находясь внутри телесного угла, образованного приведенными к общему началу векторами , мы видим поворот от к и от него к совершающимся против часовой стрелке (по часовой стрелке).

Эти три условия эквивалентны.

Из трех векторов можно составить шесть троек:

; ; одной ориентации;

; ; противоположной ориентации.

Определение. Декартова система координат называется правой (левой), если три базисных вектора образуют правую (левую) тройку.

В дальнейшем будем рассматривать только правые системы координат.

Определение. Векторным произведением вектора на вектор называется вектор , обозначаемый символом и удовлетворяющий трем требованиям:

1. длина вектора равна произведению длин векторов и на синус угла между ними, то есть

; (4.15)

2. вектор ортогонален к каждому из векторов и ;

3. вектор направлен так, что тройка векторов является правой.

Физический смысл векторного произведения: вектор есть момент силы , приложенной в точке , относительно точки , из которой в точку идет вектор .

Геометрические свойства векторного произведения

Теорема. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Теорема. Длина (или модуль) векторного произведения равняется площади S параллелограмма, построенного на приведенных к общему началу векторах и .

Введем определение орта: ортом произвольного ненулевого вектора назовем единичный вектор, коллинеарный и имеющий одинаковое с направление.

Следствие из теоремы. Если - орт векторного произведения , а S – площадь параллелограмма, построенного на приведенных к общему началу векторах и , то для векторного произведения справедлива формула

, (4.16)

где тройка векторов - правая.