Эйлеров цикл: определение, условие существования, алгоритм нахождения
Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу.
Эйлеров цикл — это эйлеров путь, являющийся циклом, то есть замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.
Условие существования:
В неориентированном графе эйлеров цикл существует тогда и только тогда, когда граф связный или будет являться связным, если удалить из него все изолированные вершины, и в нём отсутствуют вершины нечётной степени.
В ориентированном графе эйлеров цикл существует тогда и только тогда, когда он сильно связан (то есть из любой вершины графа существует ориентированный путь в любую другую) или среди его компонент сильной связности только одна содержит ребра (а все остальные являются изолированными вершинами) и для каждой вершины графа её входящая степень любой вершины равна её выходной степени.
Алгоритм нахождения:
Для поиска эйлерова цикла воспользуемся тем, что эйлеров цикл — это объединение всех простых циклов графа. Следовательно, задача — эффективно найти все циклы и эффективно объединить их в один.
Реализовать это можно, например, так, рекурсивно:
procedure FindEulerPath (V)
1. перебрать все рёбра, выходящие из вершины V; каждое такое ребро удаляем из графа, и вызываем FindEulerPath из второго конца этого ребра;
2. добавляем вершину V в ответ.
Сложность полученного алгоритма — O(M), то есть линейная относительно количества рёбер М в данном графе.
Гамильтонов цикл: определение, алгоритм нахождения на основе динамического программирования
Гамильтонов цикл – цикл проходящий через каждую вершину графа ровно один раз. Граф который имеет гамильтонов цикл называется гамильтонов граф.
Деревья: остовное дерево, алгоритм Крускала
Остовное дерево — ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины.
Понятие остовный лес неоднозначно, под ним могут понимать один из следующих подграфов:
любой ациклический подграф, в который входят все вершины графа, но не обязательно связный;
в несвязном графе — подграф, состоящий из объединения остовных деревьев для каждой его компоненты связности.
Остовное дерево также иногда называют покрывающим деревом, остовом или скелетом графа. Ударение в слове «остовный» у разных авторов указывается на первый (от слова о́стов) или на второй слог.
П
ример
минимального остовного дерева.
Свойства
Любое остовное дерево в графе с n вершинами содержит ровно n-1 ребро.
Число остовных деревьев в полном графе на n вершинах равно n^{n-2}; это утверждение называется формулой Кэли
Число остовных деревьев в полном двудольном графе Km.n равно mn-1*nm-1
В общем случае, число остовных деревьев в произвольном графе может быть вычислено при помощи так называемой матричной теоремы о деревьях.
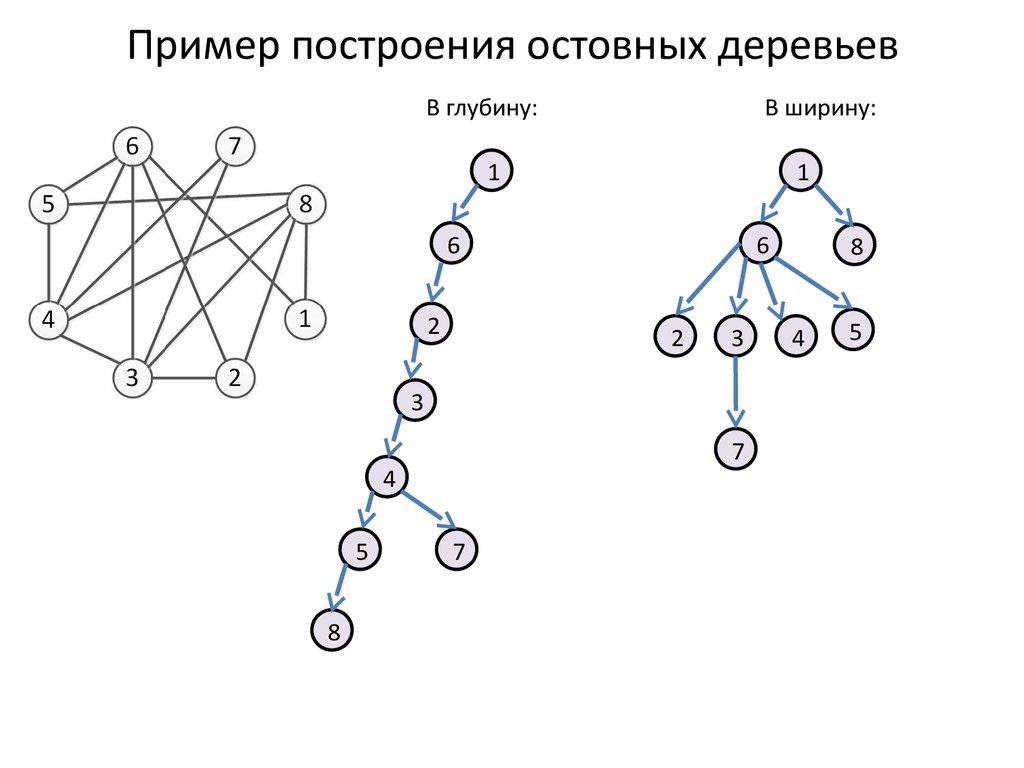
Остовное дерево может быть построено практически любым алгоритмом обхода графа, например поиском в глубину или поиском в ширину. Оно состоит из всех пар рёбер u,v), таких, что алгоритм, просматривая вершину u, обнаруживает в её списке смежности новую, не обнаруженную ранее вершину v.
Остовные деревья, построенные при обходе графа алгоритмом Дейкстры, начиная из вершины s, обладают тем свойством, что кратчайший путь в графе из s до любой другой вершины — это (единственный) путь из s до этой вершины в построенном остовном дереве.
Существует также несколько параллельных и распределённых алгоритмов нахождения остовного дерева. Как практический пример распределённого алгоритма можно привести протокол STP.
Если каждому ребру графа присвоен вес (длина, стоимость и т. п.), то нахождением оптимального остовного дерева, которое минимизирует сумму весов входящих в него рёбер, занимаются многочисленные алгоритмы нахождения минимального остовного дерева.
Задача о нахождении остовного дерева, в котором степень каждой вершины не превышает некоторой наперёд заданной константы k, является NP-полной/
Алгоритм Краскала (англ. Kruskal's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе.
Будем последовательно строить подграф F графа G ("растущий лес"), пытаясь на каждом шаге достроить F до некоторого MST. Начнем с того, что включим в F все вершины графа G. Теперь будем обходить множество E(G) в порядке неубывания весов ребер. Если очередное ребро e соединяет вершины одной компоненты связности F, то добавление его в остов приведет к возникновению цикла в этой компоненте связности. В таком случае, очевидно, e не может быть включено в F. Иначе e соединяет разные компоненты связности F, тогда существует ⟨S,T⟩ разрез такой, что одна из компонент связности составляет одну его часть, а оставшаяся часть графа — вторую. Тогда e — минимальное ребро, пересекающее этот разрез. Значит, из леммы о безопасном ребре следует, что e является безопасным, поэтому добавим это ребро в F. На последнем шаге ребро соединит две оставшиеся компоненты связности, полученный подграф будет минимальным остовным деревом графа G. Для проверки возможности добавления ребра используется система непересекающихся множеств.
