3. Состоятельность оценки; примеры состоятельных и несостоятельных оценок

При обработке выборки исследователь интуитивно предполагает, что, чем больше ее объем, тем ближе будет оценка к истинному значению. Т.е. с ростом N, ошибка в оценивании должна стремиться к нулю. Это возможно, если алгоритм оценки эффективно использует ту информацию об искомом параметре, которая содержится в выборке. 

Формально данное свойство определяется следующим образом: оценка является состоятельной, если сходится по вероятности к , то есть:

Для любого θ: NА p→ при N → ∞

То есть оценку параметра называют состоятельной, если с ростом объёма выборки N она сходится по вероятности к оцениваемому параметру.

Несостоятельная оценка – оценка, которая не сходится по вероятности к оцениваемому параметру с ростом выборки.

Сходимость по вероятности в свою очередь означает, что для любого, сколь угодно малого, отличного от нуля :

То есть всегда найдется такой объем выборки, который с вероятностью, близкой к единице обеспечит необходимую величину ошибки в оценивании , какой бы малой она не была. 

На практике «увидеть» сходимость «почти наверное» не представляется возможным, поскольку выборки конечны. Таким образом, для прикладной статистики достаточно требовать состоятельности оценки. 

Пример состоятельной оценки: 

При анализе трафика, передаваемого с сервера на компьютеры клиентов, производится оценка среднего размера пакета передаваемого по сети. Для этого из общего потока выбирается N пакетов, размеры которых фиксируются и усредняются. В данном примере случайная величина характеризует размер пакета, искомый параметр - среднее значение (т.е. ), элементы выборки - размеры зарегистрированных пакетов, алгоритм оценивания 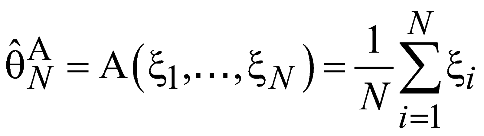. Проверим, является ли данная оценка смещенной:

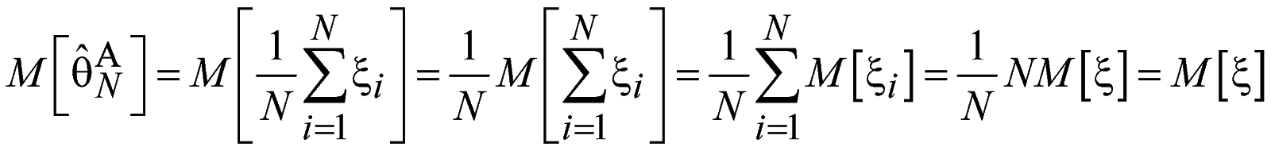
Таким образом, данная оценка является несмещенной, то есть  и можно применить второе неравенство Чебышева.

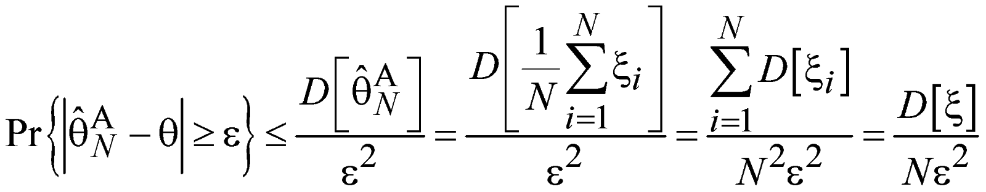
Очевидно, что при конечной для 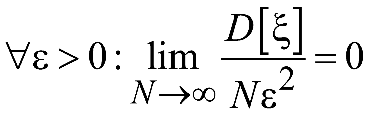, что доказывает состоятельность рассмотренной оценки.

Выборочное среднее  X= 1ni=1nXi  является сильно состоятельной оценкой математического ожидания Xi.

Вообще, все (за редчайшими исключениями) оценки параметров, используемые в вероятностно-статистических методах принятия решений, являются состоятельными.

4. Эффективность оценки; функции штрафа и риска

Предположим, что для проведения эксперимента перед исследователем стоит выбор одного из двух алгоритмов оценивания искомого параметра системы. Оба алгоритма обеспечивают оценки несмещенные и состоятельные. Как осуществить выбор одного из них? Для ответа на этот вопрос вводят третий параметр оценки – параметр эффективности. Прежде, чем дать формальное определение эффективности, дадим ее качественную интерпретацию. На рис. 1 для двух гипотетических оценок приводятся графики зависимости погрешности оценивания от объема выборки. Не смотря на то, что оба алгоритма обеспечивают сколь угодно малую погрешность при , при конечном N алгоритм 2 явно кажется более предпочтительным, т.е. оценка 2 эффективнее оценки 1.

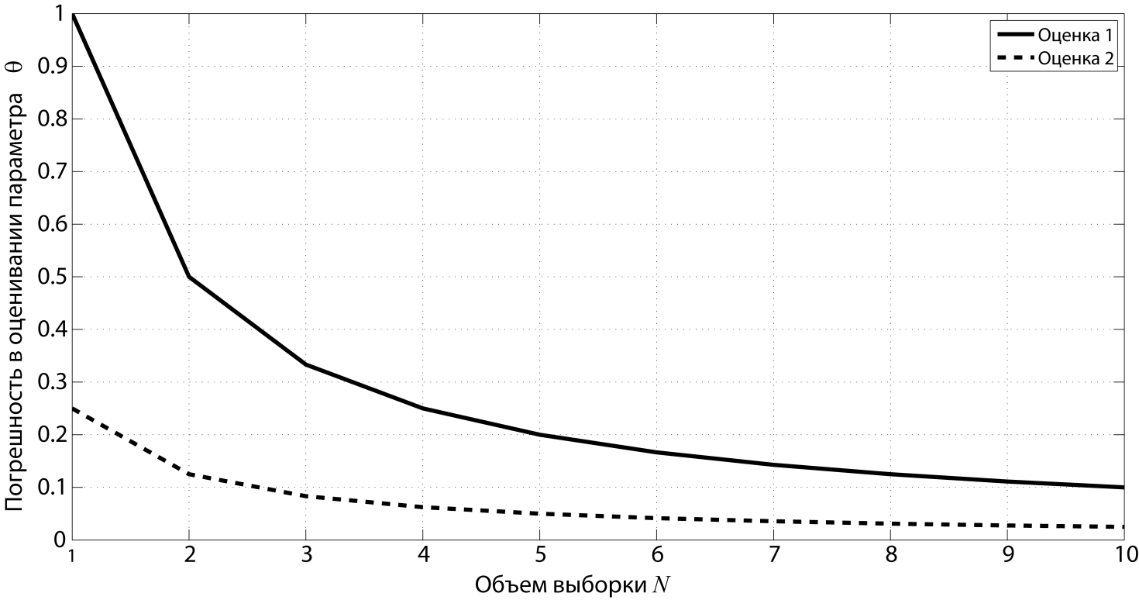
Рис. 1. Сравнение двух алгоритмов оценивания.

Чтобы количественно измерять эффективность введем несколько вспомогательных функций.

Функцией штрафа называется функция, характеризующая меру негативных последствий, возникающих при той или иной ошибке e оценивания параметра системы. Как правило, чем больше , тем больше значение . Функция штрафа выбирается исходя из специфики той предметной области, в которой ведется статистический анализ и может принимать достаточно сложный вид.

Пример иллюстрирующий функцию штрафа

По данным Гидрометцентра проводится оценка количества осадков, выпавших в некотором регионе. Из количества осадков рассчитывается тип и объем удобрений, которые необходимо применить на сельскохозяйственном поле. Известно, что неправильно выбранный режим удабривания приводит к падению количества урожая. Тогда, функция штрафа может иметь, например, вид, приведенный на рис. 2.

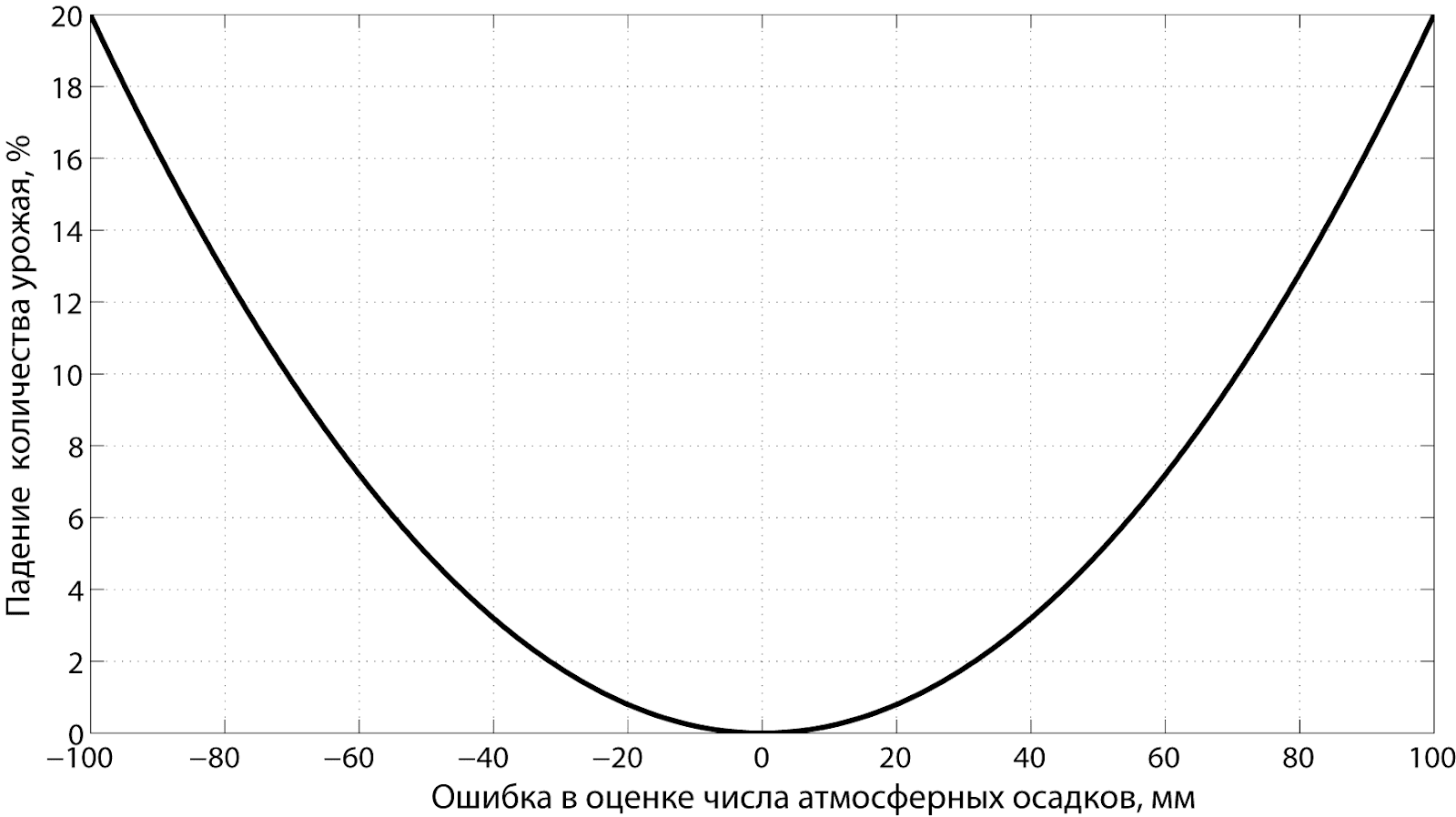
Рис. 2 Функция штрафа в примере, иллюстрирующем функцию штрафа.

Пример иллюстрирующий функцию штрафа 2

В ходе работы телекоммуникационной системы приемник периодически проводит оценку мощности шумов, присутствующих в канале. Этот уровень учитывается в процессе декодирования принимаемого сообщения. Известно, что ошибочно введенная в декодер информация о шумах повышает вероятность битовой ошибки при приеме данных. При этом заниженная оценка мощности приводит к существенно большему ухудшению качества приема, нежели завышенная. Типичная функция штрафа приведена на рис. 3.

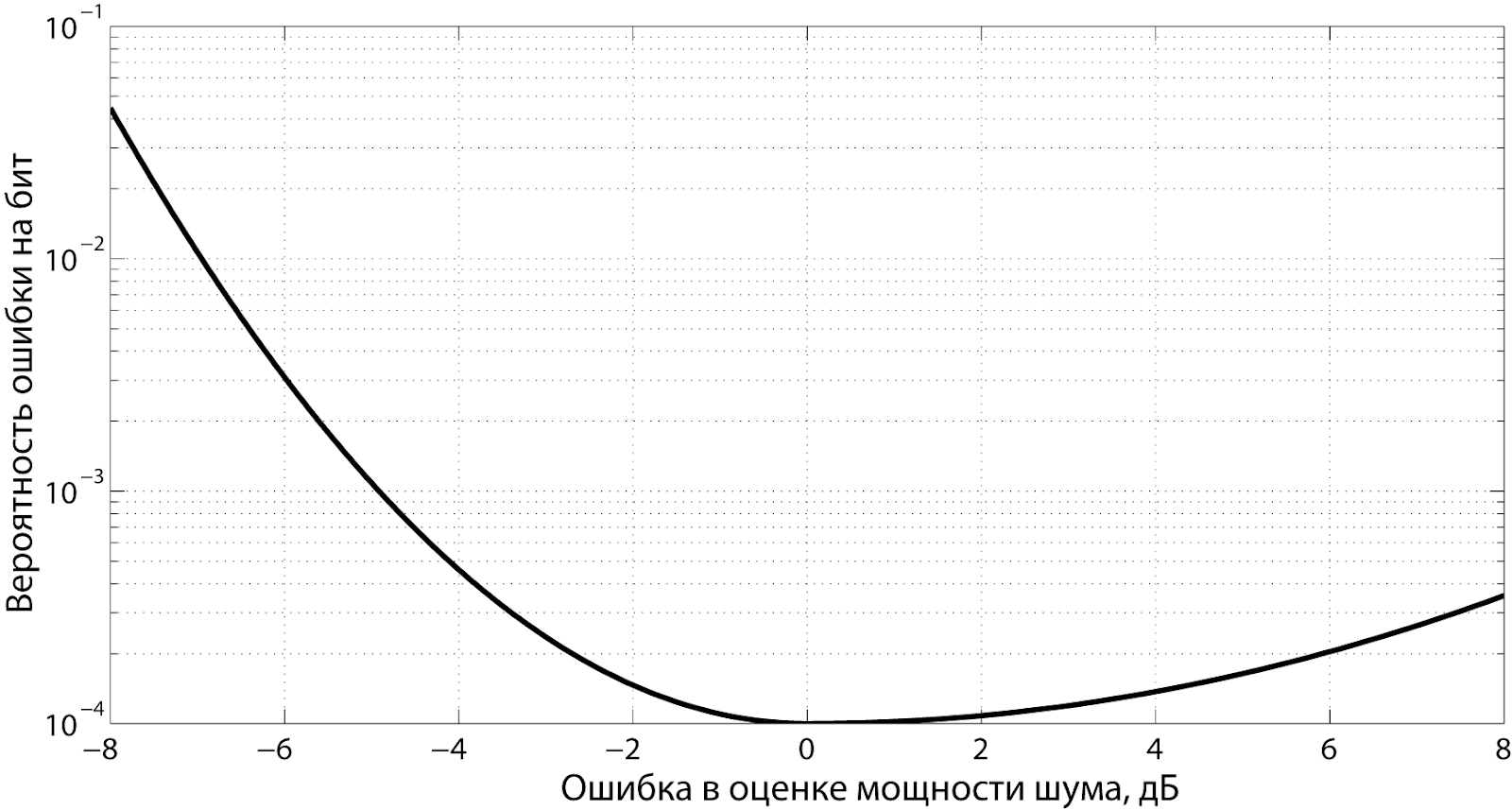
Рис. 3 Функция штрафа в примере, иллюстрирующем функцию штрафа 2.

Как правило, многие реальные функции штрафа могут быть хорошо аппроксимированы так называемой квадратичной штрафной функцией или абсолютной штрафной функцией .

Оценка параметра является случайной величиной, а, значит, ошибка в оценивании и величина штрафа также являются случайными величинами. Таким образом, вводят функцию риска:

.

Т.е. функция риска характеризует средний штраф, который заплатит исследователь при использовании алгоритма для оценки параметра по выборке объема N. Более эффективной является та оценка, которая обеспечивает меньший риск.

Стоит отметить, что для несмещенных оценок в случае применения квадратичной штрафной функции:

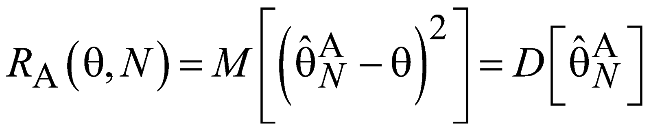
Т.е. функция риска совпадает с дисперсией оценки.

Как можно видеть, функция риска зависит как от объема выборки, так и от истинного значения параметра . Таким образом, для различных диапазонов значения разные оценки могут оказаться более или менее эффективными. При этом ожидается, что для состоятельных оценок (функция риска) убывает с ростом N. Следующий пример иллюстрирует эту зависимость:

Проводится эксперимент, в ходе которого выясняется вероятность потери пакета при передаче по вычислительной сети. Для этого по сети передаются N тестовых пакетов, успешный прием или потеря которых регистрируется на приемной стороне. Вводится величина , равная единице, в случае, если i-й пакет оказался утерянным, и нулю иначе. Тогда воспользуемся следующей несложной оценкой: 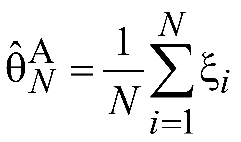. Найдем выражение для случая применения квадратичной штрафной функции. Очевидно, что , тогда:

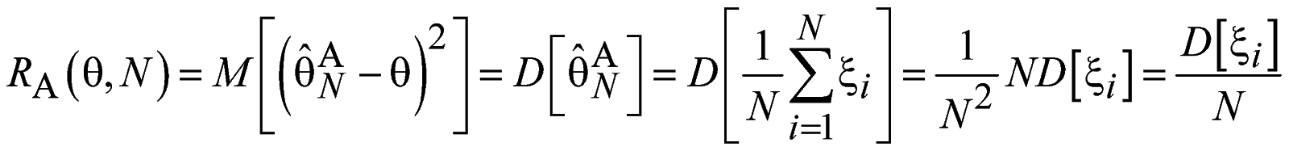
Т.к. является Бернуллиевской случайной величиной с параметром , то:

.
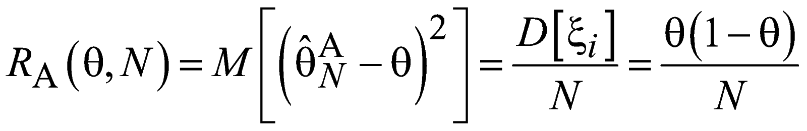