8. Оценка закона распределения случайной величины: метод гистограмм

В основе метода гистограмм лежит идея об аппроксимации плотности вероятности при помощи ступенчатой функции по следующему принципу.

Известно, что вероятность попадания случайной величины в заданный интервал [a, b] находится из следующего выражения:

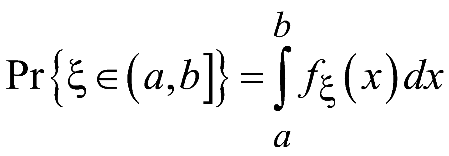
При малой длине (a, b] функцию можно считать на этом интервале почти постоянной и можно воспользоваться следующим приближением:

.

Тогда:

Соответственно можно разбить область определения случайной величины на M непересекающихся интервалов и на каждом интервале аппроксимировать плотность вероятности при помощи выражения (1). Чем больше M и меньше длительности интервалов , тем более точной будет аппроксимация.

По выборке можно осуществить оценку следующим образом:

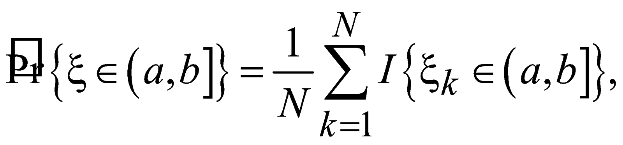
где N – объем выборки, - k-й элемент выборки, - индикатор события t. Тогда оценка плотности вероятности будет иметь следующий вид:

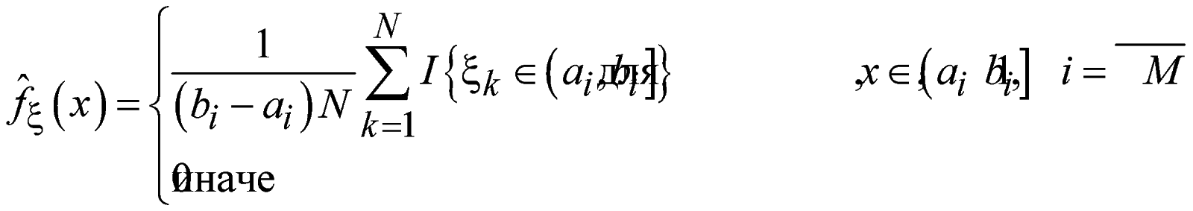
Графическое изображение функции (3) называется гистограммой и имеет характерный ступенчатый вид, будет задана на интервале [a₁, b_M].

Стандартные решения практических вопросов, таких, как оценка области определения случайной величины, выбор числа интервалов M, границы интервалов (a_i, b_i], необходимых для применения выражения (3):

1. Число интервалов разбиения выбирать исходя из правила Стерджеса: 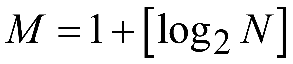, где N – объем выборки, 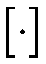– знак округления.

2. Выбор границ области построения гистограммы: , 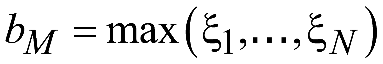. Стоит, иметь в виду, что такой подход может привести к низкой точности оценки плотности вероятности для "тяжелохвостых" распределений. Поэтому, если существует подозрение о тяжелохвостости распределения, можно провести предварительное усечение выборки.

3. Для выбора интервалов (a_i, b_i], как правило, достаточно использовать разбиение интервала 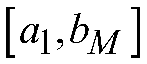на M равных частей длиной 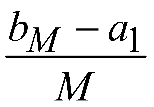. Тогда: , .

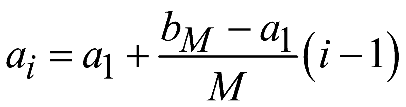Ошибку в оценке плотности вероятности можно количественно охарактеризовать, посчитав средний квадрат относительного отклонения оценки от истинного значения :

                                              

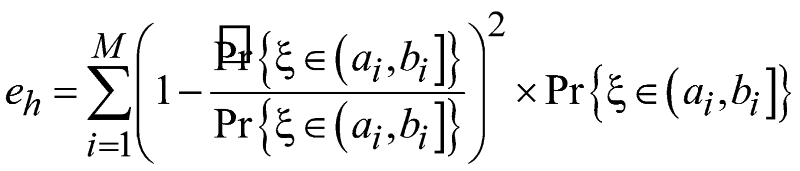
Математическое ожидание величины e_h убывает обратно пропорционально объему выборки N: .

9. Коэффициенты асимметрии и эксцесса; диаграммы Каллена-Фрея

Одним из способов экспресс-оценки распределения является метод диаграмм Каллена-Фрея. Согласно данному методу, по выборке оцениваются коэффициент асимметрии и коэффициент эксцесса, по которым можно приближенно определить класс распределений, к которому принадлежит выборка. 

Коэффициент асимметрии количественно характеризует степень отклонения формы плотности вероятности от симметричной функции:

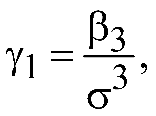
где — третий центральный момент, — среднеквадратическое отклонение. Для симметричных распределений . Знак коэффициента асимметрии указывает на перекос распределения вправо или влево относительно математического ожидания

Коэффициент эксцесса — это мера остроты пика распределения случайной величины:

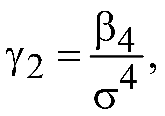
где — четвертый центральный момент. Так, для нормального закона распределения случайной величины: . Законы распределения с более острой вершиной, чем у нормального имеют коэффициент эксцесса более 3 и с менее острой вершиной – менее 3. Поэтому иногда используют нормированный коэффициент эксцесса: . Так, если пик распределения более заостренный, нежели у нормального закона, если же , то менее.

Тогда, по выборке оцениваются , и .      

Из курса теории вероятностей, k-й начальный момент характеризует среднее значение случайной величины, возведенной в степень k. Поэтому алгоритмом оценивания является оценка через выборочный момент:  

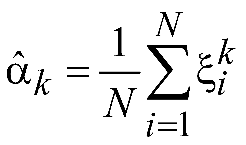
Здесь - оценка k-го центрального момента, N – объем выборки, – значения элементов выборки. 

Зависимость дисперсии оценки от объема выборки в случае независимости ее элементов определяется следующим выражением:

  ,

где - k-й центральный момент. Т.е. дисперсия данной оценки убывает пропорционально объему выборки. Соответственно среднеквадратическое отклонение убывает пропорционально корню из числа элементов в выборке:

     

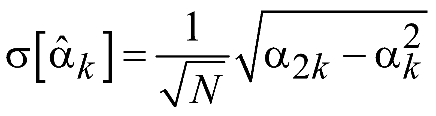
Таким образом, чем больше объем выборки, тем меньше разброс оценки относительно истинного значения момента.

По аналогии с выборочным начальным моментом можно сформулировать понятие выборочного центрального момента.

         

Здесь - истинное значение математического ожидания. На практике, как правило, прямое использование выражения (6) – невозможно, т.к. точное значение – не известно. Однако величина может быть оценена заранее, например, при помощи выражения (1). Выражение (6) при этом принимает вид:

        ,

                      

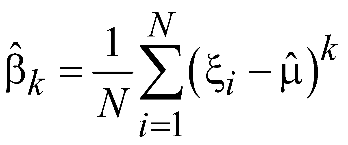которые после подстановки в выражения (1) и (2) дают оценки для искомых коэффициентов. Отложив и на осях диаграммы Каллена-Фрея можно приближенно оценить, к какому классу распределений принадлежит наблюдаемая выборка. Пример диаграммы Каллена-Фрея приведен на рисунке 1.

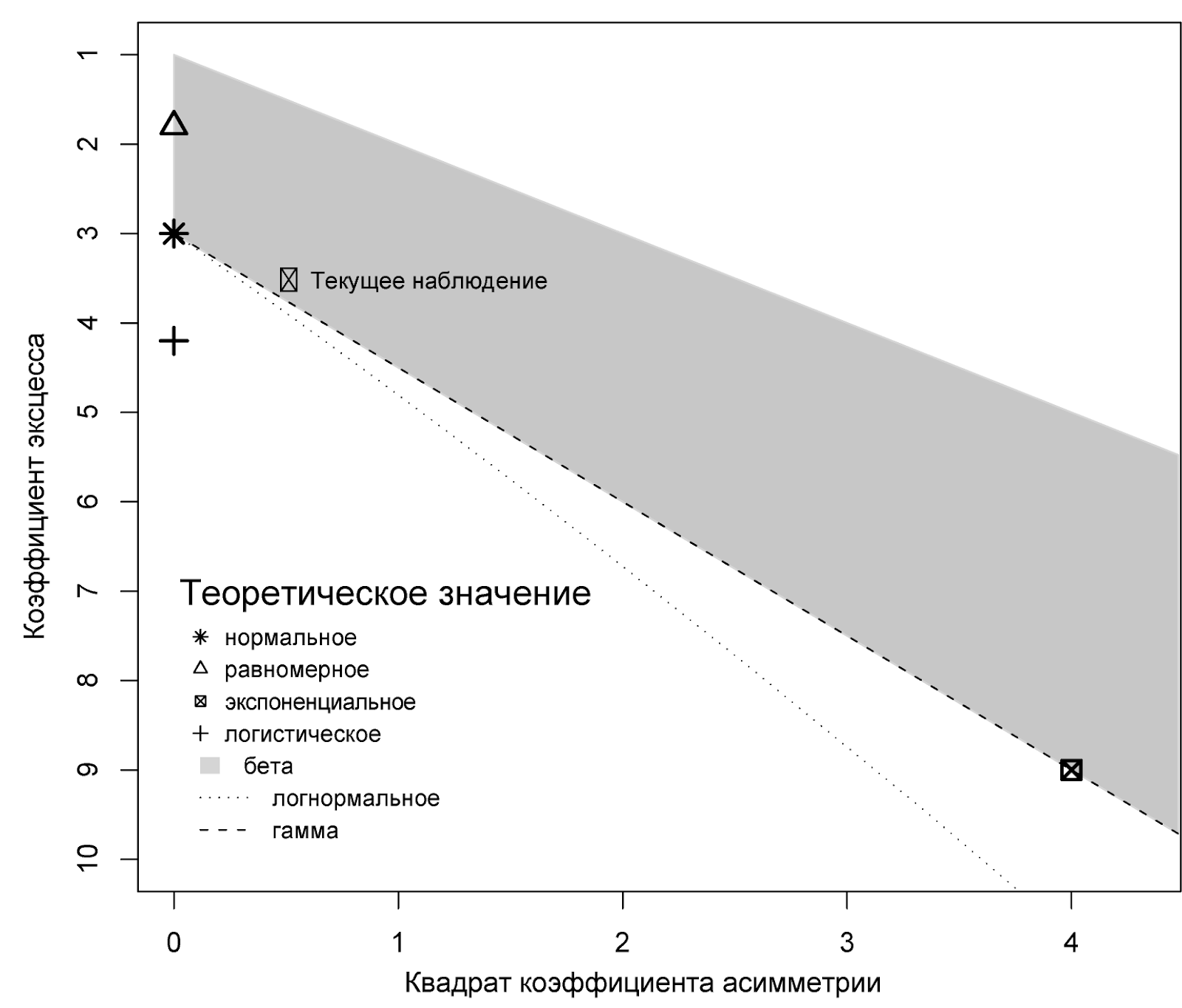
Рисунок 1 – Диаграмма Каллена-Фрея