Метод моментов: пример нахождения параметров равномерного распределения
В тех
случаях, когда исследователю необходимо
провести оценку произвольных
параметров случайной величины (например,
границ в равномерном распределении
или показателя в экспоненциальном)
можно воспользоваться достаточно
универсальным методом
моментов (ММ). Суть
метода заключается в следующем. Параметры
случайной величины однозначно задают
функцию распределения
,
а, значит, и все моменты распределения.
Тогда, если необходимо оценить t
параметров
,
можно составить следующую систему из
t
уравнений:
(1)
Переразрешив
данную систему относительно
,
получим новую систему уравнений,
позволяющую найти параметры распределения
через его моменты:
(2)
После оценки моментов и подстановки их в систему (1) получим оценки для искомых параметров распределения.
Пример нахождения параметров равномерного распределения
По выборке равномерно распределенных случайных величин необходимо одновременно оценить оба параметра данного распределения (левую границу a и правую границу b). Известно, что:
Решив данную систему относительно a и b получим:
Оценив
по выборке
и
и, подставив их в данную систему, получим
оценки по ММ для a
и b.
Очевидным недостатком данного метода является сложность переразрешения системы (1) в систему (2) для некоторых распределений, а также невысокая точность в случае одновременного оценивания большого количества параметров.
Оценка закона распределения случайной величины: эмпирическая интегральная функция распределения
Для
оценки интегральной функции обычно
исходят из определения, согласно
которому
показывает, с какой вероятностью
случайная величина попадает в область
(см. формулу 1.1). Соответственно оценка
может быть осуществлена, например,
следующим способом:
(1)
Оценка
называется эмпирической
интегральной функцией распределения.
Как можно видеть из выражения (1),
является ступенчатой функцией,
скачкообразно изменяющейся в точках
на величину, равную 1/N.
Рисунок 1 – График интегральной и эмпирической интегральной функции для распределения хи-квадрат (объемы выборок – 10, 30, 100)
Очевидно, что чем больше объем выборки N, тем меньше величина «ступеньки» и, значит, тем более точной будет оценка функции . Этот факт выражается в следующих теоремах.
Теорема Гливенко-Кантелли.
Пусть
- бесконечная последовательность из
чисел, распределенных согласно функции
.
Пусть
- эмпирическая интегральная функция
распределения, построенная по первым
N
элементам выборки. Тогда:
.
Здесь
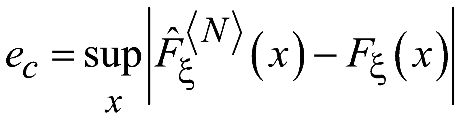обозначает точную
верхнюю грань для
ошибки в оценке. Таким образом,
эмпирическая интегральная функция
распределения является состоятельной
оценкой интегральной функции
распределения.
Теорема Колмогорова.
Скорость сходимости функции к определяется из следующего выражения:
при
Здесь
- случайная величина, распределенная
по закону Колмогорова:
Т. е.
максимальная погрешность в оценке в
среднем убывает обратно пропорционально
корню из объема выборки:
(ср. с выражениями (2.3) и (2.5)).