1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 7. Уравнения математической физики

На заметку

Получить аналитическое решение можно методом разделения переменных. Суть этого метода состоит в следующем. Ищем частное решение исходного уравнения, удовлетворяющее граничным условиям, в виде произведения трех функций, каждая из которых зависит от одной переменной: u(ξ, η, τ) = X(ξ)Y(η)T(τ) . Тогда уравнение может быть записано, после несложных преобразований,

сят от разных независимых переменных, а также принимая во внимание гра-

ральные числа. Мы получили три дифференциальных уравнения. В этих уравнениях важно то, что это обыкновенные дифференциальные уравнения. Их можно решить (найти общее решение). Каждая из функций ищется с точностью до общего несущественного множителя. Принимая этот множитель равным единице, получаем X(ξ) = sin(πmξ) и Y(η) = sin(πnη). Что касается функции , то здесь также нужно учесть нулевое начальное значение для производной по

времени. В этом случае можно показать, что T(τ) = cos(πτ m2 + n2k2 ). Таким образом, общее решение может быть записано в виде линейной комбинации функций вида cos(πτ m2 + n2k2 )sin(πmξ )sin(πnη). Искомым ре-

шением задачи является функция

∞ ∞

u(ξ, η, τ) = ∑∑Amn cos(πτ m2 + n2k2 )sin(πmξ )sin(πnη) , где ко-

m=1 n=1

Следовательно, коэффициенты Anm отличны от нуля только для нечетных ин-

дексов. Сделав формальную замену m → 2m +1 и n → 2n +1, вычисляем

64 1

выражение π6 (2m +1)3(2n +1)3 для отличных от нуля коэффициентов. Не-

посредственно отсюда получаем конечное выражение для аналитического решения задачи.

301

Самоучитель Matlab

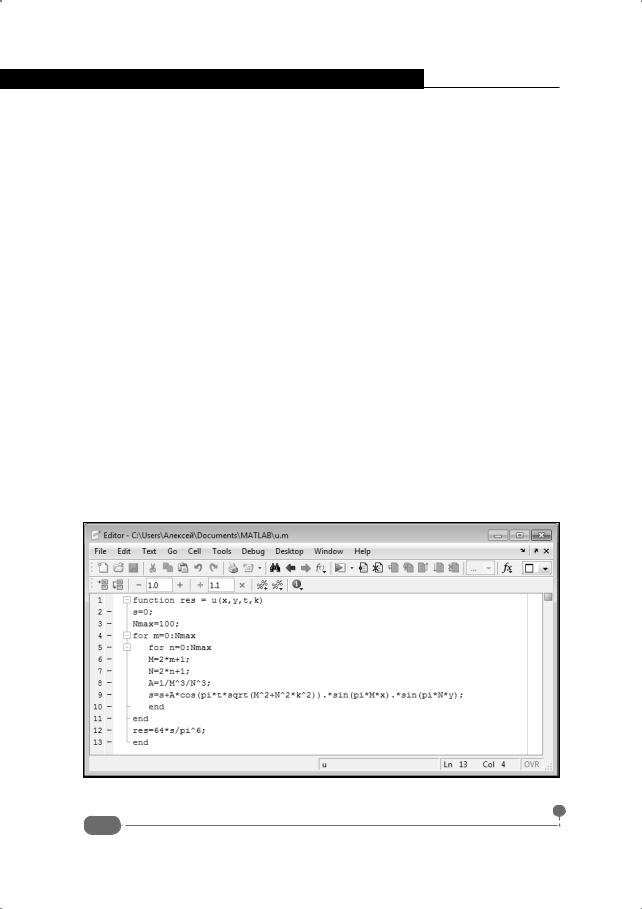
Аналитическое решение используем при составлении программного кода в Matlab. Рассмотрим программный код, представленный ниже, в котором определяется функция – решение задачи:

function res = u(x,y,t,k) s=0;

Nmax=100; for m=0:Nmax

for n=0:Nmax M=2*m+1; N=2*n+1; A=1/M^3/N^3;

s=s+A*cos(pi*t*sqrt(M^2+N^2*k^2)).*sin(pi*M*x).*sin(pi*N*y); end

end res=64*s/pi^6; end

У функции u(), описанной в этом коде, четыре аргумента – кроме двух пространственных переменных (x и y) и времени t, четвертым аргументом указан геометрический фактор k (введенная выше переменная k = L1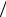L2 ). Все вычисления выполняются в соответствии с приведенными выше формулами. Остановиться можно, пожалуй, лишь на локальных переменных, которые вводятся для упрощения вычислений. Это переменные N и M, а также переменная A. Еще раз подчеркнем, что переменные эти введены исключительно ради удобства. Окно редактора m-файлов с кодом функции представлено на рис. 7.30.

Рис. 7.30. Код функции – решения уравнения в частных производных

302

Глава 7. Уравнения математической физики

Созданную таким образом функцию можно использовать в вычислениях. Например, можно отобразить на графике начальный профиль мембраны. Для этого используем следующие команды:

>>x=0:0.01:1;

>>y=0:0.01:1;

>>[X,Y]=meshgrid(x,y);

>>Z=u(X,Y,0,1);

>>surf(X,Y,Z)

В результате создается поверхность, дающая представление о профиле мембраны в начальный момент времени (рис. 7.31).

Рис. 7.31. Начальный профиль мембраны

Но чтобы представить, что же происходит с течением времени, лучше создать анимацию. В этом случае полезным будет следующий программный код:

%Количество кадров (+1): N=100;

%Продолжительность по времени: T=2;

%Пространственные координаты: x=0:0.01:1;

303

Самоучитель Matlab

y=0:0.01:1;

%Геометрический фактор: k=1;

%Матрицы для графических утилит: [X,Y]=meshgrid(x,y);

for i=0:N

%Момент времени:

t=i*T/N;

%Расчет профиля мембраны: Z=u(X,Y,t,k);

%Поверхность:

surf(X,Y,Z);

%Диапазон значений по осям: axis([0 1,0 1,-1/16 1/16]);

%Координатная сетка:

grid on;

%Кадр анимации: F(i+1)=getframe; end

%Отображение анимации: movie(F,1);

На заметку

Вместо команды movie(F,1) можно воспользоваться инструкцией movie(F).

Сохраняем этот программный код в файле с именем Membrane.m и выполняем с помощью одноименной команды Membrane в командном окне. В результате получаем анимационную картинку, некоторые кадры из которой представлены в табл. 7.1.

На заметку

Для ускорения вычислений можно уменьшить в программном коде для функциирешения дифференциального уравнения количество слагаемых в ряде.

Предложенный выше код (имеется в виду код для функции-решения u()) предназначен для решения конкретной задачи. Его можно сделать более универсальным. В частности, создадим функцию, которая позволит вычислять колебания прямоугольной мембраны с закрепленными краями для произвольного начального профиля мембраны (но при условии, что начальные скорости точек мембраны равны нулю). Другими словами, модифицируем программный код так, чтобы можно было вычислять профиль мембраны в произвольный момент времени, если начальный профиль мембраны задается некоторой функцией f (ξ, η). Рассмотрим приведенный ниже код:

304

Глава 7. Уравнения математической физики

Табл. 7.1. Колебания прямоугольной мембраны

305

Самоучитель Matlab

function s = u2(A,x,y,t,k) s=0;

Nmax=length(A); for m=1:Nmax

for n=1:Nmax s=s+A(m,n)*cos(pi*t*sqrt(m^2+n^2*k^2)).*sin(pi*m*x).*sin(pi*n*y); end

end end

Функцией u2() вычисляется ряд для решения дифференциального уравнения. Особенность функции, по сравнению с предыдущим случаем, состоит в том, что, помимо пространственных переменных x и y, времени t и параметра k, первым аргументом функции передается список A коэффициентов разложения функции начального профиля по базисным функциям. Количество слагаемых в ряде определяется количеством элементов (коэффициентов) в списке A. Коэффициенты этого списка вычисляются с помощью другой функции, которая называется Coefs(). Ее код приведен ниже:

function A=Coefs(f) Nmax=30; A=zeros(Nmax,Nmax); for m=1:Nmax

for n=1:Nmax F=@(x,y)(f(x,y).*sin(pi*m*x).*sin(pi*n*y)); A(m,n)=4*quad2d(F,0,1,0,1);

end

end end

Аргумент у функции один – указатель f на функцию, определяющую профиль начального распределения мембраны. Предполагается, что это функция двух переменных. В теле функции Coefs() определяется переменная Nmax. Ее значение в данном случае равно 100, и это количество слагаемых ряда (по каждой из индексных переменных). Командой A=zeros(Nmax,Nmax) определяется нулевая квадратная матрица, в которую будут заноситься вычисленные коэффициенты разложения. В теле вложенных операторов цикла на основе указателя f командой F=@(x,y)(f(x,y).*sin(pi*m*x).*sin(pi*n*y))

определяется подынтегральная функция, на основе которой вычисляются коэффициенты ряда. Коэффициенты вычисляются командой A(m,n)=4*quad2d(F,0,1,0,1). В этой команде использована функция quad2d(), предназначенная для вычисления интегралов по плоской области. Первым аргументом функции передается указатель на подын-

306

Глава 7. Уравнения математической физики

тегральную функцию. Другие аргументы – пределы интегрирования по каждой из переменных интегрирования.

Для решения задачи создаем файл Membrane2.m со следующим кодом:

%Функция начального профиля: f=@(x,y)exp(-200*((x-0.5).^2+(y-0.5).^2));

%Вычисление коэффициентов:

A=Coefs(f);

%Количество кадров (+1): N=300;

%Продолжительность по времени: T=3;

%Пространственные координаты: x=0:0.02:1;

y=0:0.02:1;

%Геометрический фактор:

k=1;

%Матрицы для графических утилит: [X,Y]=meshgrid(x,y);

for i=0:N

%Момент времени:

t=i*T/N;

%Расчет профиля мембраны: Z=u2(A,X,Y,t,k);

%Поверхность:

surf(X,Y,Z);

%Диапазон значений по осям: axis([0 1,0 1,-0.4 0.4]);

%Координатная сетка:

grid on;

%Кадр анимации: F(i+1)=getframe; end

%Отображение анимации: movie(F);

Функцию начального профиля создаем командой f=@(x,y)exp(-200* ((x-0.5).^2+(y-0.5).^2)). Здесь речь идет о функциональной зависимости f (x,y) = exp(−200(x2 + y2)). Это локализованный в центре квадратной мембраны пик Гауссового типа. В начальный момент мембрана (ее профиль) имеет вид, как на рис. 7.32.

На заметку

Желающие могут подумать, как с минимальными затратами времени и ресурсов построить такой график.

307

Самоучитель Matlab

Рис. 7.32. Начальный профиль мембраны с пиком в центре

Некоторые кадры анимации, созданной в результате выполнения приведенного выше кода, показаны в табл. 7.2.

Табл. 7.2. Колебания мембраны в случае начального профиля в виде пика

308

Глава 7. Уравнения математической физики

309

Самоучитель Matlab

Вообще, картинки получаются достаточно эффектные. К сожалению, не всегда можно с уверенностью сказать, соответствуют ли полученные профили реальному физическому процессу, или это последствие того, что при вычислении ряда было оставлено слишком мало слагаемых. Что поделаешь – ряды по тригонометрическим функциям довольно часто имеют слабую сходимость.

На заметку

Выше был использован подход, при котором коэффициенты разложения ряда вычислялись вне тела функции-решения уравнения. Это было сделано не случайно. Дело в том, что если ряд вычисляется по большому количеству слагаемых, значительное время уходит на расчет этих слагаемых. Если коэффициенты вычислять в теле функции, то такие расчеты будут выполняться каждый раз, когда вызывается функция решения. В использованном выше подходе коэффициенты были вычислены единожды и записаны в матрицу. А при вызове функции решения коэффициенты считываются из этой матрицы. С другой стороны, если матрица очень большая, могут возникнуть проблемы с системными ресурсами, в то время как расчет коэффициентов непосредственно при вызове функции решения можно реализовать так, что использование системных ресурсов сведено к минимуму (зато это будет долго по времени). Тот или иной подход обычно выбирают, исходя из конкретики решаемой задачи и наличия ресурсов для ее решения. В любом случае хорошо, что есть из чего выбирать.

310