1-2 Моделирование / Matlab. Практический подход. Самоучитель

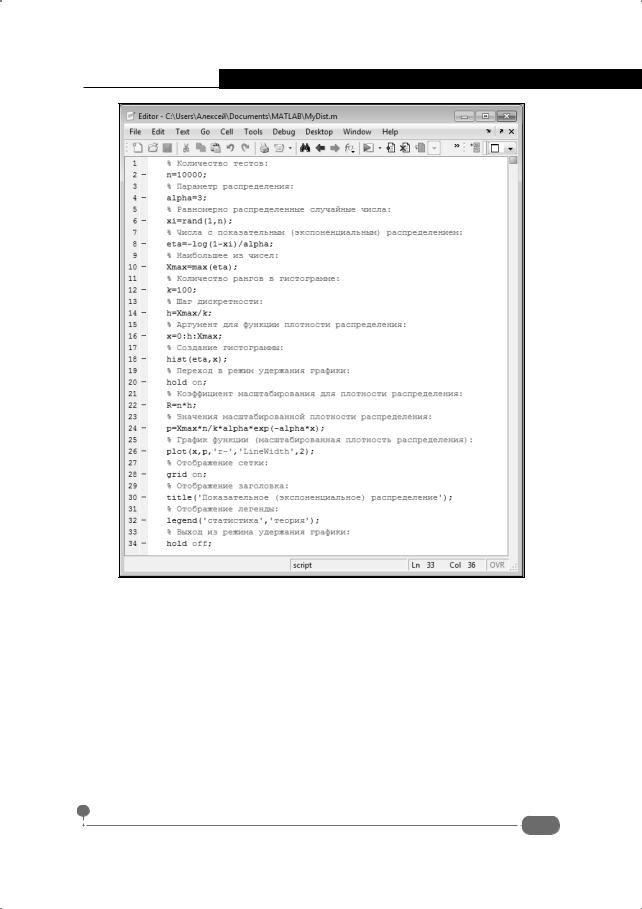
Глава 8. Обработка данных

Рис. 8.24. Генерирование случайных чисел с показательным распределением

Использованный в вычислениях командный код приведен ниже (для удобства восприятия код снабжен комментариями):

%Количество тестов: n=10000;

%Параметр распределения: alpha=3;

%Равномерно распределенные случайные числа: xi=rand(1,n);

%Числа с показательным (экспоненциальным) распределением: eta=-log(1-xi)/alpha;

%Наибольшее из чисел:

Xmax=max(eta);

341

Самоучитель Matlab

%Количество рангов в гистограмме: k=100;

%Шаг дискретности:

h=Xmax/k;

% Аргумент для функции плотности распределения: x=0:h:Xmax;

%Создание гистограммы: hist(eta,x);

%Переход в режим удержания графики: hold on;

%Коэффициент масштабирования для плотности распределения: R=n*h;

%Значения масштабированной плотности распределения: p=Xmax*n/k*alpha*exp(-alpha*x);

%График функции (масштабированная плотность распределения): plot(x,p,'r-','LineWidth',2);

%Отображение сетки:

grid on;

% Отображение заголовка:

title('Показательное (экспоненциальное) распределение');

%Отображение легенды: legend('статистика','теория');

%Выход из режима удержания графики: hold off;

Переменная n определяет количество генерируемых случайных чисел. В принципе, чем это число больше, тем статистическое распределение ближе к теоретической кривой. Параметр распределения α записывается в переменную alpha командой alpha=3 (то есть в нашем случае рассматривается распределение с параметром α = 3 ). Командой xi=rand(1,n) создаем список из равномерно распределенных на интервале от 0 до 1 чисел. Числа с показательным (экспоненциальным) распределением создаем с помощью команды eta=-log(1-xi)/alpha.

Собственно, на этом процесс генерирования случайных чисел с нужным нам распределением завершен. Дальше мы пытаемся проверить, насколько сгенерированные числа (имеются в виду числа в переменной eta – именно эти числа мы будем использовать в дальнейшем) подчиняются экспоненциальному распределению. Делать это будем с помощью графиков. В частности, по набору случайных чисел построим гистограмму распределения случайных чисел по значениям и теоретическую кривую на основе функции плотности экспоненциального распределения.

Для построения графика функции плотности распределения нам понадобится наибольшее из вычисленных чисел (для верхней границы по

342

Глава 8. Обработка данных

аргументу при отображении функции). Наибольшее из случайных чисел вычисляем командой Xmax=max(eta). Переменная k определяет количество рангов в гистограмме (столбцов в диаграмме на один больше). Шаг дискретности по аргументу определяется в соответствии с количеством рангов гистограммы командой h=Xmax/k. Список аргументов для функции плотности распределения вычисляется как x=0:h:Xmax. Эти же значения будем использовать для определения рангов гистограммы. Командой hist(eta,x) создаем гистограмму. Здесь мы использовали встроенную функцию hist() для создания гистограмм. Первым аргументом передается список значений, для которых строится гистограмма, а второй аргумент определяет ранговые значения, для формирования столбцов гистограммы.

На заметку

Если строится гистограмма на основе значений {ηi } (первый аргумент функции hist()), i = 1,2,...,n с ранговой разбивкой в соответствии со списком

{xj } (второй аргумент функции hist()), j = 1,2,...,m , то в результате строится диаграмма, высота столбиков которой равняется количеству значений из списка {ηi }, которые попадают в диапазон между соседними точками xj и xj +1 (для всех возможных индексов). Функция hist() в качестве результата возвращает список со значениями высоты столбцов гистограммы.

Гистограмма дает нам представление о законе распределения случайных чисел. Нам этот закон необходимо сравнить с теоретической кривой для экспоненциального распределения. Соответствующая теоретическая зависимость строится на основе функции плотности распределения. Так, если случайные числа имеют плотность распределения p(x), а всего чисел n , то оценкой (точнее, математическим ожиданием) для количества чисел, попадающих в интервал значений от x до x +dx (при малых значениях dx ), будет значение np(x)dx . В нашем случае роль dx играет переменная h.

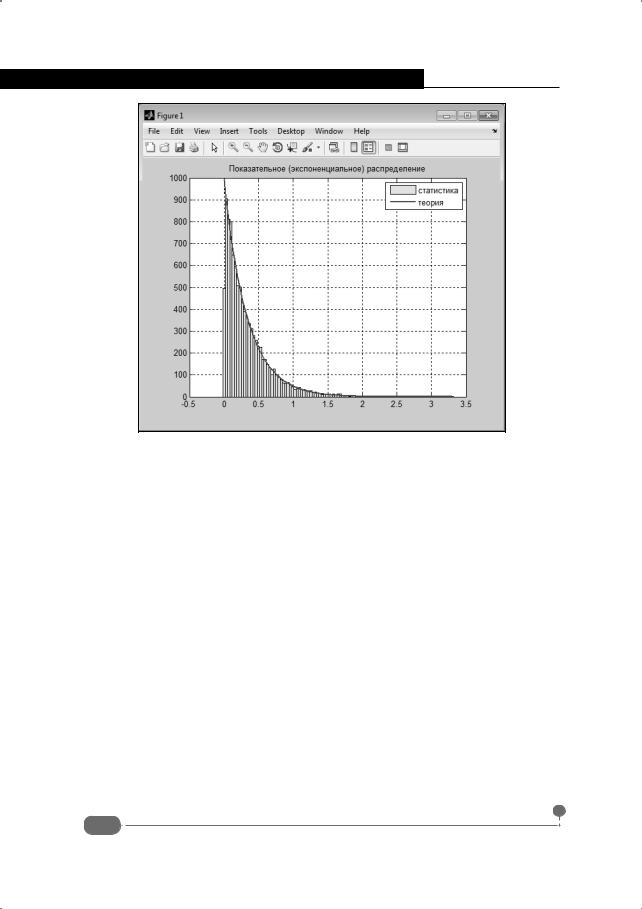
ния R=n*h. Значения "масштабированной" плотности распределения вычисляем командой p=Xmax*n/k*alpha*exp(-alpha*x). Для сравнения командой plot(x,p,'r-','LineWidth',2) строим график теоретической зависимости. Приведенный код сохраняем в файле с именем MyDist.m и в командном окне выполняем команду MyDist. Результаты графических построений представлены на рис. 8.25.

Видим, что совпадение достаточно неплохое. Если увеличить количество генерируемых точек, совпадение будет еще лучше.

343

Самоучитель Matlab

Рис. 8.25. Распределение случайных чисел

Статистические вычисления

- Хотите доказательств?

- Нет, не хочу. Сейчас начнете нудеть, пальцы загибать: "Это раз, это два, это три...". А у меня времени нет. Мне нужно быстренько жирную точку на этом деле поставить.

К/ф "Статский советник"

Существует ряд задач, при решении которых (с разной степенью успешности) могут применяться статистические методы. В качестве примера рассмотрим следующую задачу. Есть набор статистических данных (случайные числа). Известно, что они распределены по нормальному закону с некоторым средним значением a и дисперсией σ2 . Эти параметры неизвестны, и их нужно определить (на основе статистических данных).

Для решения задачи используем метод моментов. Суть его состоит в том, что для определения параметров распределения на основе статистических данных вычисляются эмпирические моменты и приравниваются к соответствующим теоретическим моментам. Теоретические моменты содержат неизвестные параметры распределения. Таким образом, получаем систему алгебраических уравнений, решая которую находим неизвестные параметры распределения.

344

Глава 8. Обработка данных

На заметку

Моментом порядка k случайной величины ξ называется математическое ожидание от величины ξk (обозначается как Mξk ). Момент первого порядка называется математическим ожиданием случайной величины. Если случайная величина имеет плотность распределения p(x), то момент порядка k для этой

лить два параметра, то нас будут интересовать первые два момента, то есть

ские оценки необходимо сравнить с эмпирическими (вычисляемыми по статистическим данным).

На заметку

Эмпирическим моментом порядка k , вычисляемым на основе выборки {xi } n

объема n (то есть i = 1,2,...,n ), называется число mk = 1 ∑xik .

n i=1

Учитывая все приведенные выше обстоятельства, приходим к выводу, что

Документ с исполнительным кодом приведен на рис. 8.26.

Помимо непосредственно вычислений, этот код содержит также и команды для генерирования случайных чисел с параметрами (3, 4) (то есть a = 3 и σ2 = 4 ). Рассмотрим этот код:

n=100000;

x=3+2*randn(1,n);

m1=sum(x)/n;

a=m1;

m2=sum(x.^2)/n; sigma=sqrt(m2-a^2); disp('Параметры распределения:');

disp(['a=',num2str(a),' и sigma=',num2str(sigma)]);

345

Самоучитель Matlab

Рис. 8.26. Определение параметров распределения

Командой n=100000 задается значение для переменной, которая определяет объем генерируемой выборки (количество генерируемых чисел). Числа генерируются командой x=3+2*randn(1,n).

На заметку

Функция randn() генерирует случайные числа со стандартным нормальным распределением, то есть со средним значением a = 0 и дисперсией σ2 = 1 . Нам нужны случайные числа с нормальным распределением и такими параметрами: a = 3 и σ2 = 4 . Легко показать, что если случайная величина ξ имеет стандартное нормальное распределение, то случайная величина η = a + σξ

будет иметь нормальное распределение с параметрами (a, σ2). Поэтому для генерирования чисел с нормальным распределением с параметрами (3, 4) используем инструкцию 3+2*randn(). Это для генерирования одного числа. Для генерирования серии чисел функции randn() передаются аргументы – размеры создаваемого массива из случайных чисел.

Командой m1=sum(x)/n вычисляем эмпирический момент первого порядка (среднее арифметическое). Командой m2=sum(x.^2)/n вычисляется второй эмпирический момент. Стандартное отклонение (корень квадратный из дисперсии σ2 ) вычисляется командой sigma=sqrt(m2-a^2). Перед этим командой a=m1 вычисляется оценка для параметра распределения a. Результаты вычислений выводятся на экран.

На заметку

Здесь мы намеренно не использовали встроенные функции для вычисления статистических характеристик, наподобие mean() (вычисление среднего значения), var() (вычисление дисперсии) или std() (вычисление среднего значения). При использовании встроенных функций необходимо обращать внимание, смещенная или несмещенная характеристики вычисляются. Это замечание актуально для функций var() и std(). Детальное обсуждение особенностей работы этих функций выходит за рамки книги.

346

Глава 8. Обработка данных

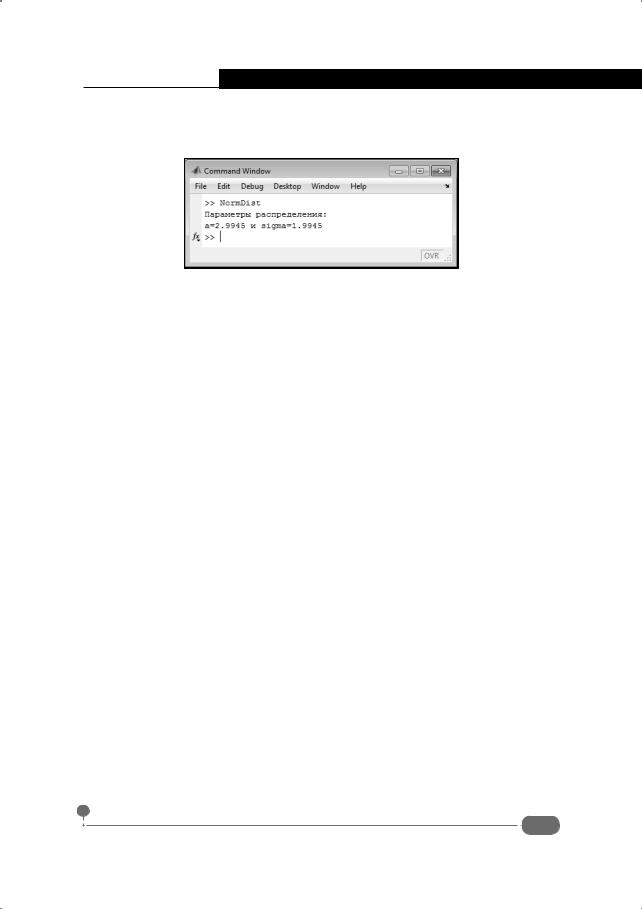
Сохраняем командный код в файле с именем NormDist.m. В командном окне выполняем команду NormDist. Результат показан в документе на рис. 8.27.

Рис. 8.27. Результаты вычислений

Вычисленные значения достаточно близки к теоретическим. В принципе, увеличение объема выборки повышает точность. Тем не менее, следует помнить, что речь идет об обработке статистических данных, поэтому даже очень большой объем выборки не гарантирует стопроцентной достоверности полученных результатов.

347

Глава 9 Символьные вычисления

- Штирлиц, Вы ведь сами учили меня аналитичности и спокойствию.

- Это Вы меня призываете к спокойствию? После того, что сказали?!

К/ф "Семнадцать мгновений весны"

Несмотря на то, что приложение Matlab предназначено для выполнения числовых расчетов, в Matlab также можно выполнять расчеты и в символьном виде – то есть расчеты, в которых используются символьные переменные, а в результате получают символьные (аналитические) выражения. Именно символьным вычислениям посвящена данная глава. Есть несколько способов выполнять вычисления в символьном виде. Один, простой, подразумевает использование специальных встроенных функций в командном окне, второй, тоже простой, подразумевает использование специального пакета инструментов (который называется Symbolic Math Toolbox).

Использование символьных переменных

Я должен Вас поздравить, Ватсон. Вы сделали, в общем, правильные наблюдения. Вы ошиблись только в знаке.

К/ф "Приключения Шерлока Холмса и доктора Ватсона. Знакомство"

В первую очередь рассмотрим способы ввода в рабочем документе (командном окне) символьных переменных – переменных, значениями которых являются их названия. Другими словами, символьной переменной значение не присваивается. Проблема в том, что если просто попытаться воспользоваться переменной, которой не присвоено значение, появится сообщение об ошибке. Поэтому необходимо предпринять некоторые предосторожности. Предосторожности состоят в том, что символьные переменные предварительно необходимо объявить, для чего используем ключевое слово syms. После этого ключевого слова указываются, через пробел, те переменные, которые необходимо рассматривать как символьные. Если впоследствии эти переменные используются в выражениях, то результат также получим символьный. Пример использования символьных переменных приведен в документе на рис. 9.1.

Документ любопытный, и имеет смысл рассмотреть его подробно. Первой командой в документе является инструкция syms a b c, которой

348

Глава 9. Символьные вычисления

Рис. 9.1. Использование символьных переменных

объявляются три символьные переменные: a, b и c. Затем командой x=(-b+sqrt(b^2-4*a*c))/2/a переменной x присваивается значение, представленное в виде выражения, содержащего символьные переменные. Таким образом, переменная x получает символьное значение. Значение этой переменной так и отображается, в терминах переменных a, b и c в командном окне. Чтобы увидеть значение переменной x в более наглядном виде, используем функцию pretty(), аргументом которой указывается символьное значение (в данном случае – переменная x). Переменную x в свою очередь также можно использовать в дальнейших вычислениях. Например, переменной eq значение присваивается командой eq=a*x^2+b*x+c. Здесь отметим, что присвоенное переменной x значение определяется выражени-

349

Самоучитель Matlab

ем x = −b + b2 − 4ac , которое, в свою очередь, есть не что иное, как один

2a

из корней уравнения ax2 +bx +c = 0 . Поэтому значение переменной eq должно с неизбежностью равняться нулю. Но убедиться в этом не просто. При вычислении значения этой переменной получаем символьное выражение, в котором сложно узнать ноль. Не помогает и команда pretty(eq). Ситуация проясняется, если воспользоваться командой simplify(eq). Функцией simplify() упрощается выражение, указанное аргументом.

Вданном случае после упрощения получаем ноль, как и следовало ожидать.

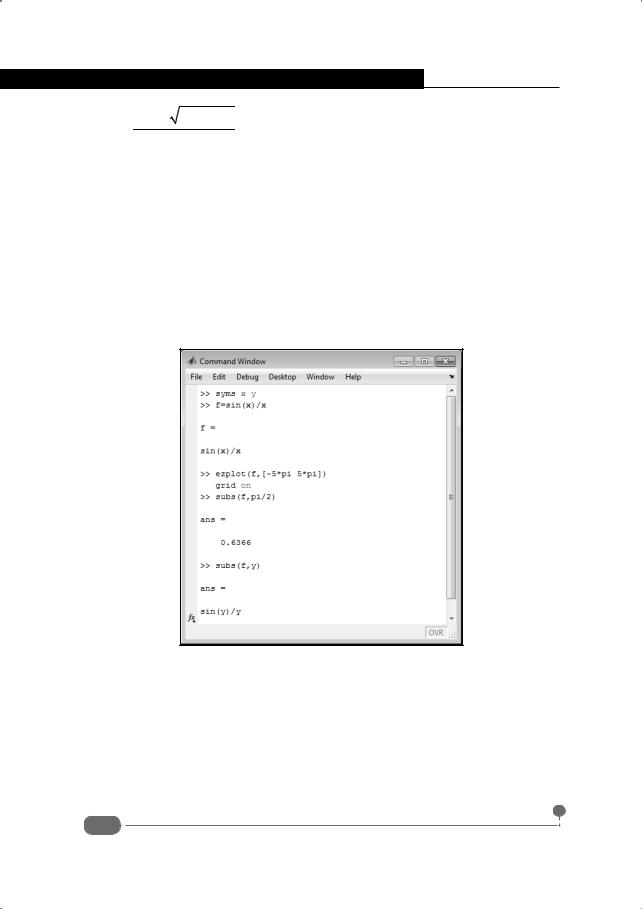
Всимвольном виде удобно задавать функции. Для этого аргумент (или аргументы) функции предварительно объявляется как символьная переменная, после чего функция задается как выражение, зависящее от этой переменной. Такой простой пример приведен в документе на рис. 9.2.

Рис. 9.2. Функция задана через символьную переменную

Правда, вычисление таких функций имеет некоторые особенности. Например, командой syms x y определяем две символьные переменные. Затем командой f=sin(x)/x на основе символьной переменной x задаем значение переменной f. После этого переменную f можно использовать для отображения на графике соответствующей функциональной зависимости. Так, результат выполнения команд ezplot(f,[-5*pi 5*pi]) и grid on показан на рис. 9.3.

350