1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 5. Решение уравнений и оптимизация

Предварительно в редакторе m-файлов вводится следующий код для функции, определяющей решаемое уравнение (оно такое же, как в предыдущем случае):

function z=f(x) z=2*sin(x)^2+sin(x)-1; end

Окно редактора m-файлов с этим кодом представлено на рис. 5.3.

Рис. 5.3. Код функции в окне редактора m-файлов

Для решения уравнения с передачей ссылки на функцию двумя разными способами используем такой код:

>>z=fzero(@f,pi/4)

z =

0.5236

>>z=fzero('f',3*pi/4)

z =

2.6180

Вкоманде z=fzero(@f,pi/4) первым аргументом функции fzero() передается указатель на функцию. Для получения указателя перед именем функции указываем инструкцию @, в результате получаем @f. Вто-

рым аргументом указывается начальное приближение для корня уравнения pi/4. Это означает, что корень ищется в окрестности точки π 4 .

Врезультате находим (в числовом виде) корень x = π 6 . В команде z=fzero('f',3*pi/4) в качестве ссылки на функцию передается имя файла, в котором описана функция, определяющая уравнение. В качестве

начального для поиска корня здесь указано значение 3*pi/4. Как результат, находится корень x = 5π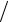6 .

На заметку

Из того, что мы ищем корень в окрестности какой-то точки, еще не означает, что именно в окрестности этой точки будет найдено решение. Более того, нет гарантии, что вообще будет найдено хоть какое-то решение.

201

Самоучитель Matlab

При вызове функции fzero() можно узнать не только корень уравнения, но и ряд других параметров. В частности, помимо корня, в качестве результата функцией fzero() возвращается значение функции, определяющей уравнение, для найденного корня.

На заметку

Кроме того, дополнительными параметрами в результате возвращаются: статус результата вычисления корня, использованный алгоритм, количество итераций и так далее.

Еще один пример использования функции fzero() приведен в документе на рис. 5.4.

Рис. 5.4. Функцией fzero() возвращается корень и значение функции в этой точке

Основу кода составляют две команды, которые рассмотрим по отдельности. Первой командой F=@(x)(sin(x)+cos(x)) задается функция F(x) = sin(x) + cos(x). Специфика этой команды в ее синтаксисе. Такой синтаксис используется для объявления анонимных функций. Общий синтаксис такой: инструкция @, в круглых скобках список аргументов, а в следующей паре круглых скобок указывается выражение, определяющее функцию, то есть @(аргументы)(выражение). Если такую конструкцию присвоить в качестве значения переменной, то эта переменная будет указателем на соответствующую функцию. Собственно, этим правилом мы

ивоспользовались при определении функции для уравнения.

На заметку

Пожалуй, главное преимущество в использовании анонимных функций состоит в том, что с их помощью функции можно объявлять прямо в командном окне.

202

Глава 5. Решение уравнений и оптимизация

Еще одна команда, которую мы использовали, – это [z,res]= fzero(F,[0 pi]). Думается, аргументы функции fzero() особых вопросов не вызовут. А результат вызова функции fzero() записывается в две переменные: переменная z в качестве значения получает корень уравнения (на интервале от 0 до π - это значение x = 3π4 ), а в переменную res записывается значение функции F() в точке - корне уравнения.

На заметку

Если корень уравнения найден точно, то значение функции уравнения в точке должно равняться нулю. Обычно значение корня является приближенным, поэтому и функция в соответствующей точке отличается от нуля. Чем ближе значение функции уравнения в найденной точке решения, тем точнее вычислен корень. Тем не менее, не следует путать точность вычисления корня с отклонением функции уравнения от нулевого значения в найденной точке решения.

Для решения систем уравнений (или отдельных уравнений) используют функцию fsolve(). Принципиальное отличие функции fsolve() от fzero() состоит в том, что первым аргументом функции fsolve()можно передавать ссылку не только на скалярную, но и на векторную функцию. Именно это обстоятельство позволяет решать с помощью функции fsolve() системы дифференциальных уравнений. Все способы вызова функции fsolve() здесь рассматривать не будем. Ограничимся лишь основными. Обратимся к примерам. Начнем с отдельного (скалярного уравнения). Соответствующий документ представлен на рис. 5.5.

Командный код имеет следующий вид (для удобства команды пользователя выделены жирным шрифтом, а текстовое сообщение, выводимое в результате вычисления корня, выделено курсивом):

>>F=@(x)(2*sin(x)^2+sin(x)-1);

>>[x,res]=fsolve(F,pi/5)

Equation solved.

fsolve completed because the vector of function values is near zero as measured by the default value of the function tolerance, and the problem appears regular as measured by the gradient.

<stopping criteria details> x =

0.5236 res =

8.2934e-013

Командой F=@(x)(2*sin(x)^2+sin(x)-1) непосредственно в командном окне задается функциональная зависимость F(x) = 2 sin(x)2 + sin(x) −1 . Уравнение 2 sin(x)2 + sin(x) −1 = 0 решаем командой [x,res]=fsolve (F,pi/5). Здесь первым аргументом функции fsolve(F,pi/5) передается указатель на функцию, определяющую решаемое уравнение. Второй

203

Самоучитель Matlab

Рис. 5.5. Решение скалярного уравнения с помощью функции fsolve()

аргумент – начальное приближение для корня уравнения. Результат возвращается в виде значения корня уравнения (переменная z) и значения функции уравнения в найденном корне (переменная res). Помимо непосредственно результатов вычислений функцией fsolve() выводится текстовое сообщение с пояснениями, насколько успешно прошли вычисления

ипочему функция fsolve() завершила работу.

На заметку

Функция завершает работу, если корень, удовлетворяющий определенным критериям, найден или если, например, функция не может найти корень. Иногда формальное решение найдено, но нет уверенности, что это правильное решение. Эту и другую полезную информацию можно получить из текстового сообщения.

Как отмечалось выше, важным преимуществом функции fsolve() является то, что с ее помощью можно решать системы уравнений. Для этого необходимо создать векторную функцию, которая описывает систему уравнений, и передать ее первым аргументом функции fsolve(). Вторым аргументом передается список начальных значений по каждой из переменных, относительно которых решается уравнение. Рассмотрим простой пример (рис. 5.6).

204

Глава 5. Решение уравнений и оптимизация

Рис. 5.6. Решение системы уравнений

Сначала командой F=@(x)[(x(1)^2+x(2)^2-25),((x(1)+1)*x(2)- 16)] задается вектор-функция из двух элементов. Эта вектор-функция определяет решаемую систему уравнений. Определяем ее в командном окне в виде указателя на анонимную функцию.

На заметку

Анонимную вектор-функцию в командном окне мы определяем так. Сначала, как обычно, указывается инструкция @, затем в круглых скобках один (векторный!) аргумент и затем две функциональные зависимости, реализованные в виде вектор-столбца. Для этого в квадратных скобках указывается два выражения, разделенные точкой с запятой. Векторный аргумент функции обозначен как x. Поскольку вектор-функция состоит из двух элементов, то вполне логично, что аргумент x также состоит из двух элементов (количество уравнений в системе должно равняться количеству неизвестных, относительно которых решается система). Поэтому ссылки на неизвестные переменные, относительно которых решается система уравнений, имеют вид x(1) и x(2). Именно эти ссылки используются в выражениях для элементов вектор-функции.

В соответствии с теми выражениями, которые указаны при определе-

нии вектор-функции, решается система уравнений x12 + x22 −25 = 0 и x1x2 −12 = 0 . У этой системы есть точное решение x1 = 3 и x2 = 4 . Это решение и пытаемся найти. Чтобы поиск был удачным, желательно указать начальную точку как можно ближе к точке решения. Мы выбираем в качестве начальной точку x1 = 0 и x2 = 1.

205

Самоучитель Matlab

На заметку

Поскольку в общем случае решение неизвестно, то задача выбора начальной точки также представляется нетривиальной. С другой стороны, нередко успех в поиске решения системы уравнений принципиально зависит от того, насколько удачно выбрано начальное приближение. Для этого иногда приходится проводить дополнительное исследование, более объемное, чем сама процедура поиска решения.

Чтобы решить систему уравнений, используем команду z=fsolve (F,[0 1]). В результате получаем текстовое сообщение о результатах поиска решения и непосредственно результат вычислений в виде списка из двух элементов. Список присваивается в качестве значения переменной z. Элементы списка – решение системы уравнений. Как видим, это именно то решение, которое мы ожидали получить.

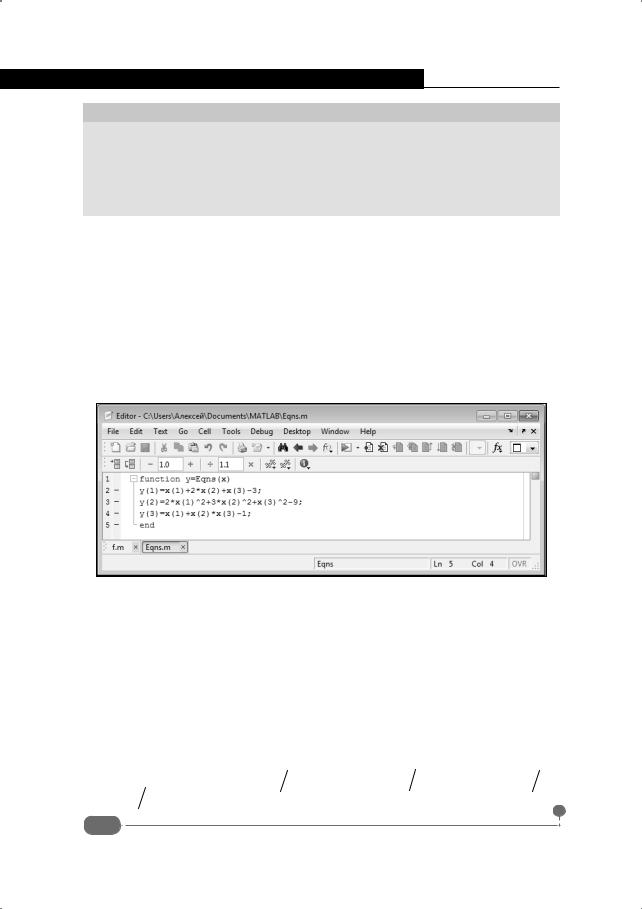
Разумеется, при решении системы уравнений вектор-функцию, определяющую уравнения системы, можно реализовать не только в командном окне, но и в m-файле. Рассмотрим программный код, представленный в документе на рис. 5.7.

Рис. 5.7. Программный код вектор-функции

Этим кодом определяется вектор-функция из трех элементов:

function y=Eqns(x) y(1)=x(1)+2*x(2)+x(3)-3; y(2)=2*x(1)^2+3*x(2)^2+x(3)^2-9; y(3)=x(1)+x(2)*x(3)-1;

end

Эта вектор-функция соответствует следующей системе алгебраиче-

206

Глава 5. Решение уравнений и оптимизация

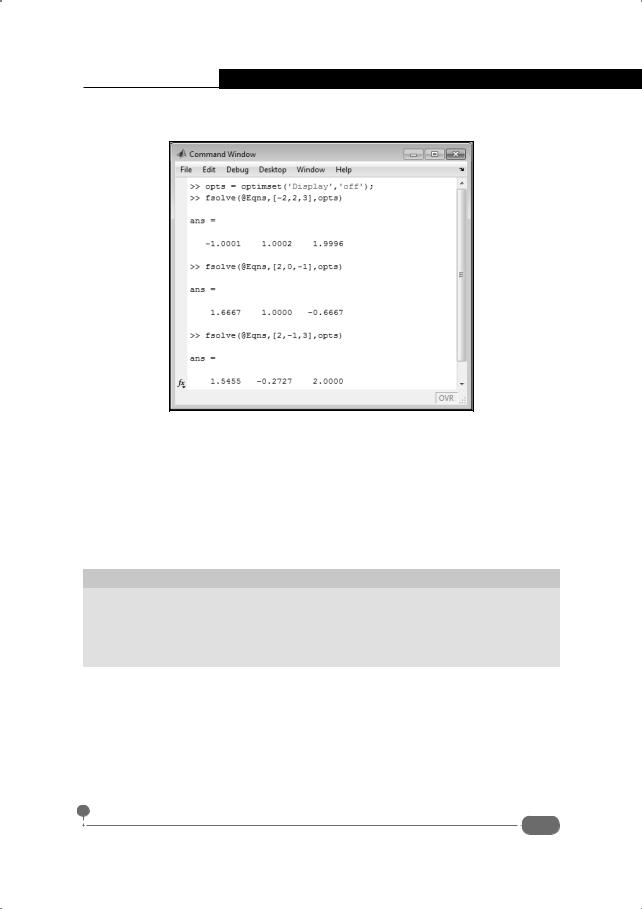
fsolve() и вектор-функции, определенной выше. Документ представлен на рис. 5.8.

Рис. 5.8. Поиск всех корней системы уравнений

Кроме обычных параметров функции fsolve() в данном случае используются дополнительные настройки, отменяющие режим вывода текстовой информации о результатах вычислений. Для этого используем команду opts=optimset('Display','off'). Затем в команде fsolve (@Eqns,[-2,2,3],opts) переменная opts указывается третьим аргументом функции fsolve(). В результате решение системы уравнений вычисляется, а текстовое сообщение не выводится.

На заметку

Дополнительные параметры для функции fsolve() задаются с помощью функции optimset() в обычном для Matlab формате – в одинарных кавычках указывается опция и через запятую ее значение. Результат вызова функции optimset() записывается в переменную, которая затем передается аргументом другой функции – например, функции fsolve().

Передавая разные начальные значения для поиска корней системы уравнений, получаем разные решения. Это иллюстрация к тому, как важно удачно выбрать начальное приближение для поиска решения.

Еще одна полезная функция, на которую хочется обратить внимание, позволяет находить корни полиномов. Напомним, что по-

207

Самоучитель Matlab

тура полинома жестко фиксирована, для его вычисления достаточно знать значение переменной x и коэффициенты a1 , a2 ,...,an +1 . Если же речь идет о полиноме как о функциональной зависимости, то набора коэффициентов a1 , a2 ,...,an +1 достаточно для однозначного определения соответствующей функции. Если речь заходит об обработке полинома в Matlab, то, как правило, речь идет о списке коэффициентов полинома. Это простой, экономный

иэффективный подход.

На заметку

Если полином степени n , то для его однозначного определения необходимо указать n +1 коэффициент, то есть на единицу больше, чем степень полинома. Коэффициенты в списке необходимо указывать все, в том числе и нулевые. Положение коэффициента в списке определяет степень соответствующего слагаемого. Корнями полинома называются решения уравнения Pn(x) = 0 .

Для вычисления корней полинома используют функцию roots(). Аргументом указывается список коэффициентов полинома. Результатом возвращается список корней полинома. Пример представлен в документе на рис. 5.9.

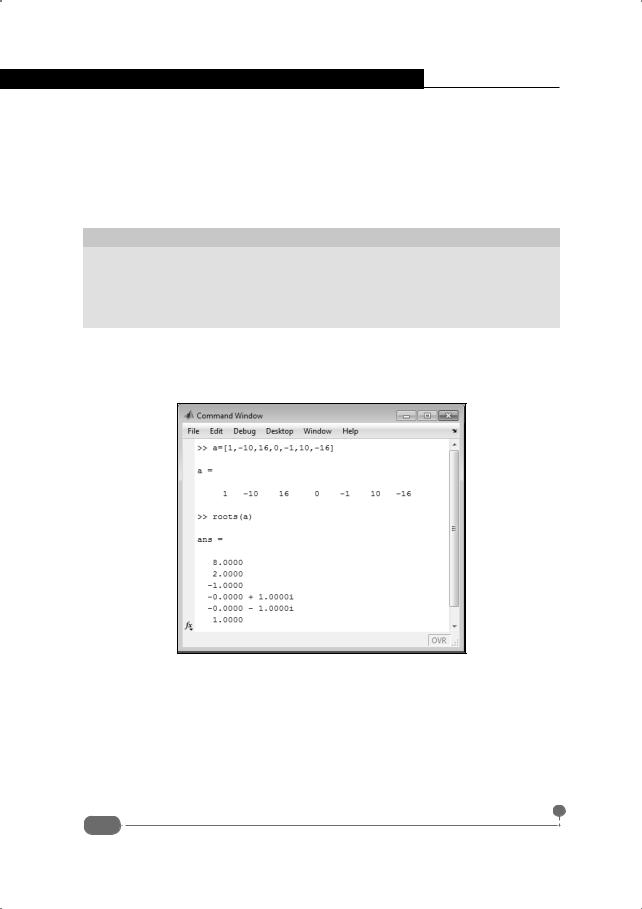
Рис. 5.9. Вычисление корней полинома

Сначала командой a=[1,-10,16,0,-1,10,-16] создаем список коэффициентов полинома. Эти коэффициенты соответствуют полиному шестой степени P6(x) = x6 −10x5 +16x4 −x2 +10x −16 . У полинома есть четыре действительных корня x = −1 , x = 1 , x = 2 , x = 8 и два комплексных x = i и x = −i (здесь i - мнимая единица: i2 = −1 ). Вычислить эти корни можно с помощью команды roots(a). В результате появляется список корней, в том числе и комплексных (см. рис. 5.9).

208

Глава 5. Решение уравнений и оптимизация

Вычисление корней уравнений в явном виде

Мы, конечно, все что можно, со своей стороны делаем, но не все мы можем. То есть мы можем, но совесть нам не позволяет.

Б. Ельцин

Несмотря на наличие встроенных функций, иногда полезно писать процедуру поиска решений уравнения или системы уравнений в явном виде. В этом разделе рассмотрим наиболее простые методы решения уравнений и систем.

Простой и надежный метод решения уравнений – метод половинного деления. Метод используется для поиска корня уравнения f (x) = 0 на интервале значений аргумента от a до b . Необходимое условие для применимости метода (кроме непрерывности функции f (x)) состоит в том, чтобы функция f (x) принимала на границах интервала значения разных знаков, что математически можно записать в виде неравенства f (a)f (b) ≤ 0 . В этом случае на интервале поиска гарантированно находится, по крайней мере, один корень уравнения.

На заметку

Суть метода состоит в следующем. В центре интервала, на котором ищется корень, вычисляется значение функции. Интерес представляет знак вычисленного значения, поскольку в центр интервала перемещается та граница, для которой знак значения функции совпадает со знаком значения функции в центре. В результате за одну итерацию интервал поиска уменьшается вдвое.

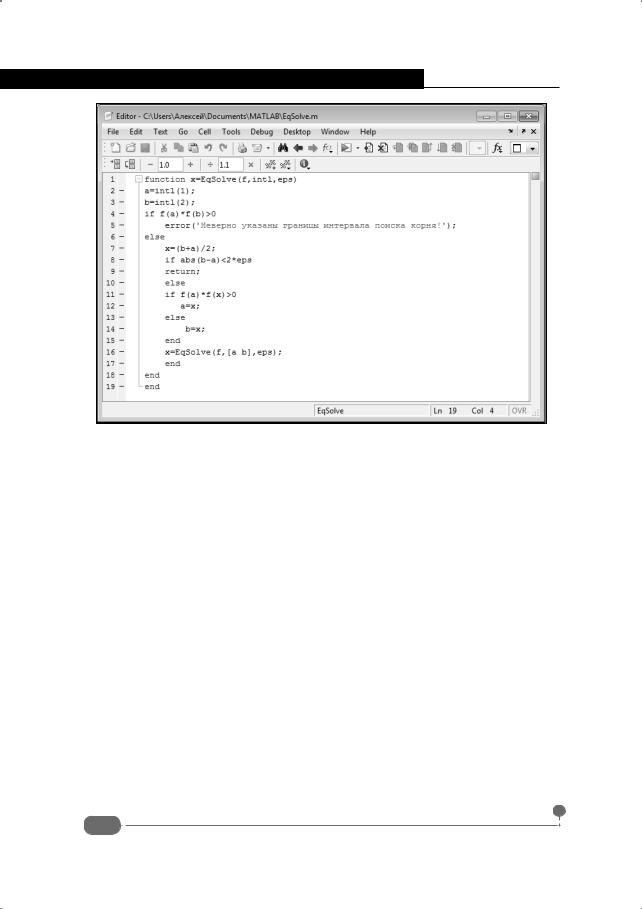
На рис. 5.10 показан документ с кодом функции, предназначенной для решения уравнений методом половинного деления.

Код функции EqSolve() состоит из группы вложенных условных операторов. В нем также используется рекурсия. Проанализируем этот код:

function x=EqSolve(f,intl,eps) a=intl(1);

b=intl(2);

if f(a)*f(b)>0

error('Неверно указаны границы интервала поиска корня!'); else

x=(b+a)/2;

if abs(b-a)<2*eps return;

else

if f(a)*f(x)>0 a=x;

209

Самоучитель Matlab

Рис. 5.10. Окно редактора m-файлов с кодом функции для решения уравнений методом половинного деления

else b=x;

end

x=EqSolve(f,[a b],eps); end

end end

У функции три аргумента: указатель на функцию f, которая определяет решаемое уравнение, интервал поиска решения intl, а также точность вычисления корня eps. В качестве результата функцией возвращается значение корня уравнения. Результат записывается в переменную, которая в коде обозначена как x.

Командами a=intl(1) и b=intl(2) считываются элементы списка intl и запоминаются в переменных a и b. После этого в условном операторе проверяется условие f(a)*f(b)>0. Если это условие выполняется, то функция на границах интервала поиска решения принимает значения одинаковых знаков. В этом случае командой error('Неверно указаны границы интервала поиска корня!') выводится сообщение о том, что границы диапазона для поиска решения указаны неверно. Если условие f(a)*f(b)>0 не выполняется, можно начинать поиск решения. Начина-

210