1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 4. Элементы матричной алгебры

На заметку

Строго говоря, для вычисления скалярного произведения первый вектор должен быть вектором-строкой, а второй – вектором-столбцом. Мы от таких тонкостей абстрагируемся.

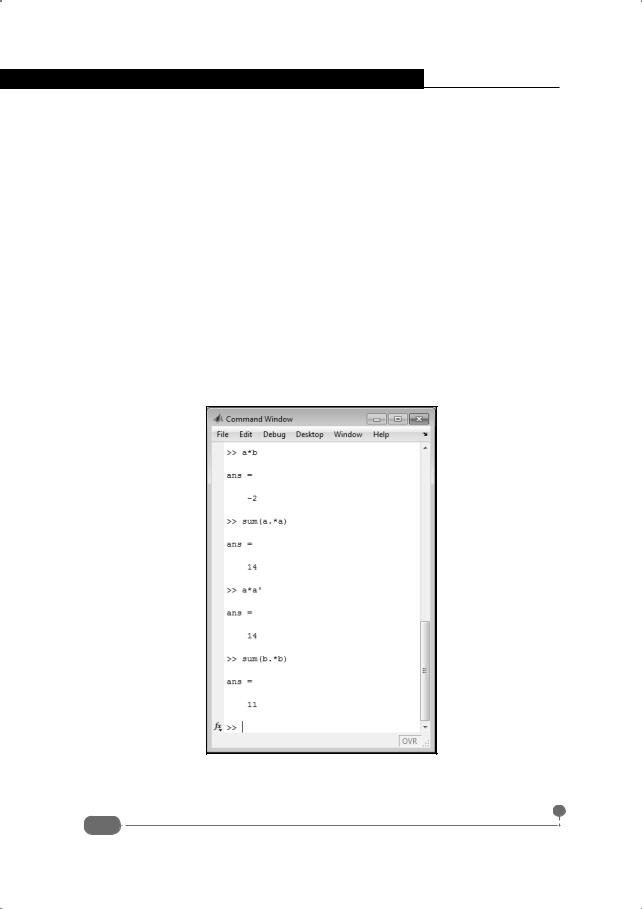
Вычислить скалярное произведение можно с помощью функции dot(). Аргументы функции – векторы, для которых вычисляется скалярное произведение. Примеры приведены в документе на рис. 4.2.

Рис. 4.2. Вычисление скалярного произведения

Операция вычисления скалярного произведения коммутативна – аргументы функции dot() можно указывать в произвольном порядке. Здесь мы использовали такой код:

>>a=[1 -2 3];

>>b=[3;1;-1];

>>dot(a,b)

151

Самоучитель Matlab

ans = -2

>>dot(b,a) ans =

-2

>>dot(a,a) ans =

14

>>dot(b,b) ans =

11

Стоит обратить внимание на два обстоятельства. Во-первых, один из векторов является строкой, а второй – столбцом. Вне зависимости от того, как передаются эти векторы аргументами функции dot(), результат вычисляется один и тот же. Во-вторых, если вычислить скалярное произведение вектора на себя же, получим квадрат модуля этого вектора.

Достаточно просто скалярное произведение вычисляется и без использования функции dot().

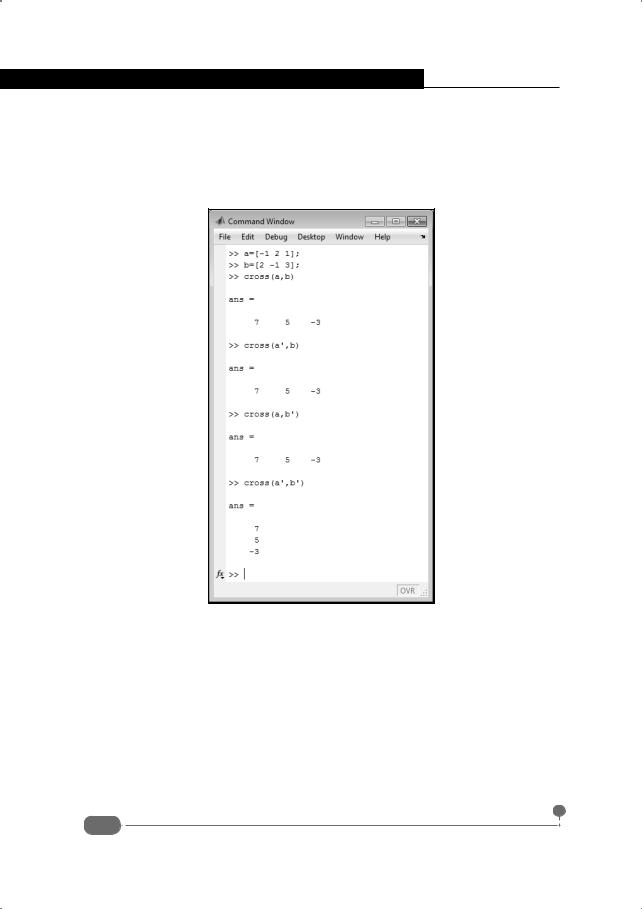
Рис. 4.3. Альтернативный способ вычисления скалярного произведения

Соответствующий программный код приведен ниже:

152

Глава 4. Элементы матричной алгебры

>>a*b ans =

-2

>>sum(a.*a) ans =

14

>>a*a'

ans = 14

>> sum(b.*b) ans =

11

Так, значение переменной a есть вектор-строка, а значением переменной b является вектор-столбец. Скалярное произведение можно вычислить командой a*b. Здесь, фактически, речь идет о произведении двух матриц (см. далее). В соответствии с правилом вычисления произведения матриц принципиально важно, чтобы количество столбцов первой матрицы равнялось количеству строк второй матрицы. В отношении векторов это означает, что первый вектор - это вектор-строка, а второй – вектор-столбец.

В результате выполнения команды a.*a получаем массив, элементы которого равны попарным произведениям соответствующих элементов первого и второго вектора, то есть квадратам элементов вектора a. Чтобы получить скалярное произведение (квадрат модуля вектора), используем функцию sum(). Другой способ получить тот же результат – воспользоваться командой a*a'. Здесь мы командой a' транспонировали вектор-строку, получив в результате вектор-столбец. Поэтому мы этот вектор можем умножить (указав его вторым в произведении) на вектор-строку a.

Команда sum(b.*b) вычисляется по тому же принципу, что и команда sum(a.*a), только теперь речь идет о векторах-столбцах.

Еще одна важная операция, которую достаточно часто приходится выполнять, связана с вычислением векторного произведения.

2 и 3, причем имеет место циклическая "перестановка" индекса. То есть, например, если k = 3 , то формальное значение k +1 = 4 следует заменить на 1, а значение k + 2 = 5 следует заменить на 2.

153

Самоучитель Matlab

Векторное произведение вычисляется с помощью функции cross(). Аргументами указываются векторы, для которых вычисляется векторное произведение. Векторы могут быть как строками, так и столбцами. Если среди аргументов есть вектор-строка, то результатом также будет вектор-строка. Если оба вектора являются столбцами, то результатом будет вектор-столбец. Примеры вызова функции cross() приведены в документе на рис. 4.4.

Рис. 4.4. Вычисление векторного произведения

Для удобства ниже приведен соответствующий программный код (жирным шрифтом выделен ввод пользователя):

>>a=[-1 2 1];

>>b=[2 -1 3];

>>cross(a,b) ans =

7 5 -3 >> cross(a',b) ans =

7 5 -3

154

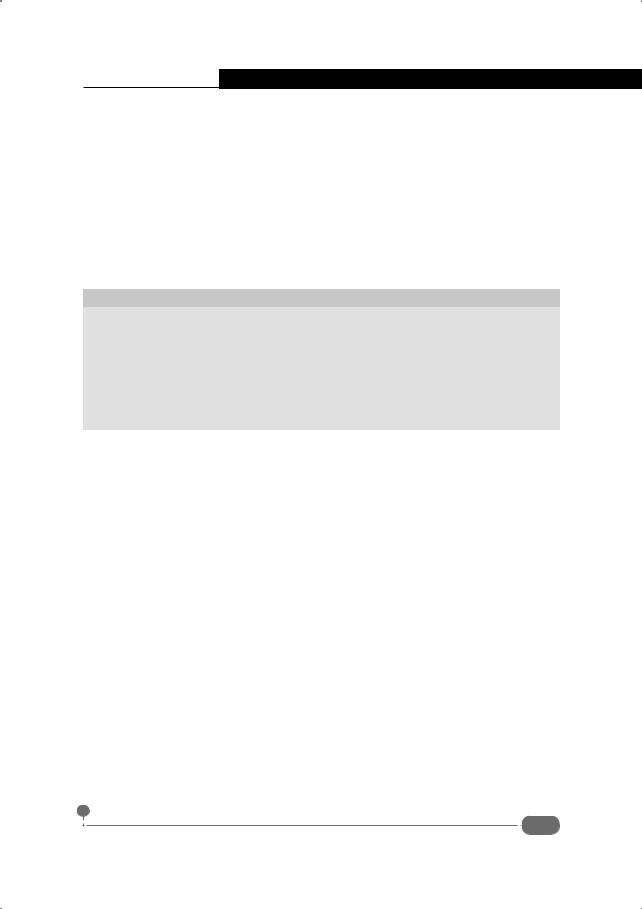
Глава 4. Элементы матричной алгебры

>> cross(a,b') ans =

7 5 -3 >> cross(a',b') ans =

7

5 -3

Думается, что особых комментариев этот код не требует. Единственное, на

что стоит обратить внимание, – это то, что векторное произведение анти-

коммутативно, то есть b ×a = −a ×b .

На заметку

Есть еще такие тривиальные операции, как умножение/деление вектора на число или вычисление суммы/разности векторов. В этом случае правила достаточно простые. При умножении/делении вектора на число с помощью соответственно оператора * или / операция выполняется с каждым элементом вектора, то есть в соответствии с правилом умножения/деления вектора на число. Складываются и вычитаются векторы посредством операторов + и -. В этом случае необходимо, чтобы векторы-операнды имели одинаковый размер и были одного типа (оба векторы-столбцы или векторы-строки).

Операции с матрицами

- Эти сведения недорого стоят. - Ну, какие есть.

К/ф "Клуб самоубийц, или Приключения титулованной особы"

Среди наиболее важных задач, относящихся к работе с матрицами, можно выделить такие: вычисление детерминанта (определителя) матрицы, вычисление собственных значений и собственных векторов матрицы, обращение матрицы (вычисление обратной матрицы), транспонирование матрицы, умножение матриц, вычисление функций с матричными аргументами. Рассмотрим, как эти задачи решаются средствами Matlab. Начнем с произведения матриц.

Для вычисления произведения матриц используется стандартный оператор произведения *. Если операндами этого бинарного оператора являются матрицы, то произведение вычисляется по правилам вычисления матричного произведения. Необходимым условием является равенство количества столбцов первой матрицы и строк второй. Это автоматически означает, что произведение можно вычислить далеко не для всех матриц. Часто приходится иметь дело с квадратными матрицами, у которых количество строк равняется количеству столбцов. В этом случае можно множить матрицы

155

Самоучитель Matlab

одинаковых размеров. Так, если ˆ и ˆ – квадратные матрицы одного раз-

A B

результат вычислений в общем случае различный. То есть свойством коммутативности матричное произведение не обладает.

На заметку

k =1

условии, что индексы принимают значения i = 1,2,..,m и j = 1,2,...,n .

В результате матричного произведения получаем матрицу. Количество строк матрицы определяется количеством строк в первой матрице. Количество столбцов определяется количеством столбцов во второй матрице.

На заметку

Поэтому при вычислении произведения вектора-строки на вектор-столбец получаем скаляр: это матрица, которая состоит из одной строки одного столбца.

Пример вычисления матричного произведения приведен в документе на рис. 4.5.

В командном окне представлен такой код (жирным шрифтом выделен ввод пользователя):

>> A=[1 -2 3 -1;0 -2 1 2;-2 1 1 0]

A =

>> B=[1 2;-2 1;0 -1;1 0]

B =

12

-2 1

0-1

10

>>C=A*B

C =

Исходные матрицы имеют размеры 3×4 и 4×2, поэтому матрица-результат имеет размер 3×2.

156

Глава 4. Элементы матричной алгебры

Рис. 4.5. Произведение матриц

На заметку

Результатом произведения двух квадратных матриц размера n ×n является квадратная матрица размера n ×n .

Достаточно тривиальной является процедура транспонирования матрицы. При транспонировании матрица-результат получается из исходной матрицы взаимной заменой строк и столбцов: первая строка исходной матрицы становится первым столбцом матрицы-результата, вторая строка исходной матрицы становится вторым столбцом матрицы-результата и так далее. В Matlab для выполнения операции транспонирования используется оператор .' (или оператор ' для действительных матриц).

На заметку

Оператор ' используется для вычисления сопряженной матрицы, которая получается из исходной транспонированием и комплексным сопряжением ее элементов. Поскольку мы будем использовать в основном матрицы действительные, то процедура сопряжения совпадает с процедурой транспонирования. Вообще же для транспонирования используется составной оператор .'.

157

Самоучитель Matlab

Если к матрице C из предыдущего примера, где вычислялось матричное произведение, применить процедуру транспонирования, получим результат, как на рис. 4.6.

Рис. 4.6. Транспонирование матрицы

Для вычисления суммы или разности матриц они должны быть одинакового размера. При умножении или делении матрицы на число эта операция применяется к каждому элементу матрицы. В качестве иллюстрации рассмотрим такой код:

>> A=[1 2 3;-2 -1 0]

A =

1 2 3 -2 -1 0

>> B=[0 -1 2;1 -1 2]

B =

Этим кодом вычисляется линейная

Результат получается так. Каждый

элемент матрицы ˆ умножается на

A

2. От элементов полученной матрицы отнимаются соответствующие

элементы матрицы ˆ, предвари-

B

тельно умноженные на 3 (рис. 4.7).

Определитель, или детерминант,

вычисляется только для квадрат- Рис. 4.7. Линейная комбинация матриц

158

Глава 4. Элементы матричной алгебры

ных матриц. Это число. Методику его вычисления проще всего описать через рекурсивную процедуру. Так, для матрицы размерами 2×2 детерминант вычисляется как разность произведений диагональных и недиагональных эле-

и j -го столбца. Уже отсюда совершенно очевидно, что вычислять детерминант матрицы лучше с помощью специальных, предназначенных для этой цели, функций, которые в Matlab, к счастью, имеются. В частности, детерминант вычисляется с помощью функции det(). Аргументом функции указывается матрица, для которой вычисляется детерминант. Пример вычисления детерминанта матрицы приведен в документе на рис. 4.8.

Рис. 4.8. Вычисление детерминанта матрицы

Если детерминант матрицы отличен от нуля, такая матрица называется невырожденной. Для невырожденной матрицы может быть вычислена обратная матрица. По определению обратной к невырожденной матрице

ˆ называется такая матрица (обычно обозначается ˆ−1), которая, будучи

A A

умноженной на матрицу ˆ, дает единичную матрицу (по диагонали едини-

A

цы, а все прочие элементы равны нулю). Для вычисления обратной матри-

159

Самоучитель Matlab

цы в Matlab используется функция inv(), аргументом которой указывается матрица, для которой нужно вычислить обратную. Пример вычисления обратной матрицы приведен в документе на рис. 4.9.

Рис. 4.9. Вычисление обратной матрицы

Мы использовали такую последовательность команд (жирным шрифтом выделен ввод пользователя):

>> A=[1 2 1;-1 0 1;2 -1 1]

A =

>> B=inv(A)

B =

160