1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 3. Элементы программирования

тинном условии выполняется блок команд до следующего ключевого слова elseif. Если условие условие_2 ложно, проверяется условие_3, и так далее. В случае, если ни одно из условий не выполнено, выполняются команды после ключевого слова else. Далее приведен пример программного кода, в котором используются условные операторы:

function y=MakeChoice(x) if x<0

disp('Отрицательное значение аргумента!');

else

disp('Неотрицательное значение аргумента!');

end

disp('Вычисление значения функции:'); if x<-5

y=x+5; elseif x<0

y=x*(x+5); elseif x<7

y=x*(x-7);

else

y=x-7;

end

disp('Вычисление значения функции завершено!'); if y==0

disp('Значение функции равно нулю!');

end end

Окно редактора m-файлов с этим кодом представлено на рис. 3.21.

Код функции MakeChoice() несколько искусственный и носит иллюстративный характер. Основу его составляют три условных оператора. В первом из них проверяется условие x<0, где через x обозначен аргумент функции. Условие x<0 является истинным, если аргумент функции меньше нуля.

Вэтом случае на экран выводится сообщение о том, что у функции отрицательный аргумент. В противном случае, то есть если условие x<0 ложно, выводится сообщение о том, что аргумент неотрицательный.

Вследующем условном операторе проверяется условие x<-5. Если это так, то переменной y, которая предназначена для записи значения функции, присваивается значение x+5. Если условие x<-5 не выполнено, проверяется условие x<0. В этом случае выполняется команда y=x*(x+5). Если же не выполнено и условие x<0, проверяется условие x<7. На этот случай, то есть когда аргумент функции меньше семи (но не меньше нуля), предусмотрена команда y=x*(x-7). Если ни одно из перечисленных условий не выполняется (аргумент функции больше либо равен семи), значение переменной y определяется с помощью команды y=x-7.

121

Самоучитель Matlab

Рис. 3.21. Программный код функции MakeChoice() с использованием условных операторов

После того, как вычислено значение функции (присвоено значение переменной y), выполняется еще один условный оператор, в котором проверяется условие равенства нулю значения функции (условие y==0). Если условие выполнено, выводится текстовое сообщение о том, что значение функции нулевое. В противном случае никаких дополнительных действий не предпринимается. Результат вызова функции MakeChoice() с разными аргументами приведен на рис. 3.22.

На заметку

Стоит обратить внимание на второй условный оператор с несколькими проверяемыми условиями. Особенность его состоит в том, что каждое следующее условие проверяется только в том случае, если не выполнено ни одно из предыдущих условий.

Подобно условному оператору if, в котором проверяется серия условий, с помощью оператора перебора switch выполняется проверка значения переменной или выражения. Переменная указывается после ключевого слова switch. Ключевое слово case используется для организации программных блоков, которые выполняются в зависимости от значения переменной. Общий синтаксис вызова оператора перебора switch следующий:

122

Глава 3. Элементы программирования

Рис. 3.22. Результат вычисления функции MakeChoice() для разных аргументов

switch выражение case значение_1 команды_1

case значение_2 команды_2

...

case значение_N команды_N otherwise

команды_N+1 end

123

Самоучитель Matlab

Оператор выполняется по следующей схеме: вычисляется значение выражения. Затем это значение последовательно сравнивается со значениями, указанными в case-блоках (после ключевого слова case), до первого совпадения. Если совпадение найдено, выполняются команды в соответствующем case-блоке. Если совпадения не найдено, выполняется блок команд, помеченный инструкцией otherwise. Последний блок (то есть otherwise-блок) не является обязательным. Пример использования оператора перебора switch приведен ниже:

function y=MultiFunc(x,n) switch n

case 1 y=x; case 2

y=x*(10-x); case {3,4,5}

y=x*sin(n*x); otherwise

y=1/(1+x^2);

end end

Кодом объявляется функция MultiFunc(), у которой два аргумента. Причем второй аргумент играет роль индикатора, который определяет тип функциональной зависимости. Варианты перебираются с помощью оператора switch. Значение функции записывается в переменную y. При единичном втором аргументе (переменная n) функции MultiFunc() значение переменной y определяется командой y=x в первом case-блоке (через x обозначен первый аргумент функции). Если значение переменной n равно 2, выполняется команда y=x*(10-x). Если же второй аргумент функции MultiFunc() равен 3, 4 или 5, значение функции вычисляется командой y=x*sin(n*x).

На заметку

Обращаем внимание читателя, что в этом случае в качестве проверяемого значения в соответствующем case-блоке указаны фигурные скобки с перечисленными в них значениями 3, 4 и 5 (в качестве разделителя используется запятая).

Наконец, если значение переменной n не совпадает ни с одним из перечисленных выше значений, для определения значения функции выполняется команда y=1/(1+x^2) (блок otherwise). На рис. 3.23 показано окно редактора m-файлов с кодом функции MultiFunc().

124

Глава 3. Элементы программирования

Рис. 3.23. Код функции с оператором перебора

Результат вызова функции MultiFunc() с разными аргументами приведен на рис. 3.24.

Рис. 3.24. Результат вызова функции с оператором перебора

125

Самоучитель Matlab

Кроме условных операторов, имеются операторы цикла for и while. И тот, и другой используются для выполнения последовательности однотипных действий, однако синтаксис у них существенно отличается. В частности, синтаксис вызова оператора цикла for имеет такой вид:

for переменная=значение_1:значение_2:значение_3 команды

end

После ключевого слова for указывается индексная переменная, для которой через знак равенства указывается начальное значение (значение_1), шаг дискретности (значение_2) и конечное значение (значение_3). Начальное значение, шаг дискретности и конечное значение разделяются двоеточиями. Шаг дискретности можно не указывать – в этом случае шаг дискретности единичный.

Выполняется оператор цикла for по следующей схеме: индексная переменная последовательно, с установленным шагом дискретности, пробегает значения от начального до конечного значений, и для каждого из этих значений индексной переменной выполняются команды, вплоть до ключевого слова end, являющегося идентификатором окончания оператора цикла. Далее приведен пример кода, в котором использован оператор цикла for для вычисления суммы ряда:

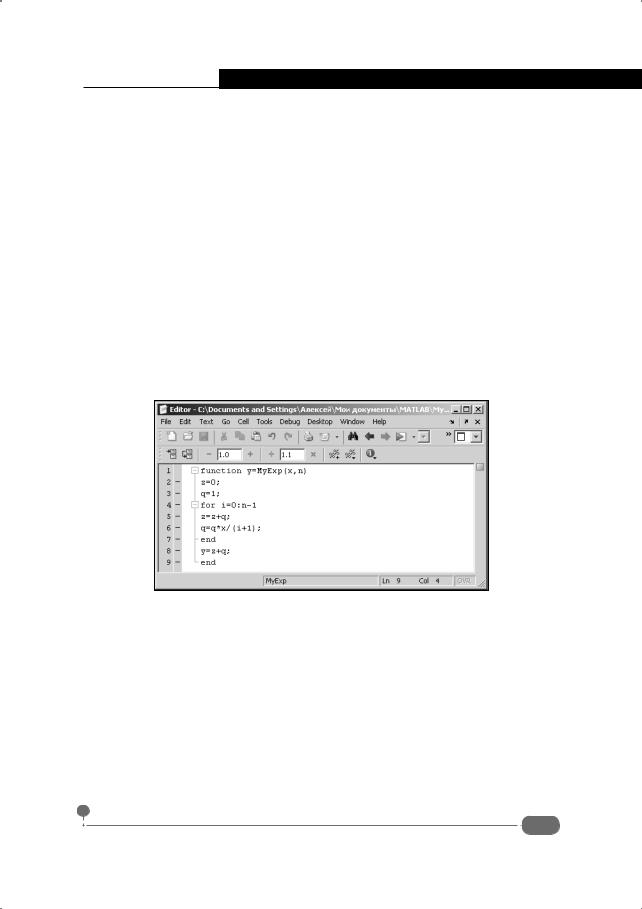
function y=MyExp(x,n) z=0;

q=1;

for i=0:n-1 z=z+q; q=q*x/(i+1); end

y=z+q; end

В коде функции объявляются две локальные переменные (переменная z с начальным нулевым значением и переменная q с начальным единичным значением), а основу кода составляет оператор цикла for. В операторе цикла вводится индексная переменная i с начальным значением 0, конечным значением n-1 (через переменную n обозначен второй аргумент функции MyExp()). Шаг дискретности индексной переменной явно не задан, поэто-

126

Глава 3. Элементы программирования

му по умолчанию он равен единице. На каждом итерационном шаге в операторе цикла выполняется две команды: сначала значение переменной z увеличивается на величину q (команда z=z+q), а затем командой q=q*x/ (i+1) текущее значение переменной q умножается на x (первый аргумент функции MyExp()) и делится на увеличенное на единицу значение индексной переменной. В переменную z записывается сумма ряда, а каждое очередное слагаемое ряда заносится в переменную q. Здесь использовано то

тора цикла сумма вычислена с учетом слагаемого для значения индексной переменной со значением n-1, а переменная q имеет значение добавки для следующего итерационного шага. Этот шаг реализуется уже после оператора цикла командой y=z+q, в результате чего переменная y получает нужное значение. На рис. 3.25 показано окно редактора m-файлов с кодом функции

MyExp().

Рис. 3.25. Программный код функции с оператором цикла для вычисления экспоненты

Результат вычисления экспоненты для единичного первого аргумента (аргумент в экспоненциальной зависимости) и различных значений второго аргумента (верхний индекс суммы ряда) представлен на рис. 3.26.

Стоит отметить, что чем больше по абсолютной величине первый аргумент, тем больше необходимо учитывать слагаемых при расчете экспоненты.

Синтаксис вызова оператора while такой:

while условие команды

end

127

Самоучитель Matlab

Рис. 3.26. Результат вычисления экспоненты по разному числу слагаемых в ряде

После ключевого условия while указывается условие. Это условие проверяется, и если оно истинно, выполняются команды, указанные после этого условия, вплоть до инструкции окончания оператора end. Затем снова проверяется условие. Работа оператора while завершается, если условие становится ложным. Отсюда следует, что команды в операторе while должны быть такими, чтобы их выполнение на каком-то этапе приводило к изменению значения условия, иначе цикл будет бесконечным. Хотя это

инеобязательно: работа условных операторов и операторов цикла может быть прервана с помощью инструкции break. Существует инструкция

идля досрочного завершения работы функции – это инструкция return. На рис. 3.27 показано окно редактора m-файлов с кодом функции, в которой использован оператор цикла while.

Рис. 3.27. Окно редактора m-файлов с кодом функции, в которой использован оператор while

Код функции SqrAvr() приведен ниже:

128

Глава 3. Элементы программирования

function s=SqrAvr(n) sum=0;

i=1; while i<=n

sum=sum+i*i;

i=i+1;

end s=sum/n; end

в качестве результата. Сразу оговоримся, что имеет место соотношение

ректности работы функции. Результат вызова функции приведен в документе на рис. 3.28.

Рис. 3.28. Результат вызова функции SqrAvr()

Легко видеть, что значение вычислено корректно. Что касается самого программного кода, использованного для вычислений, то он достаточно прост. Вначале объявляются локальные переменные sum (используется для вычисления суммы квадратов натуральных чисел, начальное значение равно 0) и i (индексная переменная с начальным значением 1). В операторе цикла while проверяется условие i<=n (индексная переменная не превышает значение аргумента n функции SqrAvr()). В теле оператора цикла выполняется команда sum=sum+i*i, которой на величину квадрата индексной переменной i увеличивается значение переменной sum, а затем командой i=i+1 на единицу увеличивается значение индексной переменной. После завершения работы оператора цикла командой s=sum/n в переменную s записывается значение функции SqrAvr().

129

Самоучитель Matlab

Логические значения и логические операторы

Все выглядит очень логично, Штирлиц.

К/ф "Семнадцать мгновений весны"

Как уже упоминалось в первой главе книги, в Matlab в качестве логического значения истина используется единица, а в качестве логического значения ложь используется ноль. Другими словами, любое логическое выражение, если оно истинно, интерпретируется как единица, а если ложно – как ноль. Более того, если числовое значение употребляется в качестве логического выражения, то ненулевое значение интерпретируется как истина, а нулевое значение интерпретируется как ложь.

Особый интерес представляют возможные операции, которые применимы к логическим значениям, а также способы получения и обработки логических массивов. Начнем с логических операций, логических функций и логических операторов. Сюда же отнесем и операторы сравнения, которые часто используются в логических выражениях.

На заметку

В первой главе мы кратко познакомились с логическими и условными операторами. Здесь мы несколько расширим свои познания в этой области.

Некоторые операторы сравнения уже использовались нами ранее. Для удобства список операторов сравнения приведен в табл. 3.1 вместе с встроенными функциями, используемыми для сравнения значений.

Табл. 3.1. Операторы сравнения

130