1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 4. Элементы матричной алгебры

данова форма), которая получается в результате преобразования исходной матрицы. Пример вычислений приведен ниже (жирным шрифтом выделен ввод пользователя):

>> A=[5 -3 2;6 -4 4;4 -4 5]

A =

>> inv(U)*A*U ans =

1.0000 -0.0000 -0.0000 -0.0000 2.0000 0.0000 0.0000 -0.0000 3.0000

>> U*B*inv(U) ans =

5.0000 -3.0000 2.0000

6.0000 -4.0000 4.0000

4.0000 -4.0000 5.0000

191

Самоучитель Matlab

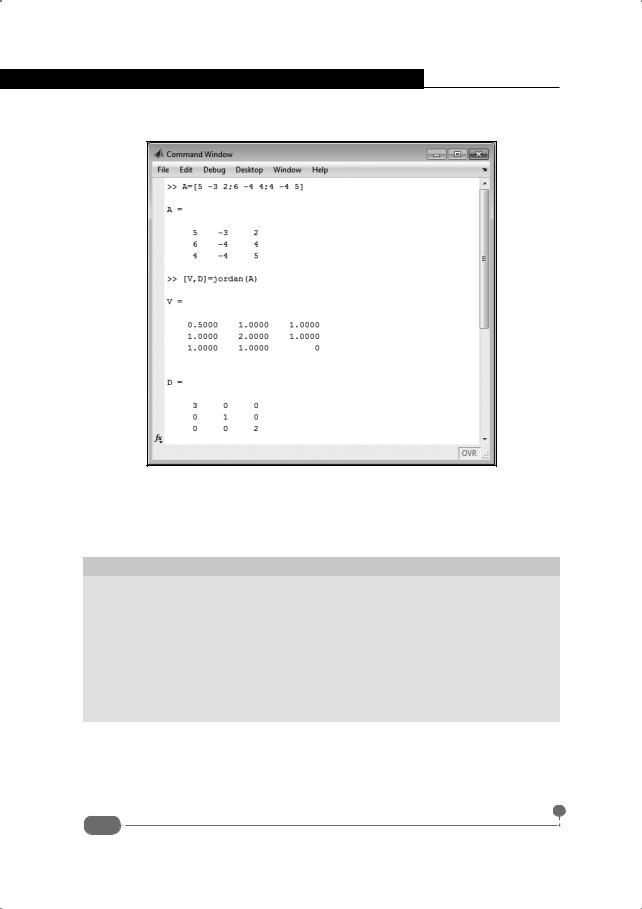
На рис. 4.31 представлена начальная часть документа с командным кодом, в котором матрица диагонализируется с помощью функции jordan().

Рис. 4.31. Диагонализация матрицы с помощью функции jordan()

После объявления матрицы A командой [V,D]=jordan(A) вычисляется матрица преобразования V и диагональная (в данном случае) матрица D – результат преобразования матрицы A.

На заметку

По определению функцией jordan() на основании матрицы ˆ (аргумент

A

нальная или, в общем случае, имеет жорданов вид (блочно-диагональная). Из

в общем случае не выполняется. Поэтому не совсем корректно называть матри-

цу ˆ матрицей перехода в том смысле, как это излагалось выше. Для устране-

V

ния возможных недоразумений будем называть матрицу ˆ матрицей преобра-

V

зования.

этого используем команды inv(V)*A*V и V*D*inv(V) соответственно. В первом случае получаем матрицу D, а во втором случае получаем матрицу A (рис. 4.32).

192

Глава 4. Элементы матричной алгебры

Рис. 4.32. Проверка результата диагонализации

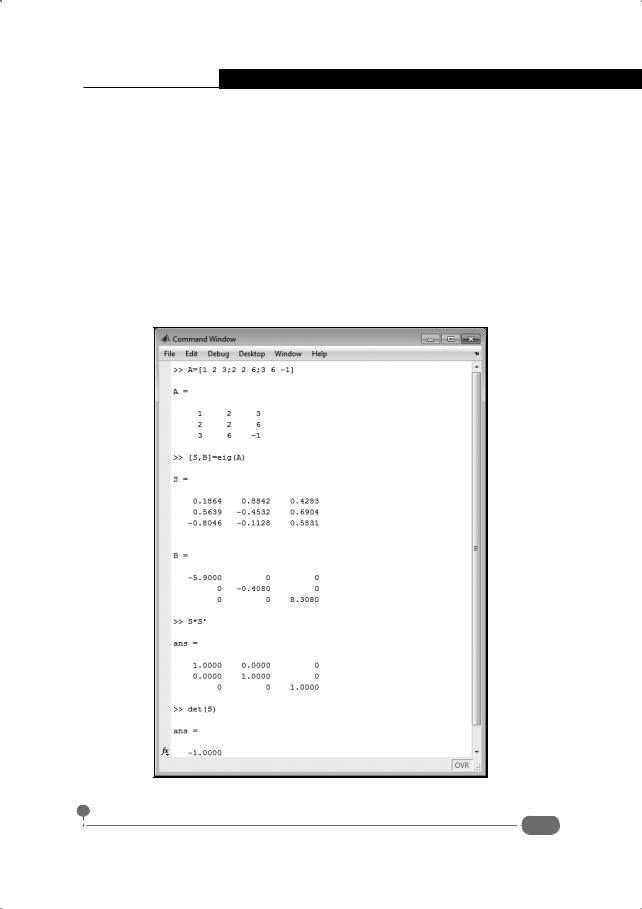
Практически те же результаты можно получить с помощью функции eig(). На рис. 4.33 приведен фрагмент документа, в котором командой [U,B]=eig(A) на основе матрицы A вычисляется диагональная матрица B и матрица преобразования U.

В результате выполнения команды inv(U)*A*U получаем матрицу B, а в результате выполнения команды U*B*inv(U) получаем матрицу A. При этом матрица B фактически совпадает с матрицей D, вычисленной ранее, – те же собственные числа на диагонали, только в другом порядке. Возникает естественный вопрос: в чем же разница? Разница есть, и она существенная. Связана она в основном с матрицей преобразования. Столбцы матрицы преобразования, возвращаемой функцией eig(), нормированы на единицу, чего не скажешь о матрице преобразования, возвращаемой функцией jordan().

На заметку

Порядок следования собственных чисел на диагонали у диагональной матрицы определяет порядок следования столбцов в матрице перехода. Другими словами, при диагонализации матрицы конечная диагональная форма содержит на главной диагонали собственные числа исходной матрицы. В принципе, они могут следовать в разном порядке. Матрицы перехода для разных диагональных форм отличаются порядком следования столбиков. Сами столбики матрицы преобразования представляют собой собственные векторы исходной матрицы.

Имеет смысл также рассмотреть процедуру диагонализации симметричной матрицы. Матрицу создаем так:

193

Самоучитель Matlab

Рис. 4.33. Диагонализация матрицы с помощью функции eig()

>> A=[1 2 3;2 2 6;3 6 -1]

A =

1 2 3

2 2 6

36 -1

Матрицу перехода и диагональную форму вычисляем следующей командой:

194

Глава 4. Элементы матричной алгебры

В данном случае получена именно матрица перехода, поскольку произведение этой матрицы на транспонированную дает единичную матрицу:

Ее определитель по модулю равен единице:

>> det(S) ans =

-1.0000

Процесс этих вычислений проиллюстрирован на рис. 4.34.

Рис. 4.34. Диагонализация симметричной матрицы с помощью функции eig()

195

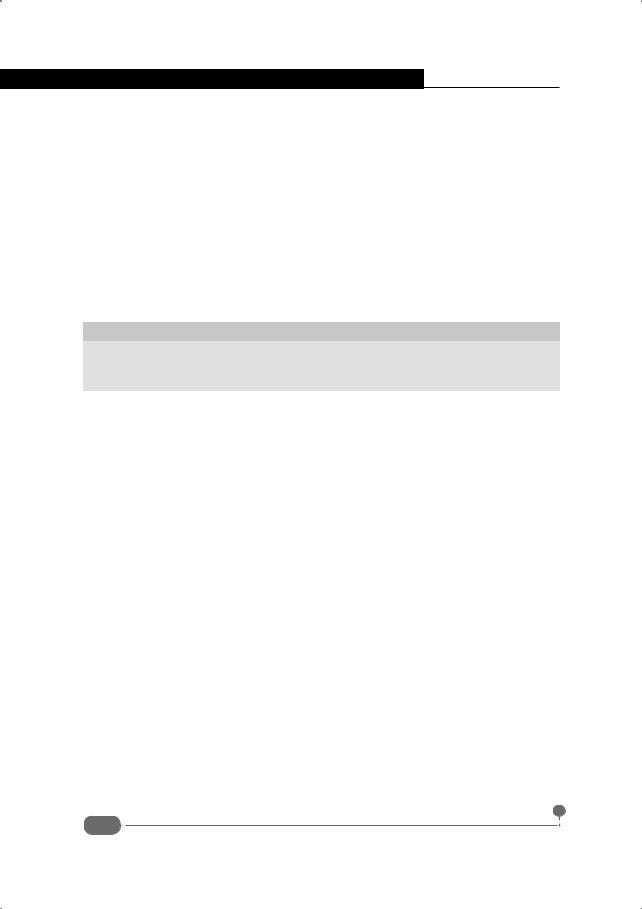
Самоучитель Matlab

В принципе, похожие результаты можно получить и с помощью функции jordan(). Правда, процесс более сложный. Например, следующей командой вычисляем матрицу преобразования и соответствующую ей диагональную форму:

На заметку

Формально элементы полученных матриц комплексные. Однако мнимая часть у них нулевая. Появление нулевых мнимых частей связано со спецификой используемого алгоритма вычисления жордановой формы и матрицы перехода.

Однако транспонированная матрица преобразования не равна обратной, в чем несложно убедиться, воспользовавшись командой

Результаты этих вычислений представлены на рис. 4.35.

Причина этой неприятности кроется в том, что хотя столбцы полученной матрицы преобразования состоят из собственных векторов исходной, преобразуемой, матрицы, они не нормированы. В этом все дело! Убедимся.

Переопределяем матрицу преобразования путем нормирования столбца матрицы на модуль этого столбца. Чтобы нормировать столбец с индексом k (возможные значения 1, 2 или 3), используем команду W(:,k)/ norm(W(:,k)). Здесь мы воспользовались тем, что ссылка на столбец матрицы с данным индексом выполняется в виде W(:,k). Вся команда переопределения матрицы W выглядит так:

>> W=[W(:,1)/norm(W(:,1)),W(:,2)/norm(W(:,2)),W(:,3)/ norm(W(:,3))]

196

Глава 4. Элементы матричной алгебры

Рис. 4.35. Диагонализация симметричной матрицы с помощью функции jordan()

Теперь все изменилось, и произведение матрицы W на транспонированную дает единичную матрицу:

При этом матрица W является матрицей перехода:

Ее определитель равен единице:

>> det(W) ans =

1.0000 - 0.0000i

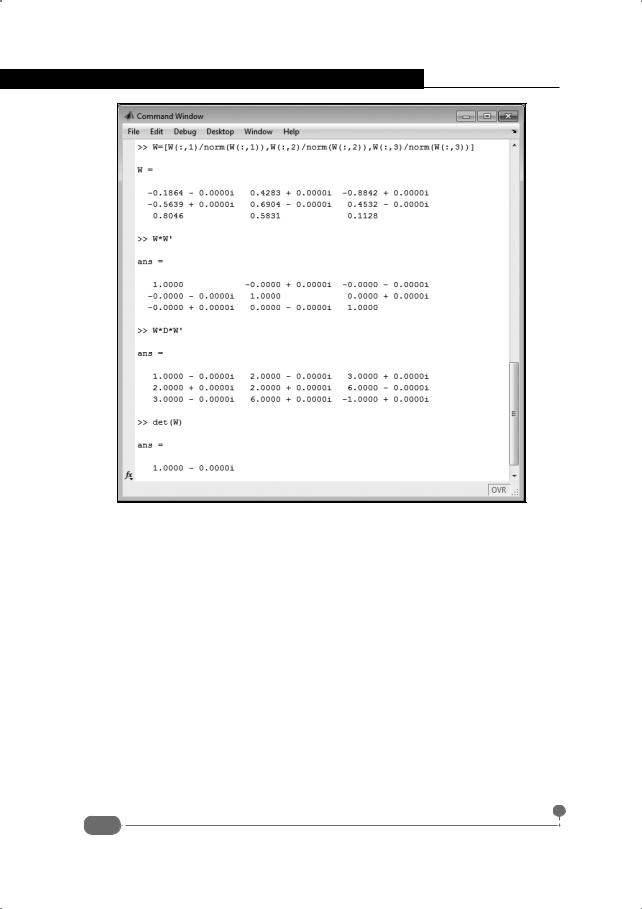
Результаты этих вычислений представлены на рис. 4.36.

197

Самоучитель Matlab

Рис. 4.36. Создание на основе матрицы преобразования матрицы перехода

В заключение отметим, что если необходимо только вычислить конечную диагональную форму, без вычисления матрицы перехода, можно воспользоваться функцией diag(), которой создается диагональная матрица. Аргументом функции передается вектор (список) диагональных значений. Так, если нужно создать диагональную форму для матрицы A, можно воспользоваться командой diag(eig(A)).

198

Глава 5 Решение уравнений и оптимизация

- Для себя я все решил. - Здесь решаю я!

К/ф "Клуб самоубийц, или Приключения титулованной особы"

В этой главе обсуждаются методы решения средствами Matlab алгебраических уравнений и систем уравнений, а также задачи оптимизации и математического (линейного и нелинейного) программирования. Сначала рассмотрим методы решения нелинейных алгебраических уравнений. Напомним, что системы линейных уравнений рассматривались в предыдущей главе в качестве примера операций с матрицами и векторами, поэтому здесь на них останавливаться не будем.

Наше изучение методов решения уравнений начнем с краткого миниобзора встроенных функций Matlab, предназначенных для этого. Затем остановимся на некоторых методах реализации поиска корней уравнений и систем уравнений средствами программирования.

Встроенные функции для решения уравнений

Курс у нас один – правильный.

В. Черномырдин

Для решения одного, отдельного уравнения можно воспользоваться встроенной функцией fzero(). У функции несколько способов вызова. Мы рассмотрим те, что наиболее востребованы с практической точки зрения. Допустим, нам необходимо решить уравнение f (x) = 0 . Функция f (x) полностью определяет решаемое уравнение. Ссылку на эту функцию необходимо передать первым аргументом функции fzero(). Ссылкой может служить указатель на функцию, имя (без расширения и в одинарных кавычках) m-файла с кодом функции или заключенное в одинарные кавычки выражение, определяющее функциональную зависимость f (x). В последнем случае независимая переменная должна называться x , и никак иначе.

Обычно для поиска решения в числовом виде (а именно об этом идет речь) указывают интервал, на котором ищется решение или, по крайней мере, начальное приближение для корня. Начальное приближение или интервал поиска (в виде списка из двух элементов – границ интервала) передается вторым аргументом функции fzero().

199

Самоучитель Matlab

На заметку

Если вторым аргументом передается интервал поиска корня, то на границах интервала функция уравнения должна принимать значения разных знаков, иначе функцией fzero() результат вычислен не будет.

Возвращает функция fzero() много полезной информации. Но самое главное – она возвращает корень уравнения. Рассмотрим пример, представленный в документе на рис. 5.1.

Рис. 5.1. Решение уравнения с помощью функции fzero() на интервале

Командой x=fzero('2*sin(x)^2+sin(x)-1',[0 pi/2]) вычисляется корень уравнения 2 sin(x)2 + sin(x) −1 = 0 на интервале значений переменной x от 0 до π 2 (на этом интервале точное решение x = π 6 ). Если воспользоваться командой x=fzero('2*sin(x)^2+sin(x)-1', [pi/2 pi]), получим решение этого же уравнения на интервале от π 2 до π (решение x = 5π6 ).

На рис. 5.2 приведен фрагмент документа, в котором вместо интервала поиска решения указывается начальная точка для поиска решения.

Рис. 5.2. При вычислении корня указывается начальное значение для поиска решения

200