
1-2 Моделирование / Matlab. Практический подход. Самоучитель
.pdf
Глава 1. Принципы работы Matlab и основы вычислений
состоящая их строк с i-й по j-ю и одновременно столбцов с m-го по n-й. Рассмотрим некоторые примеры использования оператора "двоеточие". В частности, исходная матрица A вводится командой
A=[1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16]
A = |
2 |
3 |
4 |
1 |
|||
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Как и ранее, здесь и далее жирным шрифтом выделен ввод пользователя. В следующих командах оператор "двоеточие" используется для извлечения подматриц из исходной матрицы A:
>>A(1:3,2) ans =
2
6
10
>>A(3,2:4) ans =
10 11 12 >> A(3:4,1:2) ans =
9 10
13 14
Например, командой A(1:3,2) возвращается вектор-столбец, составленный из элементов с первой по третью строку во втором столбце матрицы A. Командой A(3,2:4) возвращается вектор-строка, который составлен из элементов третьей строки со второго по четвертый столбец включительно матрицы A. Наконец, командой A(3:4,1:2) возвращается подматрица матрицы A, верхний левый элемент которой имеет индексы (3,1), а правый нижний элемент имеет индексы (4,2).
Встроенные математические функции
Ну зачем такие сложности?
К/ф "Приключения Шерлока Холмса и доктора Ватсона. Собака Баскервилей"
В Matlab по умолчанию доступно достаточно большое количество встроенных функций. Ядро их составляют математические функции, которые на практике используются сравнительно часто. Некоторые из них перечислены в табл. 1.5.
31

Самоучитель Matlab
Табл. 1.5. Некоторые математические функции Matlab
Функция |
Описание |
|
|
abs() |
Модуль числа (в том числе и комплексного), указанного аргумен- |
том функции |
|
|
|
acos() |
Арккосинус для числа, указанного аргументом функции |
acosd() |
Арккосинус аргумента функции. Результат представлен в граду- |
сах |
|
|
|
acot() |
Арккотангенс числа, указанного аргументом функции |
acotd() |
Арккотангенс аргумента функции. Результат представлен в гра- |
дусах |
|
|
|
acsc() |
Арккосеканс числа, указанного аргументом функции |
acscd() |
Арккосеканс аргумента функции. Результат представлен в гра- |
дусах |
|
|
|
asec() |
Арксеканс числа, указанного аргументом функции |
asecd() |
Арксеканс аргумента функции. Результат представлен в градусах |
asech() |
Арксеканс гиперболический от числа, указанного аргументом |
функции |
|
|
|
asin() |
Арксинус от числа, указанного аргументом функции |
asind() |
Арксинус аргумента функции. Результат представлен в градусах |
asinh() |
Арксинус гиперболический от числа, указанного аргументом |
функции |
|
|
|
atan() |
Арктангенс от числа, переданного аргументом функции |
|
У функции два аргумента (например, atan(y,x)). В качестве |
atan2() |
результата возвращается направление (угол в диапазоне зна- |
чений от -π до π) на точку с соответствующими координатами |
|
|
(в данном случае, точка с координатами (y,x)). Если аргументы |
|
комплексные, их мнимые части игнорируются |
atand() |
Арктангенс аргумента функции. Результат представлен в градусах |
atanh() |
Арктангенс гиперболический от числа, переданного аргументом |
функции |
|
|
|
ceil() |
Функция округления аргумента в направлении плюс бесконеч- |
ности – округление выполняется до целого значения, которое не |
|
|
меньше, чем аргумент |
|
|
cos() |
Косинус от числа, переданного аргументом функции |
cosd() |
Косинус аргумента функции, указанного в градусах |
cosh() |
Косинус гиперболический от числа, переданного аргументом |
функции |
|
|
|
cot() |
Котангенс от числа, переданного аргументом функции |
cotd() |
Котангенс аргумента функции, указанного в градусах |
coth() |
Котангенс гиперболический от числа, переданного аргументом |
функции |
|
|
|
csc() |
Косеканс от числа, переданного аргументом функции |
32

|
|
Глава 1. Принципы работы Matlab и основы вычислений |
|||
|
|
|
|
|
|
Функция |
|
Описание |
|
||
|
|
|
|
|
|
cscd() |
Косеканс аргумента функции, указанного в градусах |
|
|||
csch() |
Косеканс гиперболический от числа, переданного аргументом |
|
|||
функции |
|
|
|
||
|
|
|
|
|
|
exp() |
Экспонента: показательная функция с основанием-константой Эй- |
|
|||
лера и показателем степени, определяемым аргументом функции |
|
||||
|
|
|
|
|
|
expm1() |
Командой вида expm1(x) с повышенной точностью вычисляет- |
||||
ся значение |
|
|
|
||
|
|
exp(x)-1 |
|
|
|
factor() |
Функцией возвращается вектор-строка с простыми множителями |
|
|||
числа (с учетом их кратности), указанного аргументом функции |
|
||||
|
|
|
|
|
|
factorial() |
Функция для вычисления факториала числа, указанного аргумен- |
|
|||
том функции |
|
|
|
||
|
|
|
|
|
|
fix() |
Функция округления в направлении нуля. Результатом является |
|
|||
число, получающееся округлением аргумента функции до бли- |
|
||||
|
жайшего целого значения в направлении нуля |
|
|||
|
|
|
|
|
|
floor() |
Функция округления аргумента до ближайшего целого значения, |
|
|||
которое не превышает аргумент, – округление в направлении ми- |
|
||||
|
нус бесконечности |
|
|
|
|
|
|
|
|
|
|
gcd() |
Функцией возвращается наибольший общий делитель целых чи- |
|
|||
сел или целочисленных массивов – аргументов функции |
|
||||
|
|
|
|
|
|
hypot() |
Корень квадратный из суммы квадратов модулей аргументов, |
|
|||
переданных функции |
|
|
|
||
|
|
|
|
|
|
|
У функции два аргумента. Результатом является целая часть от |
|
|||
idivide() |
деления первого аргумента на второй. Можно также указать оп- |
|
|||
цию – в одинарных скобках имя функции, с помощью которой вы- |
|
||||
|
полняется округление |
|
|
|
|
|
|
|
|
|
|
lcm() |
Функцией в качестве результата возвращается наименьшее об- |
|
|||
щее кратное для целых чисел или целочисленных массивов – ар- |
|
||||
|
гументов функции |
|
|
|
|
|
|
|
|
|
|
log() |
Натуральный логарифм от числа, указанного аргументом функции |
|
|||
log10() |
Логарифм по основанию 10 от числа, указанного аргументом |
|
|||
функции |
|
|
|
||
log1p() |
Командой вида log1p(x) с повышенной точностью вычисляет- |
|
|||
ся значение |
|
|
|
||
|
|
log(1+x) |
|
|
|
log2() |
Логарифм по основанию 2 от числа, указанного аргументом |
|
|||
функции |
|
|
|
||
mod() |
Функцией возвращается остаток от деления значения первого ар- |
|
|||
гумента функции на значение второго аргумента. Целая часть от |
|
||||
|
деления определяется функцией froor() |
|
|||
|
Функциейвкачествезначениявозвращаютсябиномиальныекоэф- |
|
|||
|
фициенты. Если функция вызвана в формате nchoosek(n,k), |
|
|||
nchoosek() |
то в качестве результата возвращается значение |
|
|||
|
Cnk = |
n ! |
|
|
|
|
|
k !(n −k)! |
|
||
|
|
|
|
||
|
|
|
|
|
|
33

Самоучитель Matlab
Функция |
Описание |
|
|
nextpow2() |
Функцией в качестве значения возвращается ближайшее целое |
число – степень двойки, которое не меньше модуля аргумента |
|
|
функции |
|
|
nthroot() |
Командой nthroot(x,n) в качестве значения возвращается |
корень порядка n (второй аргумент) из действительного числа |
|
|
или элементов действительного массива x (первый аргумент ) |
|
Функция может вызываться с одним или двумя аргументами. Если |
|
у функции один аргумент (массив) и функция вызывается в фор- |
pow2() |
мате pow2(x), то в качестве результата возвращается массив |
степеней двойки, показатели степени определяются массивом |
|
|
x. Если функция вызывается с двумя аргументами в формате |
|
pow2(x,y), то результатом является x.*2.^y |
|
У функции два аргумента. Если аргументы скалярные, в каче- |
power() |
стве результата возвращается значение первого аргумента, воз- |
веденное в степень, определяемую вторым аргументом. В бо- |
|
|
лее общем случае в качестве результата выполнения команды |
|
power(A,B) возвращается 'A.^B' |
primes() |
Функцией генерируется список простых чисел. Количество чисел |
указывается аргументом функции |
|
|
|
rem() |
Функцией возвращается остаток от деления значения первого ар- |
гумента функции на значение второго аргумента. Целая часть от |
|
|
деления определяется функцией fix() |
round() |
Функция округления аргумента до ближайшего целого значения |
sec() |
Секанс от числа, указанного аргументом функции |
secd() |
Секанс аргумента функции, указанного в градусах |
sign() |
Знак числа, указанного аргументом функции (для положительных |
чисел – единица, для отрицательных чисел – минус единица, для |
|
|
нуля - ноль) |
|
|
sin() |
Синус от числа, указанного аргументом функции |
sind() |
Синус аргумента функции, указанного в градусах |
sqrt() |
Корень квадратный из числа, указанного аргументом функции |
tan() |
Тангенс от числа, указанного аргументом функции |
tand() |
Тангенс аргумента функции, указанного в градусах |
Хотя большинство из представленных выше функций с математической точки зрения определены для скалярных величин, обычно они могут применяться и для аргументов-матриц. В этом случае действие функционального оператора применяется к каждому из элементов матрицы. Например, если переменная A является матрицей с элементами A(i,j), то в результате выполнения команды exp(A) получим матрицу того же ранга, а ее элементы вычисляются как exp(A(i,j)). В некоторых случаях такой подход неприемлем. Существуют так называемые матричные функции, аргументами которых по определению являются матрицы (в основном квадратные). Результат этих функций вычисляется по алгоритмам, разработанным специ-
34
Глава 1. Принципы работы Matlab и основы вычислений
ально для матриц. Так, в Matlab есть встроенные матричные функции для экспоненты, логарифма и квадратного корня. Это соответственно функции expm(), logm() и sqrtm(). Например, если A – квадратная матрица, то функцией expm(A) вычисляется матричная экспонента. По определению
∞ An
это ряд exp(A) = ∑ . Результатом является матрица, которая вычис-
n=0 n !
ляется, как правило, на основе собственных чисел и собственных векторов матрицы A. Матричный логарифм для аргумента-матрицы A, вычисляемый инструкцией logm(A), представляет собой матрицу такую, что матричная экспонента от нее равна матрице A. Другими словами, по определению если B=logm(A), то expm(B)=A, и функция logm() является обратной к функции expm(). Аналогично, в результате извлечения квадратного корня из матрицы A с помощью функции sqrtm() получаем матрицу, которая, будучи возведенной в квадрат, дает матрицу A. Например, если B=sqrtm(A), то B*B=A.
В Matlab также широко представлены специальные функции, некоторые их них приведены в табл. 1.6.
Табл. 1.6. Некоторые специальные математические функции Matlab
Функция |
|
|
|
|
|
|
|
Описание |
|
|
|
|
|
||||
|
Функция Эйри. Командой airy(x) в качестве результата |
||||||||||||||||
|
возвращается функция y(x), являющаяся одним из реше- |
||||||||||||||||
|
ний уравнения |
d2y(x) |
−xy(x) = 0, а именно возвращается |
||||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
dx2 |
|
x |
K1 3 ( |
2 |
x3 2 ), где |
|||||||
|
функция Эйри первого рода Ai(x) = |
1 |
|
||||||||||||||
|
π |
3 |
3 |
||||||||||||||
|
Kν (z) - модифицированная функция Бесселя второго рода |
||||||||||||||||
airy() |
индекса ν |
. Функция также может вызываться с двумя аргу- |
|||||||||||||||
ментами в формате airy(k,x). В этом случае для k=0 |
|||||||||||||||||
|
|||||||||||||||||
|
возвращается функция Ai(x), для k=1 возвращается произ- |
||||||||||||||||
|
водная Ai′(x), для k=2 возвращается независимое решение |
||||||||||||||||
|
Bi(x) = |
|
x |
(I−1 3 ( |
2 |
x3 2 )+ I1 3 ( |
2 |
x3 2 )), где Iν (z) - моди- |
|||||||||
|
|
3 |
3 |
3 |
|||||||||||||
|
фицированная функция Бесселя первого рода индекса ν , для |
||||||||||||||||
k=3 возвращается производная Bi′(x)
|
Функция Бесселя третьего рода |
(функция |
Ханкеля). |
||
|
При |
вызове функции с |
тремя аргументами |
в форма- |
|
besselh() |
те |
besselh(n,k,x) |
возвращается функция Ханкеля |
||
Hn(k)(x) = Jn(x) +(−1)k +1iYn(x), где |
k = 1,2 , |
а Jn(x) и |
|||
|
Yn(x) - функции Бесселя индекса n первого и второго рода со- |
||||
|
ответственно |
|
|
|
|
35

Самоучитель Matlab
Функция |
|
|
|
|
|
|
|
Описание |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Командой besseli(n,x) возвращается модифи- |
||||||||||||||||||||||||||
|
цированная |
функция |
Бесселя |
первого |
|
рода |
(индекса n) |
||||||||||||||||||||
|
|
|
x |
n |
∞ |
(x 2)2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
besseli() |
In(x) = ( |
|
) |
∑ |
|
|
|
(где |
Γ(z) |
- гамма-функция |
|||||||||||||||||
2 |
k ! Γ(n + k +1) |
||||||||||||||||||||||||||
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Эйлера), которая является одним из решений модифицированно- |
||||||||||||||||||||||||||
|
го уравнения Бесселя x2y′′(x) + xy′(x) −(x2 + n2)y(x) = 0 |
||||||||||||||||||||||||||
|
Командой besselj(n,x) возвращается функция Бесселя |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
∞ |
|
k |
2k |
||||||
|
первого рода (индекса n) Jn(x) = ( |
)n |
∑ |
|
(−1) (x 2) |
||||||||||||||||||||||
besselj() |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
k =0 k ! Γ(n + k +1) |
||||||||||||
|
(где Γ(z) - гамма-функция Эйлера), которая является одним из |
||||||||||||||||||||||||||
|
решений уравнения Бесселя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x2y′′(x) + xy′(x) +(x2 −n2)y(x) = 0 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Командой besselk(n,x) возвращается модифи- |
||||||||||||||||||||||||||
|
цированная |
функция |
Бесселя |
второго |
|
рода |
(индекса n) |
||||||||||||||||||||
|
Kn(x) = |
π I−n(x) −In(x) |
(где |
|
|
In(x) - |
модифицирован- |
||||||||||||||||||||
besselk() |
2 |
|
|
sin(πn) |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ная функция Бесселя первого рода), которая является од- |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
ним |
из решений модифицированного |
|
уравнения Бесселя |
|||||||||||||||||||||||
|
x2y′′(x) + xy′(x) −(x2 + n2)y(x) = 0 . Для |
целых |
индексов |
||||||||||||||||||||||||
|
соответствующее выражение рассчитывается как лимит |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Командой besselj(n,x) возвращается функция Бесселя |
||||||||||||||||||||||||||
|
второго рода (индекса n) Yn(x) = |
J−n(x)cos(πn) −Jn(x) |
|||||||||||||||||||||||||
bessely() |
|
|
|
|
|
|
sin(πn) |
|
|||||||||||||||||||
(где Jn(x) |
- функция |
Бесселя первого |
рода), кото- |
||||||||||||||||||||||||
|
рая |
является |
одним из |
решений |
|
уравнения |
Бесселя |
||||||||||||||||||||
|
x2y′′(x) + xy′(x) +(x2 −n2)y(x) = 0 . Для |
целых |
индексов |
||||||||||||||||||||||||
|
соответствующее выражение рассчитывается как лимит |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
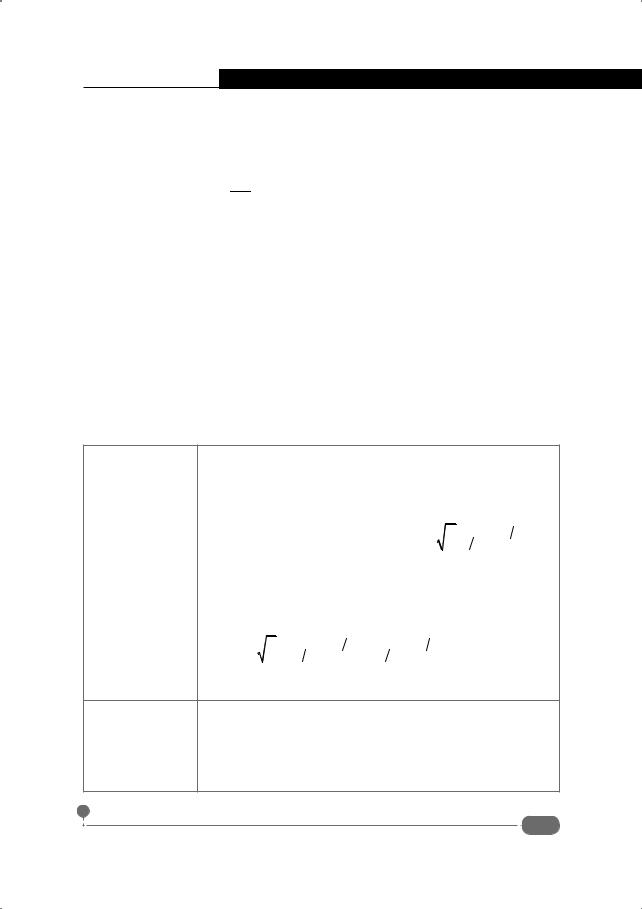
|
Бета-функция Эйлера. Командой beta(x,y) возвращается |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Γ(x)Γ(y) |
||||
beta() |
значение функции B(x,y) = ∫tx −1(1 −t)y−1dt = |
||||||||||||||||||||||||||
|
, |
||||||||||||||||||||||||||
Γ(x + y) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Γ(x) - гамма-функция Эйлера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Неполная бета-функция Эйлера. Командой betainc(z,x,y) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
z |
|
|
|
|
|
|
|||||||
betainc() |
возвращается значение Iz (x,y) = |
∫tx −1(1 −t)y−1dt , |
|||||||||||||||||||||||||
B(x,y) |
|||||||||||||||||||||||||||
|
где B(x,y) - бета-функция Эйлера |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
betaln() |
Логарифм натуральный от бета-функции Эйлера. Аргументами |
||||||||||||||||||||||||||
передаются аргументы бета-функции |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36

|
|
|
Глава 1. Принципы работы Matlab и основы вычислений |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Функция |
|
|
|
|
|
|
|
Описание |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Эллиптическая функция Якоби. Если функция вызывается с дву- |
|
|||||||||||||||||||
|
мя аргументами в формате ellipj(u,m), в качестве резуль- |
|
|||||||||||||||||||
|
тата возвращаются значения (вектор) для функций sn(u), cn(u) |
|
|||||||||||||||||||
ellipj() |
и dn(u), которые вычисляются на основе эллиптического инте- |
|
|||||||||||||||||||
|
|
ϕ |
dθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
грала u = ∫ |
|
|
|
|
|
и определяются из соотношений |
|
|||||||||||||
|
|
|
2 |
|
|
|
|
||||||||||||||
|
0 |
|
1 −m sin |
(θ) |
|
|
1 −m sin2(ϕ) |
|
|||||||||||||
|
sn(u) = sin(ϕ) , cn(u) |
= cos(ϕ) и dn(u) = |
|
|
|||||||||||||||||
|
Функция для вычисления полного эллиптического интеграла пер- |
|
|||||||||||||||||||
|
вого и второго рода (вектор значений). Эллиптический интеграл |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π 2 |
|
|
|
|
||
|
первого рода |
вычисляется |
|
как K(m) = ∫ |
|
dθ |
|
|
. |
|
|||||||||||
ellipke() |
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 −m sin |
(θ) |
|
|||
|
Эллиптический интеграл |
|
второго |
рода |
вычисляется |
|
как |
|
|||||||||||||
|
|
π 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
E(m) = ∫ |
1 −m sin2(θ)dθ |
|
|
|
|
|
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Функция ошибок. Командой erf(x) возвращается значение |
|
|||||||||||||||||||
erf() |
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
erf (x) = |
∫ exp(−t2)dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция ошибок (остаточная). Командой erfc(x) возвраща- |
|
|||||||||||||||||||
erfc() |
|
|
|
|
|
|
|
2 |
+∞ |
|
|
|
|
|
|
|
|||||
ется значение erfc(x) = |
∫ exp(−t2)dt = 1 −erf (x) |
|
|
|
|||||||||||||||||
π |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||
erfcx() |
Функция ошибок (остаточная нормированная). Командой |
|
|||||||||||||||||||
erfcx(x)возвращается значение erfcx(x) = exp(x2)erfc(x) |
|
||||||||||||||||||||
erfinv() |
Обратная функция к функции ошибок erf(). Если y=erf(x), |
|
|||||||||||||||||||
то erfinv(y)=x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
erfcinv() |
Обратная функция к |
|
функции |
ошибок |
|
erfc(). |
Если |
|
|||||||||||||
y=erfc(x), то erfcinv(y)=x |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
Интегральная экспонента. Командой expint(x) возвращает- |
|
|||||||||||||||||||
expint() |
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ся значение E1(x) = |
∫ |
|
exp(−t) |
dt |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гамма-функция Эйлера. Командой gamma(x) возвращается |
|
|||||||||||||||||||
gamma() |
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значение Γ(x) = ∫tx −1 exp(−t)dt |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Неполная гамма-функция. Командой gammainc(z,x) воз- |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
z |
|
|
|
|
|
|
|
gammainc() |
вращается значение P(z,x) = |
∫tx −1 exp(−t)dt , Γ(x) - |
|
||||||||||||||||||
Γ(x) |
|
||||||||||||||||||||
|
гамма-функция |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37

Самоучитель Matlab
Функция |
|
|
|
|
Описание |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||||
gammaln() |
Логарифм натуральный от гамма-функции Эйлера. Аргументом |
||||||||||||||
функции передается аргумент гамма-функции |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||
|
Функция для вычисления присоединенных полиномов Лежан- |
||||||||||||||
|
дра. Присоединенные полиномы Лежандра определяются как |
||||||||||||||
|
|
m |
|
m |
2 m 2 |
dm |
|
|
|
|
|
|
|
|
|
|
P |
|
(x) = (−1) (1 −x |
) |
|
P (x) (присоединенный поли- |
|||||||||
|
|
dxm |
|||||||||||||
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
||
legendre() |
ном Лежандра степени n порядка m ), где полиномы Лежандра |
||||||||||||||
|
|
|
|
|
|
n |
|
|
|
1 |
|
dn |
|
||
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|||
|
степени |
n определяются как P |
(x) = |
|
|
|
|
|
|
(x2 −1)n . |
|||||
|
2 |
n ! |
|
||||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|||||
|
В результате вызова функции в формате legendre(n,x) |
||||||||||||||
|
возвращается вектор-столбец значений присоединенных поли- |
||||||||||||||
|
номов Лежандра Pm(x) для m = 0,1,2,...,n |
|
|
|
|||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Пси-полигамная функция. Если функция вызывается с одним |
||||||||||||||
|
аргументом в формате psi(x), в качестве результата воз- |
||||||||||||||
|
вращается логарифмическая производная от гамма-функции |
||||||||||||||
psi() |
ψ(x) = |
Γ′(x) (пси-функция). Если функция вызывается с дву- |
|||||||||||||
|
|
|
|
Γ(x) |
|
|
|
|
|
|
|
|
|
|
|
|
мя аргументами в формате psi(k,x), в качестве результата |
||||||||||||||
|
возвращается k-я производная от пси-функции, то есть ψ(k)(x) |
||||||||||||||
Как и в случае с базовыми математическими функциями, для большинства специальных функций аргументами могут указываться матрицы. В этом случае функция вычисляется для каждого из элементов матрицы.
На заметку
Описанные в этом разделе функции составляют малую толику всех встроенных функций Matlab. Многие из них рассматриваются далее в книге в контексте освещаемых вопросов.
Формат вывода числовых данных
Если сразу не разберешь, Плох он или хорош...
В. Высоцкий, "Песня о друге"
В некоторых случаях приходится изменять способ, которым данные с результатом выполнения команд пользователя выводятся на экран. В первую очередь отметим, что можно вообще не отображать результат выполнения команды в командном окне. Для этого достаточно соответствующую команду закончить точкой с запятой (то есть ;). В этом случае после нажатия клавиши <Enter> команда выполняется, но результат ее выполнения в командном окне не отображается. Такой режим особенно удобен в тех случаях, когда нужно выполнять громоздкие промежуточные расчеты, ко-
38

Глава 1. Принципы работы Matlab и основы вычислений
торые, с одной стороны, необходимы для получения конечного результата, а с другой – загромождают рабочее пространство. Поэтому разумный выход из такой ситуации – скрыть результат выполнения команды.
Числовой формат вывода в явном виде задается с помощью инструкции format. В команде определения формата вывода после ключевого слова format указывается применяемый формат. Допустимые форматы, с кратким их описанием, перечислены в табл. 1.7.
Табл. 1.7. Числовые форматы (для инструкции format)
Формат |
Описание |
|
|
short |
Формат отображения числовых данных, при котором после де- |
сятичной точки отображается четыре цифры (формат данных |
|
|
с фиксированной точкой). Формат используется по умолчанию |
|
|
long |
Числовой формат, при котором после десятичной точки отобра- |
жается 7, 14 и 15 цифр в зависимости от типа числовых данных |
|
|
(формат данных с фиксированной точкой) |
|
|
short e |
Формат отображения числовых данных с мантиссой и показате- |
лем степени (формат данных с плавающей точкой), при котором |
|
|
после десятичной точки отображается четыре цифры |
|
|
|
Числовой формат отображения с мантиссой и показателем сте- |
long e |
пени (формат данных с плавающей точкой), при котором после |
десятичной точки отображается 7, 14 и 15 цифр в зависимости |
|
|
от типа числовых данных |
|
|
short g |
В зависимости от значения, для отображения применяется либо |
формат с плавающей точкой, либо с фиксированной точкой. По- |
|
|
сле десятичной запятой отображается четыре цифры |
|
|
long g |
В зависимости от значения, для отображения применяется либо |
формат с плавающей точкой, либо с фиксированной точкой. По- |
|
|
сле десятичной запятой отображается 7, 14 или 15 цифр |
|
|
short eng |
Инженерный формат с четырьмя отображаемыми цифрами по- |
сле десятичной точки и показателем степени, кратным трем |
|
|
|
long eng |
Инженерный формат с 7, 14 или 15 отображаемыми цифрами |
после десятичной точки и показателем степени, кратным трем |
|
|
|
+ |
Формат, при котором для положительных чисел отображается |
знак +, для отрицательных отображается знак -, а для нуля ото- |
|
|
бражается пробел |
bank |
Финансовый формат, при котором после десятичной точки ото- |
бражается две цифры |
|
|
|
hex |
Отображение чисел в шестнадцатеричной системе счисления |
rat |
Отображение чисел в виде рациональной дроби |
compact |
Режим отображения результатов вычислений в компактной фор- |
ме, с уменьшенными интервалами между строками |
|
|
|
loose |
Режим отображения результатов вычислений с увеличенными |
интервалами между строками. Используется по умолчанию |
|
|
|
39
Самоучитель Matlab
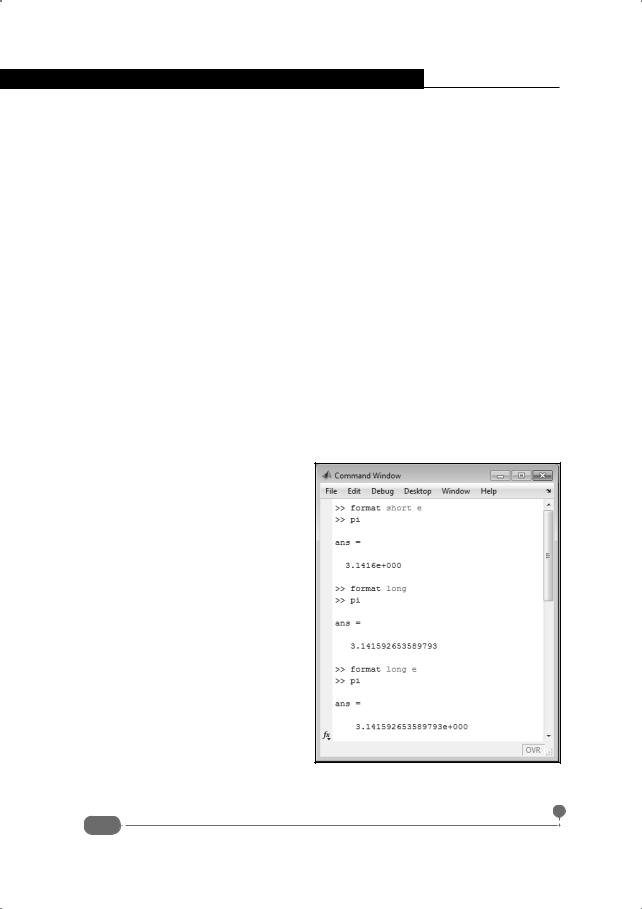
Ниже приведен пример отображения числа π в разных форматах (в командах использована встроенная константа Matlab pi, ввод пользователя выделен жирным шрифтом):
>>format short e
>>pi
ans = 3.1416e+000
>>format long
>>pi
ans = 3.141592653589793
>>format long e
>>pi
ans = 3.141592653589793e+000
>>format long eng
>>pi
ans = 3.14159265358979e+000
>>format bank
>>pi
ans = 3.14
>>format rat
>>pi
ans = 355/113
>>format +
>>pi
ans =
+
Эти же команды, выполненные в командном окне, представлены на рис. 1.9 и рис. 1.10.
Рис. 1.9. Применение различных форматов вывода (начальная часть командного окна)
40
