1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 4. Элементы матричной алгебры

Сначала создаем командой A=[1 2 1;-1 0 1;2 -1 1] матрицу, для которой затем вычисляем обратную матрицу. Используем команду B=inv(A), с помощью которой вычисляем обратную матрицу и результат записываем в переменную B. Свойства обратной матрицы проверяем, вычислив произведение A*B. В результате, как и следовало ожидать, получаем единичную матрицу.

При работе с матрицами часто приходится решать задачу о вычислении собственных чисел и собственных векторов матрицы. Собственные числа

имеет нетривиальное решение (то есть решение, отличное от тождественно нулевого).

На заметку

Собственные векторы определяются не однозначно, а с точностью до общего множителя. Обычно этот множитель выбирается так, чтобы вектор имел единичный модуль.

Собственные числа матрицы могут быть комплексными. Количество собственных чисел, с учетом их кратности, совпадает с рангом матрицы. Разным собственным числам отвечают разные собственные векторы. Для кратных собственных чисел количество независимых собственных векторов может быть в пределах от одного до кратности собственного числа.

Для вычисления собственных чисел и собственных векторов в Matlab используется функция eig(). Пример использования этой функции в разных вариантах вызова приведен в документе на рис. 4.10.

Сначала создаем матрицу A, а затем командой eig(A) вычисляем собственные числа матрицы. Стоит обратить внимание, что среди трех вычисленных собственных чисел матрицы два – комплексные. Результатом функции eig() в данном формате вызова возвращается вектор с элементами - собственными числами матрицы. Если результат вызова функции eig() записать в массив из двух элементов, то в первый элемент запишутся по столбикам собственные векторы матрицы-аргумента функции eig(), а во второй элемент записывается матрица, по диагонали которой располагаются соответствующие собственные числа (недиагональные элементы этой матрицы равны нулю). Примером может быть команда [x,l]=eig(A). В результате матрица x будет состоять из столбцов, которые являются собственными векторами матрицы A, а матрица l будет диагональной. Ее диагональные элементы являются собственными числами матрицы A. Для удобства ниже приведен код, который содержится в документе на рис. 4.10 (жирным шрифтом выделен ввод пользователя):

161

Самоучитель Matlab

Рис. 4.10. Вычисление собственных чисел

>> A=[1 2 1;-1 0 1;2 -1 1]

A =

>>eig(A) ans =

2.4883

-0.2442 + 1.7764i -0.2442 - 1.7764i

>>[x,l]=eig(A)

162

Глава 4. Элементы матричной алгебры

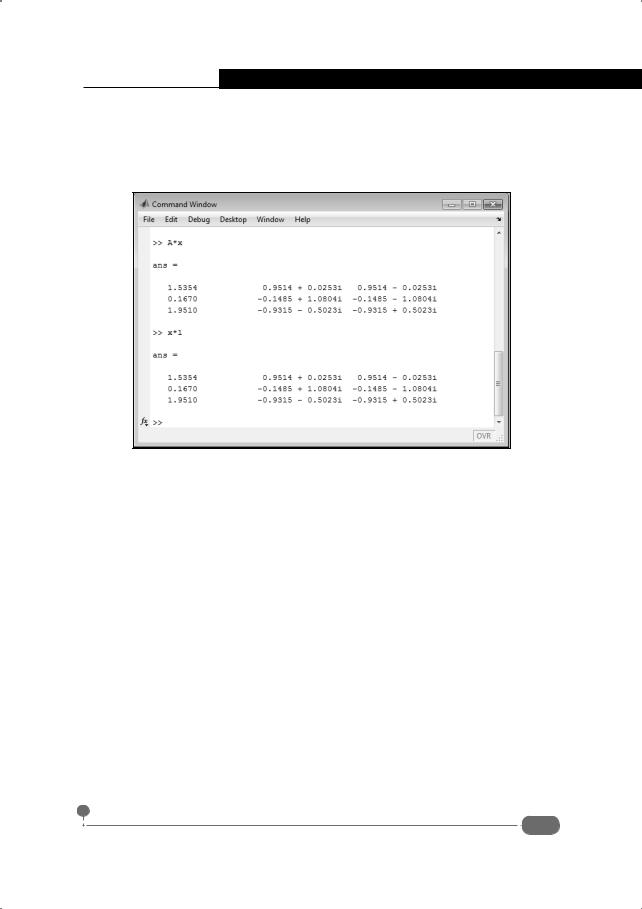
Вычисленные таким образом матрицы x, l и исходная матрица A должны быть такими (в силу определения собственных чисел и векторов), чтобы произведения A*x и x*l давали одинаковые результаты. Это обстоятельство мы проверяем во второй части рассмотренного ранее документа (см. рис. 4.10), представленной на рис. 4.11.

Рис. 4.11. Проверка результатов вычислений собственных чисел и собственных векторов

Как и следовало ожидать, результаты вычисления матриц A*x и x*l идентичны.

При работе с квадратными матрицами, кроме прочего, можно использовать операцию возведения в степень ^. Показатель степени может быть любым целым числом, в том числе и отрицательным. Примеры возведения матриц в целочисленные степени приведены в документе на рис. 4.12.

В некоторых случаях полезно прибегать к вычислению функций от матричных аргументов. При решении задач в аналитическом виде к такому подходу прибегают редко, поскольку для функции от матричного аргумента намного легче записать символьное выражение, чем получить приемлемое для прикладного использования выражение. Другое дело, когда для расчетов используется прикладной математический пакет, такой как Matlab. Ситуацию проиллюстрируем на примере вычисления матричной экспоненты.

Как известно, в Matlab есть встроенная функция exp() для вычисления экспоненты.

163

Самоучитель Matlab

Рис. 4.12. Возведение матрицы в степень

На заметку

По определению экспоненциальная функция для скалярного аргумента x опре-

Аргументом функции exp() можно указать матрицу. В этом случае результатом будет матрица, элементы которой получаются экспонированием со-

ответствующих элементов исходной матрицы. Так, если матрица ˆ состоит

A

из элементов aij (индексы i = 1,2,..,m и j = 1,2,...,n ) и она записана в переменную A, то в результате вычисления выражения exp(A) получим матрицу с элементами exp(aij ). По-другому вычисляется функция expm(A). Во-первых, матрица-аргумент A должна быть квадратной. Во-вторых, результатом является матрица, которая, если не вдаваться в подробности, вы-

вилу, что и экспонента от скалярного аргумента. Здесь через ˆ обозначена

E

единичная матрица того же ранга, что и матрица ˆ. Различие в функциях

A exp() и expm() иллюстрирует документ на рис. 4.13.

164

Глава 4. Элементы матричной алгебры

Рис. 4.13. Матричная экспонента

На первый взгляд может показаться, что польза от функции expm() и, более обще, матричных функций, которые вычисляются аналогично функциям скалярного аргумента, не очень велика. Но это не так. Рассмотрим простой, но показательный пример.

Допустим, что нам необходимо решить задачу Коши: систему диффе-

ма дифференциальных уравнений первого порядка, и для ее решения в аналитическом виде существуют стандартные приемы. Сложного в них ничего нет, но вычисление решения по общепринятому алгоритму может занять некоторое время. Поэтому простым, но длинным путем мы не пойдем. Отметим только, что точное решение данной систе-

165

Самоучитель Matlab

ответствующе решения на графике (а мы это увидим далее), то получим осциллирующие с затуханием функции.

Приведенное решение в числовом виде можно получить достаточно просто без использования специальных функций для решения систем дифферен-

и матрица коэффициентов правых частей системы дифференциальных

Затем воспользуемся формальной аналогией. Если бы у нас было не вектор-

ное уравнение, а скалярное df (t) = Af (t) с начальным условием f (0) = f0 , dt

то решение можно было бы записать практически сразу: f (t) = f0 exp(At) . Но у нас уравнение векторное, поэтому все операции в соответствующем выражении для решения следует понимать в смысле операций с матрицами.

решения в фиксированный момент времени t необходимо матрицу ˆ умно-

A

жить на скаляр t (выполняется поэлементное умножение). В результате по-

лучаем матрицу ˆ . Затем вычисляем матрицу ˆ (по правилу вычис-

At exp(At)

ления функции expm()) и умножаем ее (по правилу умножения матриц)

на вектор начальных значений f0 .

На заметку

Выше при построении решения для системы уравнений мы апеллировали к аналогии. Разумеется, аналогия не является критерием корректности метода. Тем не менее, можно убедительно доказать, что использованный метод верный.

Таким образом, процедура поиска решения ясна, и теперь ее можно автоматизировать – составить программный код, с помощью которого поиск решения системы из двух линейных дифференциальных уравнений первого порядка будет выполняться автоматически. Код соответствующей функции, которая называется ldes(), приведен ниже:

function [x y]=ldes(A,t,z) N=length(t);

166

Глава 4. Элементы матричной алгебры

for i=1:N M=expm(A*t(i));

x(i)=z(1)*M(1,1)+z(2)*M(1,2);

y(i)=z(1)*M(2,1)+z(2)*M(2,2); end

end

Аргументов у функции три: матрица коэффициентов A, список значений аргумента t (узловые точки), в которых вычисляются значения искомых функций, а также вектор начальных значений функций z. Результат вычисления функции записывается в массивы x и y, каждый из которых представляет набор точек-значений соответственно первой x(t) и второй y(t) искомых функций в узловых точках.

Командой N=length(t) определяется количество узловых точек, для которых необходимо вычислить значения функций. Затем запускается оператор цикла, в котором индексная переменная i пробегает значения от 1 до N. На каждой итерации определяются значения искомых функций в соответствующей узловой точке. Так, при фиксированном значении индексной переменной командой M=expm(A*t(i)) вычисляется матричная экспонента (для данного момента времени t(i)). Затем командами x(i)=z(1)*M(1,1)+z(2)*M(1,2) и y(i)=z(1)*M(2,1)+z(2)*M(2,2)

вычисляются значения функций в узловой точке.

На заметку

При вычислении произведения матрицы M на вектор-столбец начальных условий z получаем вектор-столбец. Первый элемент этого вектора-столбца дает значение функции x(t) в узловой точке (элемент x(i)). Второй элемент вектора-столбца дает значение функции y(t) в узловой точке (элемент y(i)). Чтобы получить первый элемент вектора-столбца, необходимо перемножить и сложить соответствующие элементы первой строки матрицы M и элементы вектора начальных значений z. Первая строка матрицы M – это элементы M(1,1) и M(1,2). Первый элемент вектора начальных значений – это z(1), а второй элемент вектора начальных значений – это z(2). В результате получаем комбинацию z(1)*M(1,1)+z(2)*M(1,2). Аналогично вычисляется второй элемент вектора-столбца: перемножаются и суммируются элементы второй строки матрицы M и элементы вектора начальных значений. Желающие могут подумать, как тот же алгоритм можно было бы реализовать с использованием операции матричного произведения вместо явного выписывания сумм и произведений.

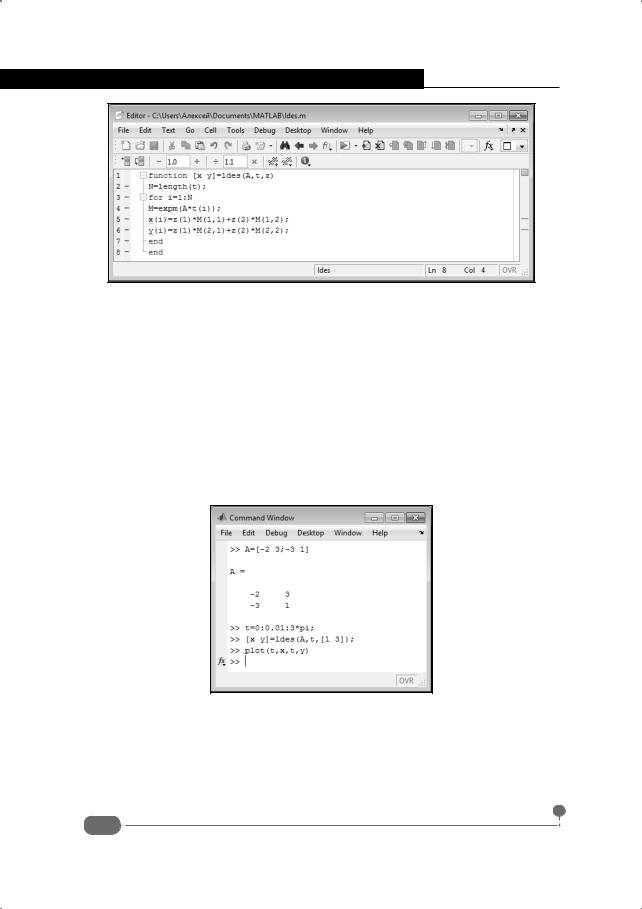
Окно редактора m-файлов с кодом функции ldes() показано на рис. 4.14.

После того, как функция ldes() создана, ее можно использовать для решения системы дифференциальных уравнений. В командном окне вводим следующие команды (жирным шрифтом выделен ввод пользователя):

167

Самоучитель Matlab

Рис. 4.14. Редактор m-файлов с кодом функции для вычисления решения дифференциального уравнения

>> A=[-2 3;-3 1]

A =

-2 3 -3 1

>>t=0:0.01:3*pi;

>>[x y]=ldes(A,t,[1 3]);

>>plot(t,x,t,y)

Здесь командой A=[-2 3;-3 1] создается матрица коэффициентов, командой t=0:0.01:3*pi формируется набор узловых точек, а затем командой [x y]=ldes(A,t,[1 3]) находим решение системы дифференциальных уравнений. Командное окно с кодом приведено на рис. 4.15.

Рис. 4.15. Командное окно с кодом для вычисления решения дифференциального уравнения

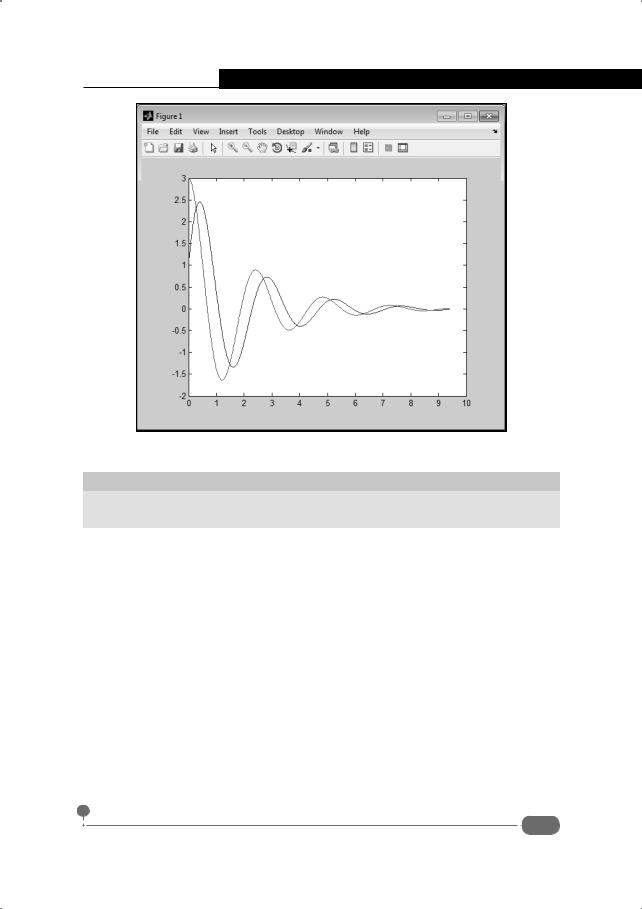
В результате выполнения команды plot(t,x,t,y) создается график для функциональных зависимостей x(t) и y(t), полученных в результате решения системы дифференциальных уравнений. Графики функций x(t) и y(t) представлены на рис. 4.16.

168

Глава 4. Элементы матричной алгебры

Рис. 4.16. Графическое представление для найденного решения

На заметку

Графики функций строятся на интервале от 0 до 3π. Наличие числа π здесь является чистой формальностью и никакой особой смысловой нагрузки не несет.

Преобразование матриц

Этого объяснить я Вам не могу, потому что сам толком ни черта не понимаю.

К/ф "Семнадцать мгновений весны"

В этом разделе речь пойдет о некоторых специфических операциях, которые относятся скорее к использованию матриц не как математических объектов, а как массивов данных. Понятно, что вариантов здесь может быть очень много. Для большинства из них в Matlab есть специальные функции. Мы остановимся только на наиболее интересных моментах.

Достаточно часто приходится создавать так называемые блочные матрицы, которые можно представить как такие, что состоят из матричных блоков. Другими словами, элементами блочной матрицы являются матрицы. Примеры приведены в документе на рис. 4.17.

169

Самоучитель Matlab

Рассмотрим следующий командный код более внимательно (жирным шрифтом выделен ввод пользователя):

>> E=eye(2)

E =

10

01

>>O=zeros(2)

O =

00

00

>>U=ones(2)

U =

11

ты нулевые). Функцией zeros() создается матрица с нулевыми элементами, а функцией ones() создается матрица, все элементы которой единичные. Размер матрицы указывается аргументом перечисленных функций. Таким образом, создается три матрицы размерами 2×2 каждая: единичная матрица E, нулевая матрица O и матрица из единиц U. Затем командой A=[E,2*U;3*U,O] создается блочная матрица A. Если посмотреть на эту команду формально, то речь идет о создании матрицы 2×2. Однако элементы матрицы сами являются матрицами. Причем матрица U при передаче элементом в блочную матрицу предварительно умножается на число. В результате получаем матрицу A, которая имеет размеры 4×4. Ее левый верхний блок – это матрица E. Верхний правый блок – матрица, состоящая из двоек (результат умножения матрицы U на 2). Левый нижний блок – матрица, состоящая из троек (результат умножения матрицы U на 3). Правый нижний блок – нулевая матрица O.

170