1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 6. Интегрирование и дифференциальные уравнения

На заметку

Для уравнения первого порядка указание не только начального значения для функции, но еще и производной означает переизбыток информации. Поэтому все эти параметры должны быть согласованы: если в выражение, определяемое функцией - первым аргументом функции ode15i(), подставить начальное значение независимого аргумента, функции и ее производной, выражение должно быть равно нулю. Здесь указаны значения y(0) = 1 и y′(0) = 0 , что

находится в полном согласии с выражением (y′ y)2 −x2 = 0 при x = 0 .

В результате выполнения команды [x,y]=ode15i(f,0:0.1:1.5,1,0)

в переменную x записывается список значений аргумента функции на интервале от 0 до 1.5, а в переменную y записываются значения вычисляемой функции в соответствующих точках. Полученная функциональная зависимость отображается графически командой plot(x,y,'b-', 'LineWidth',2) (сплошная синяя линия). Для сравнения приводится

кривая для функции y(x) = 1 + x2 , являющейся аналитическим решением исходного уравнения. В этом случае используем команду plot(x, sqrt(1+x.^2),'r:','LineWidth',3) (красная пунктирная линия). Командное окно с инструкциями для решения неявного дифференциального уравнения показано на рис. 6.21.

Рис. 6.21. Решение неявного дифференциального уравнения

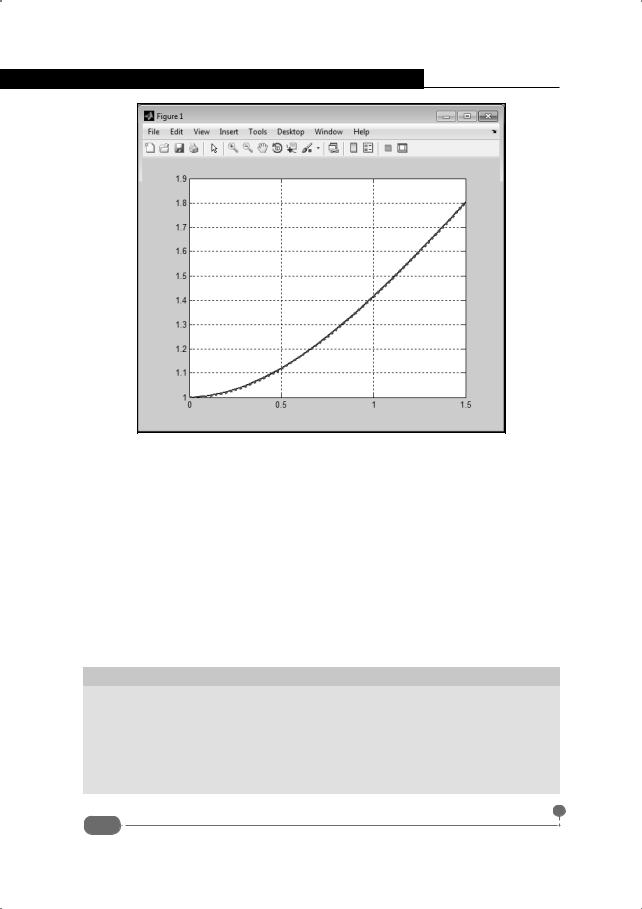
График для полученного решения представлен на рис. 6.22.

Стоит отметить два обстоятельства. Во-первых, кривые для аналитического и числового решений практически совпадают. Во-вторых, в процессе поиска решения мы не получили никакого намека на второе решение. Хотя оно в данном случае для всего интервала аргумента от 0 до 1.5 не подходит, оно все же существует. К сожалению, ситуация типична для нелинейных уравнений (а именно к таким уравнениям обычно относятся неявные дифференциальные уравнения). При наличии нескольких независимых решений для их поиска приходится применять более изощренные методы, чем вызов встроенной функции.

261

Самоучитель Matlab

Рис. 6.22. Графическое представление для решения неявного дифференциального уравнения

Краевые задачи

Меня не проведешь. Приемы сыщиков я вижу на пять футов вглубь.

К/ф "Приключения Шерлока Холмса и доктора Ватсона. Собака Баскервилей"

При решении краевой задачи условия на функцию и/или производные задаются в разных точках – на границах некоторого интервала. Несмотря на кажущуюся незначительность этого отличия по сравнению с задачей Коши, ситуация меняется качественно. Причем настолько, что для решения краевой задачи используются совершенно другие алгоритмы.

На заметку

Краевая задача подразумевает наличие как минимум двух условий, что автоматически означает, что порядок дифференциального уравнения должен быть не ниже второго. Другими словами, краевая задача для дифференциального уравнения первого порядка не ставится. При этом решение краевой задачи подразумевает сведение уравнения (системы уравнений) высокого порядка к системе уравнений первого порядка. Поэтому в этом разделе мы будем фактически рассматривать краевые задачи для систем уравнений первого порядка.

262

Глава 6. Интегрирование и дифференциальные уравнения

зуются встроенные функции bvp4c() и bvp5c(). Функции практически идентичны. Главное различие заключается в способе контроля ошибок

dx

ции bvp5c() контролируется реальная погрешность вычисления вектор-

ной функции y(x) . Аргументы функциям bvp4c() и bvp5c() передаются схожим образом. Так, первый и второй аргументы функций bvp5c() и bvp4c() передаются в виде указателей на функции, которые соответственно определяют решаемое уравнение (систему уравнений) и граничные условия. Рассмотрим некоторые простые примеры.

Решим следующую краевую задачу: дифференциальное уравнение второго порядка y′′(x) −y(x) + 2x = 0 с граничными условиями y(0) = 0 и y(1) = −1 . Задача имеет аналитическое решение y(x) = 2x − 3sh(x) sh(1). Для решения этой задачи в Matlab сводим дифференциальное уравнение второго порядка к системе уравнений первого порядка: y′(x) = z(x) и z′(x) = y(x) −2x . Граничные условия в общем случае также следует записать в новых обозначениях, но в данном случае граничные условия остаются неизменными: y(0) = 0 и y(1) = −1 . После этого можно приступить к процессу поиска решения краевой задачи в Matlab. В первую очередь

dx

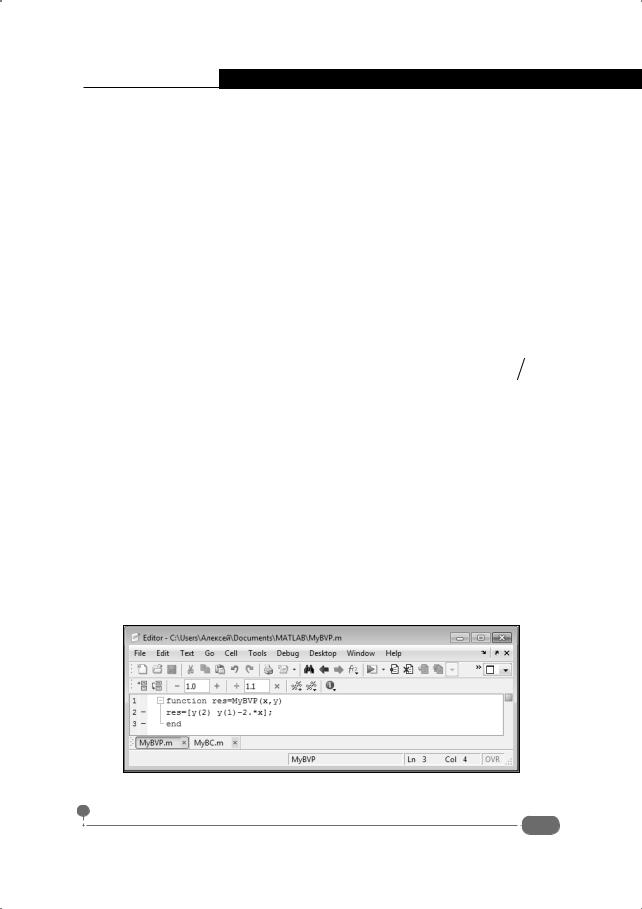
function res=MyBVP(x,y) res=[y(2) y(1)-2.*x]; end

Окно с кодом функции показано на рис. 6.23.

Рис. 6.23. Программный код функции, определяющей систему уравнений

263

Самоучитель Matlab

На заметку

Обратите внимание, что вектор-функция для системы уравнений определяется в виде вектора-строки, а не вектора-столбца, как это было при решении задачи Коши. Но это не принципиально.

Кроме функции, определяющей систему уравнений, необходимо задать еще и функцию, которая определяет граничные условия. Функция для определения граничных условий должна соответствовать таким критериям. У нее два аргумента. Первый аргумент является вектором значений функций системы на левой границе, а второй аргумент является вектором значений функций системы на правой границе. В качестве значения функцией, определяющей граничные условия, возвращается список с элементами, каждый из которых определяет граничное условие. Эти элементы представляют собой выражения, в которые входят значения функций на соответствующей границе. Чтобы получить граничное условие, необходимо приравнять выражение к нулю.

На заметку

Обычно в граничные условия входят неизвестные функции и/или их производные. При этом максимально возможная степень производной в граничных условиях на единицу меньше максимальной степени производной, входящей в уравнение. Поэтому если уравнение/система сводится путем введения новых функций к системе уравнений первого порядка, граничные условия будут содержать только функции, но не их производные.

Для данной задачи функция, определяющая граничные условия, задается в таком виде:

function res=MyBC(ya,yb) res=[ya(1) yb(1)+1];

end

У функции, как и указывалось выше, два аргумента, которые обозначены как ya и yb. Первый аргумент ya представляет собой список значений искомых функций на левой границе интервала поиска решения. Второй аргумент yb представляет собой список значений искомых функций на правой границе интервала поиска решения. Ссылки ya(1) и yb(1) означают первую функцию в системе уравнений (в данном случае это y(x)) соответственно на левой и правой границах. Ссылки ya(2) и yb(2) означают вторую функцию в системе уравнений (в данном случае это z(x) ) соответственно на левой и правой границах. В качестве результата возвращается список из двух элементов: ya(1) и yb(1)+1. Первый элемент означает равенство нулю выражения ya(1), то есть условие y(x) = 0 на левой границе. Второй элемент означает равенство нулю выражения yb(1)+1, то есть условие y(x) +1 = 0 на правой границе. Окно с кодом функции, задающей граничные условия, показано на рис. 6.24.

264

Глава 6. Интегрирование и дифференциальные уравнения

Рис. 6.24. Функция для определения граничных условий

После этого можно переходить к решению краевой задачи. На рис. 6.25 показано командное окно с инструкциями, позволяющими найти это решение.

Рис. 6.25. Команды для вычисления решения краевой задачи

В первую очередь определяется начальное распределение для искомых функций. Дело в том, что в алгоритме решения краевой задачи важно знать "хорошее" (или не очень) приближение для искомой функции или функций. Именно такое начальное приближение нужно создать для набора функций, используемых в уравнении. Причем реализуется все это в виде специальной структуры.

На заметку

Структуры кратко обсуждаются в Приложении Б.

Структура, в свою очередь, создается с помощью встроенной функции bvpinit(). Нужная нам структура возвращается функцией bvpinit() в качестве результата. Аргументом этой функции передаются два списка. Первый определяет набор узловых точек по независимой переменной, а второй является списком начальных приближений каждой из неизвестных функций в узловых точках. Есть разные способы передать аргументы функции bvpinit(). В рассматриваемом примере список узловых точек независимой переменной формируется с помощью еще одной встроенной функции linspace(). Функцией создается список значений. У функции три аргумента: начальное

265

Самоучитель Matlab

и конечное значение для элементов списка и количество этих элементов. Создается список равномерно распределенных элементов. Например, командой linspace(0,1,10) создается список из десяти элементов с первым элементом 0 и последним элементом 1, шаг дискретности равен 0.1. Вся команда по созданию структуры с начальным распределением для искомых функций имеет вид IC=bvpinit(linspace(0,1,10),[-2 0]). Результат записывается в переменную IC, а вторым аргументом функции bvpinit() передается список [-2 0]. В этом случае для первой функции во всех узловых точках используется значение -2, а для второй функции во всех узловых точках используется значение 0. После этого командой sol=bvp4c('MyBVP','MyBC',IC) решаем краевую задачу. Вся последовательность команд выглядит так:

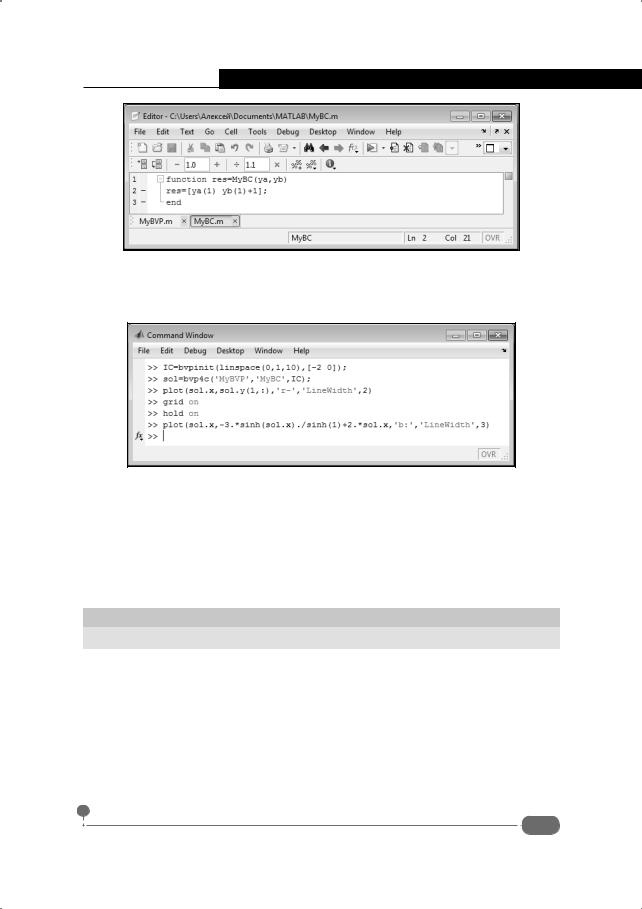
>>IC=bvpinit(linspace(0,1,10),[-2 0]);

>>sol=bvp4c('MyBVP','MyBC',IC);

>>plot(sol.x,sol.y(1,:),'r-','LineWidth',2)

>>grid on

>>hold on

>>plot(sol.x,-3.*sinh(sol.x)./sinh(1)+2.*sol.x,'b:','LineWidth',3)

Результат вызова функции bvp4c() записывается в переменную sol. Это структура, и у нее несколько полей. Поле x (полная ссылка на это поле имеет вид sol.x) содержит набор узловых точек. Поле y (полная ссылка на это поле имеет вид sol.y) содержит значения искомых функций в узловых точках. Значенияпервойфункциисодержатсявстрокеsol.y(1,:)(функция y(x)), для второй функции значения содержатся в строке sol.y(2,:) (функция z(x) ).Поэтомучтобыпостроитьграфикдлявычисленнойфункции,можноиспользовать команду plot(sol.x,sol.y(1,:),'r-','LineWidth',2)

(красная линия толщины 2). Для сравнения строится кривая аналитического решения командой plot(sol.x,-3.*sinh(sol.x)./sinh(1)+2.* sol.x,'b:','LineWidth',3) (синяя пунктирная кривая). На рис. 6.26 показан результат создания кривых для аналитического решения и решения, вычисленного числовыми методами.

Как и во всех предыдущих случаях, совпадение числового и аналитического результатов более чем приемлемое.

Для разнообразия решим еще одну краевую задачу, но уже с использованием функции bvp5c() и с несколько иным способом передачи аргумен-

тов. Задача формулируется так: решить дифференциальное уравнение y′′(x) −y′(x) = 0 с граничными условиями y(0) = −1 и y′(1) −y(1) = 2 .

Задача имеет решение y(x) = exp(x) −2 . Общая схема решения стандартная: сводим задачу к системе уравнений первого порядка, создаем функции для системы уравнений и граничных условий, начальное распределение и затем с помощью встроенной функции находим решение.

266

Глава 6. Интегрирование и дифференциальные уравнения

Рис. 6.26. Графическое представление для решения краевой задачи

торая определяет функцию для правой части системы уравнений.

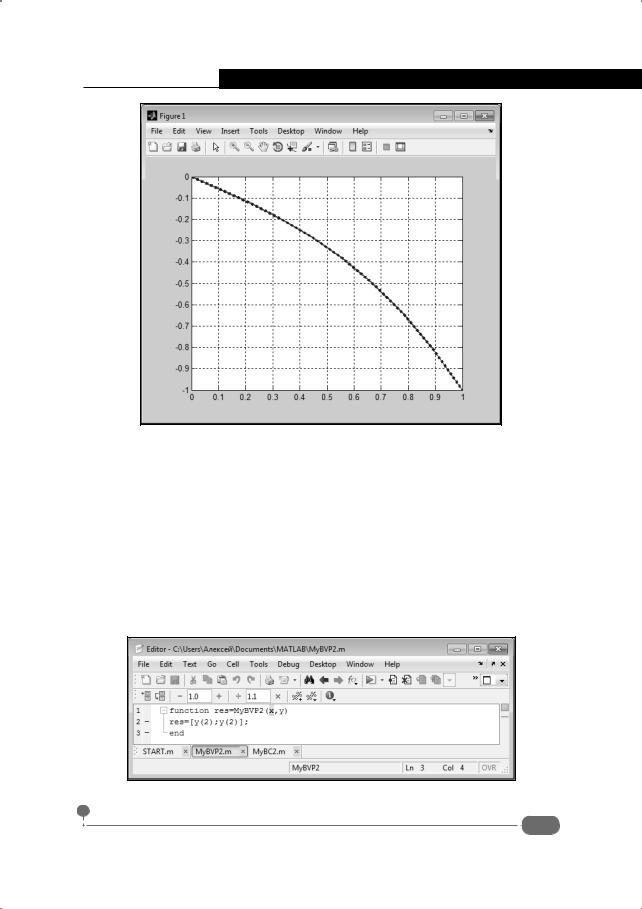
function res=MyBVP2(x,y) res=[y(2);y(2)];

end

Код достаточно простой и, думается, особых комментариев не требует. На рис. 6.27 этот же код представлен в окне редактора m-файлов.

Рис. 6.27. Функция для определения системы уравнений

267

Самоучитель Matlab

Функция для определения граничных условий такая:

function res=MyBC2(ya,yb) res=[ya(1)+1;yb(2)-yb(1)-2]; end

Код функции в окне редактора m-файлов представлен на рис. 6.28.

Рис. 6.28. Функция для определения граничных условий

В обоих случаях функции возвращают в качестве результата векторстолбец. Кроме этого, для формирования начального распределения для искомых функций создаем специальную функцию START(), которая в качестве результата возвращает вектор-строку с двумя элементами:

function res=START(x) res=[x.^2/2+x-1,x+1]; end

приближение для функции y(x)). Второй элемент соответствует функции y2(x) = x +1 (начальное приближение для производной y′(x) = x +1). Окно редактора m-файлов с кодом этой функции можно наблюдать на рис. 6.29.

Рис. 6.29. Функция для определения начального распределения

268

Глава 6. Интегрирование и дифференциальные уравнения

Рис. 6.30. Команды для решения краевой задачи

Рис. 6.31. Графическое представление для полученного решения

Далее используем следующую последовательность команд для решения краевой задачи:

>>IC2=bvpinit(0:0.01:1,@START);

>>sol=bvp5c(@MyBVP2,@MyBC2,IC2);

>>plot(sol.x,sol.y(1,:),'r-','LineWidth',2)

>>grid on

>>hold on

>>plot(sol.x,exp(sol.x)-2,'b:','LineWidth',3)

Инструкцией IC2=bvpinit(0:0.01:1,@START) создается начальное приближение для искомых функций. Первым аргументом функции bvpinit()

269

Самоучитель Matlab

передается список, формируемый командой 0:0.01:1. Вторым аргументом передается указатель @START на функцию, которой вычисляется начальное распределение для искомых функций. Далее это начальное условие, вместе с указателями @MyBVP2 и @MyBC2 на функцию уравнения и граничных условий, используется в команде sol=bvp5c(@MyBVP2,@MyBC2,IC2) для решения краевой задачи. Окно с использованными командами показано на рис. 6.30.

Как обычно, полученный результат отображается графически вместе с кривой для аналитического решения (рис. 6.31).

Традиционно кривая, построенная на основе числового решения, совпадает с кривой, построенной на основе известной зависимости для точного (аналитического) решения.

Завершающий пример

Да не было ничего! Все это происки!

В. Черномырдин

Еще один простой, но полезный пример использования встроенных функций для решения дифференциальных уравнений рассмотрим в этом разделе. Речь идет о том, что при определении некоторой функции используется функция для решения дифференциального уравнения. Другими словами, функция определяется так, что при вычислении результата решается дифференциальное уравнение. Обратимся к нижеприведенному коду:

>>f=@(x,y)(2*y./x+2*x.^3);

>>F=@(x,a,ya)(ode45(f,a:(x-a)/100:x,ya));

>>[x,y]=F(3,1,0);

>>plot(x,y,'r-','LineWidth',2)

>>grid on

>>hold on

>>plot(x,x.^2.*(x.^2-1),'b:','LineWidth',3)

Командой f=@(x,y)(2*y./x+2*x.^3) определяется функция, задающая

правую часть дифференциального уравнения y′(x) = 2 y(x) + 2x3 . Общее x

решение уравнения имеет вид y(x) = x2(x2 +C). Константа C вычисляется исходя из начальных условий.

Командой F=@(x,a,ya)(ode45(f,a:(x-a)/100:x,ya)) определяется функция, в которой вычисляется решение для упомянутого выше уравнения с начальным значением ya (третий аргумент функции F), которое вычисляется в точке a (второй аргумент функции F). Значения для решения дифференциального уравнения вычисляются от начального значения независимой переменной до того, что передано первым аргументом функции F.

270