1-2 Моделирование / Matlab. Практический подход. Самоучитель

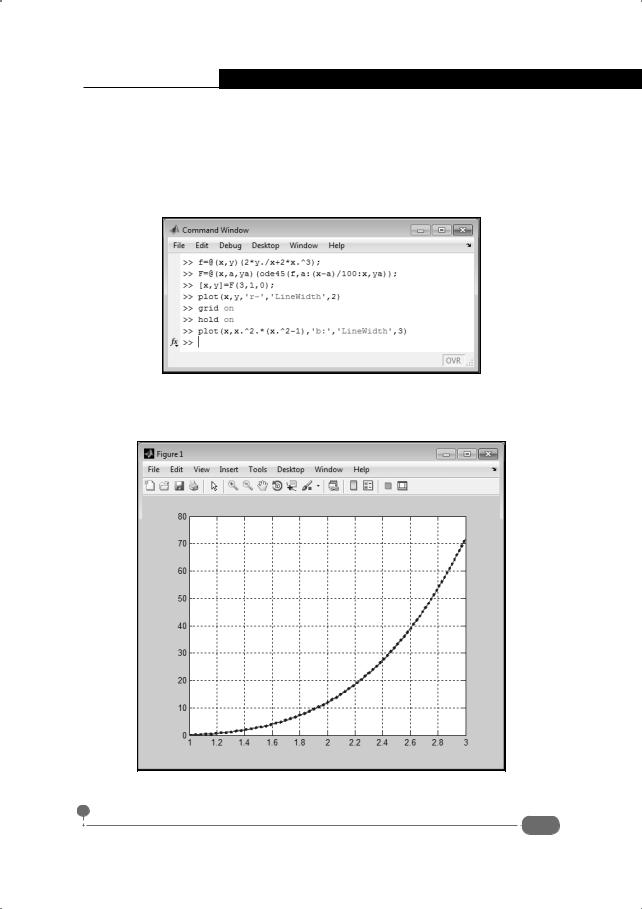
Глава 6. Интегрирование и дифференциальные уравнения

Результатом возвращается, как и в случае функции ode45(), список узловых точек независимой переменной и значений функции в этих точках.

Примером использования созданной функции служит команда [x,y]=F(3,1,0).Вданномслучаевычисляетсярешениеy(x) = x2(x2 −1) . Полученный результат проверяется графически. На рис. 6.32 показано командное окно с соответствующими инструкциями.

Рис. 6.32. Использование функции решения дифференциального уравнения при определении анонимной функции

На рис. 6.33 представлен график для рассчитанной функции.

Рис. 6.33. График построен на основе результатов решения дифференциального уравнения

271

Самоучитель Matlab

Как и во всех предыдущих случаях, мы на фоне числового решения отобразили кривую для аналитического решения.

Существуют и другие способы использования функции для решения дифференциальных уравнений. Заинтересованный в этом вопросе читатель может проявить здесь свою изобретательность.

272

Глава 7 Уравнения математической физики

- Вы уже думаете об этом деле? - У меня оно не выходит из головы. - Какие Ваши соображения?

- Запутанная история! - Как это верно, Ватсон!

К/ф "Приключения Шерлока Холмса и доктора Ватсона. Собака Баскервилей"

С математической точки зрения уравнения математической физики – это дифференциальные уравнения в частных производных второго порядка. Такого типа уравнения описывают ряд важных физических процессов – отсюда, собственно, и название. Сразу следует отметить, что возможности по аналитическому решению уравнений математической физики существенно ограничены, поэтому решение этих уравнений в числовом виде нередко является единственно возможным выходом из ситуации.

В отличие от обыкновенных дифференциальных уравнений, при решении уравнения в частных производных (второго порядка) самого этого уравнения мало для получения решения.

На заметку

В уравнениях математической физики независимые переменные, равно как и сама искомая функция, обычно имеют четкую физическую интерпретацию. Как правило, выделяют пространственные переменные и переменную, обозначающую время (для описания процессов, зависящих от времени). В зависимости от наличия переменной времени, порядка производной по этой переменной (по пространственным переменным производные второго порядка) и способа вхождения в уравнение, выделяют несколько типов уравнений. Уравнения гиперболического типа содержат вторую производную по времени и описывают колебания струн и мембран. Уравнения параболического типа содержат первую производную по времени и описывают процессы теплообмена и диффузии вещества в пространстве. Уравнения эллиптического типа не содержат производных по времени и описывают распределение электростатического поля или стационарное (установившееся) распределение температуры. Разумеется, этими задачами применимость уравнений математической физики не исчерпывается.

Принципиально важно знать область, для которой ищется решение, а также граничные и начальные условия. Более того, не имея информации об области и граничных условиях, вообще нет смысла говорить о решении уравнений в частных производных второго порядка. Даже незначительное, на первый взгляд, изменение граничных условий может привести к кардинальному изменению в решении. Неудивительно, что в такой ситуации

273

Самоучитель Matlab

желательно иметь эффективное и надежное средство, позволяющее относительно быстро и просто получать решение. Дальше мы попытаемся убедить читателя, что Matlab как раз является таким средством.

На заметку

В Matlab для решения уравнений в частных производных есть пара встроенных функций и пакет инструментов Partial Differential Equation Toolbox. Встроенные функции позволяют решать уравнения для случая, когда уравнение содержит одну пространственную переменную (одномерная задача). С практической точки зрения это не самый важный тип задач. Намного более эффективным представляется использование пакета инструментов. Кроме того, в главе будет показано, насколько полезно приложение Matlab в случае, если удается найти точное (аналитическое) решение задачи.

Одномерный случай

А это не химера, с физическими формулами. То, что произошло сегодня, было непредвиденным и не укладывалось ни в одно, ни в другое решение.

К/ф "Семнадцать мгновений весны"

Функция pdepe() позволяет решать одномерные уравнения параболического и эллиптического типа достаточно общего вида. У функции несколько аргументов. Первый аргумент может принимать три целочисленных значения (0, 1 или 2). Этот аргумент определяет систему координат, в которой вычисляется пространственная производная. Значение 0 соответствует декартовым координатам, значение 1 соответствует полярным координатам, а значение 2 соответствует сферическим координатам. В последних двух случаях подразумевается, что искомая функция зависит только от одной пространственной координаты (радиуса - соответственно в полярной или сферической системе координат).

На заметку

"Классическое" уравнение параболического типа в одномерном случае в декар-

товых координатах имеет вид ∂u(t,x) = a2 ∂2u(t,x) , где a - параметр задачи,

∂t ∂x2

переменная t означает время, переменная x есть пространственная координата, а u(t,x) - неизвестная (искомая) функция от времени и координаты. В полярных координатах (радиус r и угол ϕ ) для функции, которая не зависит от угла

274

Глава 7. Уравнения математической физики

В сферических координатах (радиус r и углы ϕ и θ ) для функции, не зависящей

ввести обобщенную пространственную координату z , то все три уравнения

менная n может принимать значение n = 0 для декартовых координат, n = 1 для полярных координат и n = 2 для сферических координат. Фактически, параметр n передается первым аргументом функции pdepe().

Следует также отметить, что все три уравнения являются частным случаем бо-

∂u(t,r )

лее общего уравнения для трехмерного случая ∂t = a2∆u(t,r ) , где че-

рез ∆ обозначен оператор Лапласа, записанный в соответствующей системе

координат. Через вектор r обозначен полный набор пространственных координат.

Уравнения эллиптического типа обычно рассматривают в виде ∆u(t,r ) = f (r ) , где функция f (r ) известна. Однако для одномерного случая уравнение содержит производные от неизвестной функции только по одной (пространственной) переменной и является, таким образом, обыкновенным дифференциальным уравнением. Поэтому особого интереса в данном случае уравнение эллиптического типа не представляет.

Помимо первого аргумента, определяющего пространственную симметрию задачи, аргументами функции pdepe() также передаются: указатель на функцию, определяющую решаемое уравнение (систему уравнений), указатель на функцию начального распределения, указатель на функцию граничных условий, список узловых значений по переменной времени и список узловых значений по пространственной переменной. В качестве результата (первое значение из списка возвращаемых значений) функцией pdepe() возвращается трехмерный массив, который содержит значения каждой функции системы (в общем случае) уравнений в каждой из узловых точек по времени и координате. Все перечисленные функции, которые упоминались выше, должны иметь определенную структуру.

Для лучшего понимания, что и как определяется при решении уравнения параболического типа в одномерном (по пространственной переменной) случае, следует учесть, что функция pdepe() позволяет решать уравнения

275

Самоучитель Matlab

Здесь через u(x,t) обозначена неизвестная функция, которую следует вычислить. Частные производные по времени и пространственной координа-

случае от пространственной координаты, времени, неизвестной функции и частной производной от этой функции по пространственной координате. Определив эти три функции, мы однозначно задаем вид решаемого уравнения. Но этого все равно мало. Необходимо еще задать граничные и начальные условия. С начальным условием проще – это значение неиз-

границ. Поэтому чтобы задать граничные условия, необходимо определить функции p(x,t,u ) и q(x,t) отдельно на левой и правой границе. Таким образом, чтобы приступить к решению задачи, необходимо определить функ-

ции уравнения. Функция уравнения – та функция, которая передается вторым аргументом функции pdepe(). Функция уравнения принимает такие аргументы и в таком порядке: пространственная независимая переменная, переменная времени, неизвестная функция (относительно которой решается уравнение) и производная от искомой функции по пространственной координате. В качестве результата функцией уравнения возвращается список из

Для определения функции уравнения достаточно знать уравнение.

На заметку

276

Глава 7. Уравнения математической физики

Общий синтаксис объявления функции уравнения имеет следующий вид:

function [C,F,S]=имя_функции(x,t,u,du)

%здесь код функции

%x – пространственная переменная

%t - время

%u - искомая функция

%du - производная от искомой функции по пространственной координате end

Функция начального распределения зависит только от пространственной координаты и определяет зависимость f (x). Указатель на эту функцию передается третьим аргументом функции pdepe().

Функция для определения граничных условий имеет пять аргументов: значение пространственной переменной на левой границе, значение искомой функции на левой границе, значение пространственной переменной на правой границе, значение искомой функции на правой границе, переменная времени. В качестве результата возвращается список из четырех элементов: значение функции p(x,t,u ) на левой границе, значение функции q(x,t) на левой границе, значение функции p(x,t,u ) на правой границе и значение функции q(x,t) на правой границе.

На заметку

При решении физических задач обычно рассматривают три типа граничных условий:

1.Граничное условие первого рода (условие Дирихле), когда на границе задано значение искомой функции.

2.Граничное условие второго рода (условие Неймана), когда на границе задано значение производной от искомой функции.

3.Граничное условие третьего рода, когда на границе задается значение линейной комбинации функции и ее производной по пространственной координате.

Граничные условия в общем случае зависят от времени.

Для начала рассмотрим простой пример. Решим задачу об остывании тонкого стержня длины L с коэффициентом теплопроводности a2 , если в начальный момент центральная треть стержня нагрета до температуры T0 , а остальная часть стержня в начальный момент имеет нулевую температуру.

277

Самоучитель Matlab

На левой границе постоянно поддерживается нулевая температура, а правый конец стержня теплоизолированный.

Сформулируем задачу математически. Для этого обозначим через T(z, τ)

L 3 ≤ z ≤ 2L 3 и T(z, τ = 0) = 0 в противном случае. Граничные усло-

ство нулю производной на правой границе) является следствием теплоизолированности стержня справа. Теплоизолированность означает отсутствие теплового потока, который пропорционален производной от температуры по координате.

Задача содержит достаточно много феноменологических параметров. Для решения задачи нужно либо задать числовые значения для этих параметров, либо обезразмерить задачу. В последнем случае количество параметров, которые необходимо задать, существенно сокращается.

Вводим новые обозначения: новая безразмерная пространственная координата x = z L (0 ≤ x ≤ 1), новое безразмерное время t = a2τ L2 и новая

с начальным условием u(x,t = 0) = 1 при 1 3 ≤ x ≤ 2 3 и u(x,t = 0) = 0 в противном случае. Граничные условия имеют вид u(x = 0,t) = 0 и

∂u(x = 1,t) = 0 . Таким образом, можем приступить к решению задачи.

∂x

Для этого создаем функцию уравнения:

function [C,F,S]=PDEfunc(x,t,u,du) C=1;

F=du;

S=0; end

У функции PDEfunc(), как и положено, четыре аргумента, а результатом является список из трех элементов. Командой C=1 определяется выражениемножитель для производной по времени в левой части уравнения (это единица). Командой F=du задается дифференцируемое по пространственной переменной выражение в правой части уравнения (это частная произво-

278

Глава 7. Уравнения математической физики

дная первого порядка по пространственной координате). Поскольку тепловые источники отсутствуют, командой S=0 определяем соответствующее слагаемое в правой части как нулевое. Код функции PDEfunc() в окне редактора m-файлов показан на рис. 7.1.

Рис. 7.1. Код функции уравнения

Функция, которая определяет начальное распределение температуры, называется PDEinit(), у нее один аргумент и она возвращает скалярное значение в качестве результата:

function f=PDEinit(x) f=(x>=1/3)&(x<=2/3); end

Здесь мы воспользовались тем обстоятельством, что логическое значение истина обрабатывается как единица, а логическое значение ложь обрабатывается как ноль. Поэтому функция PDEinit() в качестве результата возвращает значение 1, если для ее аргумента выполнено условие x>=1/3 и одновременно x<=2/3. Здесь мы использовали оператор логического и &. В противном случае возвращается 0. На рис. 7.2 показано окно редактора m-файлов с кодом функции.

Рис. 7.2. Код функции начального условия

279

Самоучитель Matlab

Еще одна функция создается для того, чтобы задать граничные условия. Эта функция называется PDEbound() и имеет такой код:

function [p0,q0,p1,q1]=PDEbound(x0,u0,x1,u1,t) p0=u0;

q0=0;

p1=0;

q1=1; end

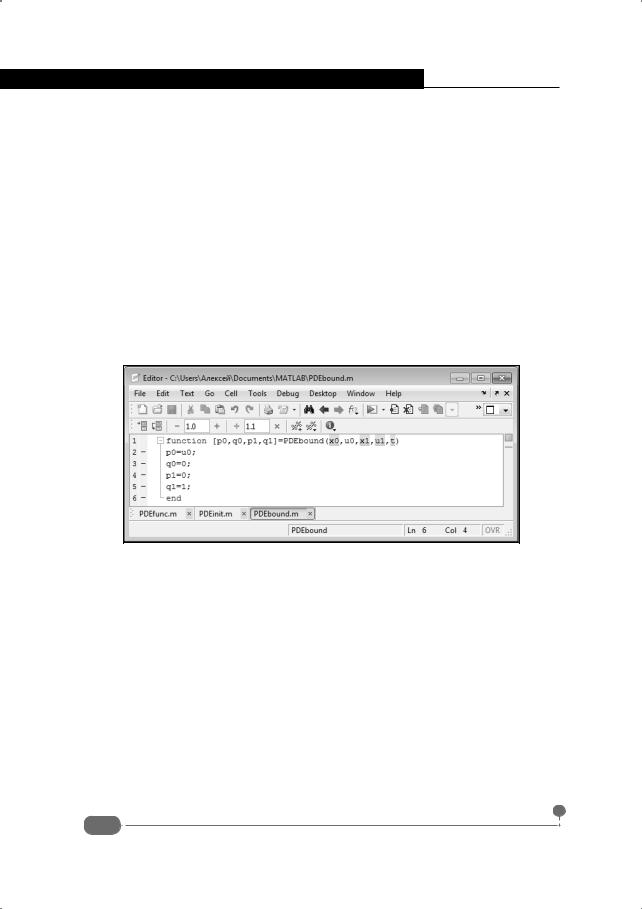
Результатом является список из четырех элементов. Переменной p0 командой p0=u0 присваивается значение функции на левой границе u0, переменной q0 присваивается нулевое значение. Переменные p0 и q0 определяют граничное условие на левой границе. Переменные p1 и q1 определяют граничное условие на правой границе. Им присваивается соответственно нулевое и единичное значение. Код функции PDEbound() в окне редактора m-файлов представлен на рис. 7.3.

Рис. 7.3. Код функции граничных условий

Командный код, с помощью которого решается задача и в котором используются описанные функции, приведен ниже. Для удобства восприятия он снабжен комментариями:

>>% пространственная координата

>>x=0:0.01:1;

>>% интервал времени

>>t=0:0.01:0.4;

>>% решение дифференциального уравнения

>>sol=pdepe(0,@PDEfunc,@PDEinit,@PDEbound,x,t);

>>% определение функции

>>u=sol(:,:,1);

>>% трехмерный график

>>surf(x,t,u)

>>title('Остывание стержня','FontWeight','BOLD','FontSize',13)

280