1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 7. Уравнения математической физики

>>xlabel('координата x=z/L','FontWeight','BOLD')

>>ylabel('время t=a^2\tau/L^2','FontWeight','BOLD')

>>zlabel('температура u=T/T0','FontWeight','BOLD')

>>% двумерный график

>>figure

>>plot(x,u(2,:),'r-','LineWidth',2)

>>grid on

>>hold on

>>plot(x,u(5,:),'b--','LineWidth',2)

>>plot(x,u(10,:),'k:','LineWidth',2)

>>legend(strcat('t=',num2str(t(2))),strcat('t=',num2str(t(5))),

strcat('t=',num2str(t(10))))

>>title('Остывание стержня','FontWeight','BOLD','FontSize',13)

>>xlabel('координата x=z/L','FontWeight','BOLD')

>>ylabel('температура u=T/T0','FontWeight','BOLD')

Как выглядит при этом командное окно, показано на рис. 7.4.

Рис. 7.4. Код для вычисления решения задачи

Командой x=0:0.01:1 создается список значений пространственной переменной. Список значений переменной времени создается командой t=0:0.01:0.4. Решение дифференциального уравнения находим с помощью команды sol=pdepe(0,@PDEfunc,@PDEinit,@PDEbound,x,t). Аргументами функции pdepe() передаются: целочисленное (нулевое)

281

Самоучитель Matlab

значение для параметра m , определяющего пространственную симметрию задачи, указатель @PDEfunc на функцию уравнения, указатель @PDEinit на функцию начального распределения, указатель @PDEbound на функцию граничных условий, список x узловых точек по пространственной переменной и список t узловых точек по времени. Результат вычислений записывается в переменную sol. Это трехмерный массив, последний индекс которого определяет номер искомой функции в системе уравнений. Поскольку в данном случае уравнение одно, то и функция одна. Командой u=sol(:,:,1) в переменную u записываем массив значений этой функции во всех узловых точках. Эти данные используем для построения графиков.

Трехмерный график создаем с помощью команды surf(x,t,u). Добавляем заголовок и подписи координатных осей (используются функции xlabel(), ylabel() и zlabel()).

На заметку

Для отображения в текстовой строке греческой буквы τ использована инструкция \tau. Такой Tex-овский стиль можно использовать и для отображения других символов.

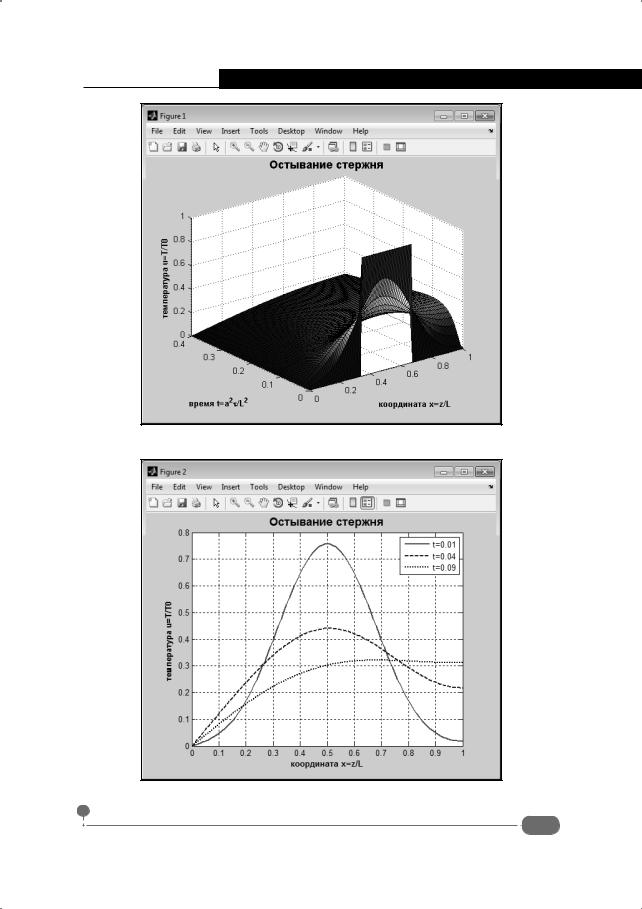
Этот трехмерный график дает представление о том, какова температура стержня в разные моменты времени в разных точках, то есть позволяет оценить ситуацию, что называется, в целом. График представлен на рис. 7.5.

При желании можно построить отдельные профили пространственного распределения температуры в разные моменты времени. Так, чтобы создать еще один график, используем инструкцию figure, после чего выполняем команду plot(x,u(2,:),'r-','LineWidth',2). В результате на двумерном графике отображается контур распределения температуры по стержню для момента времени, который записан вторым (индекс 2 в инструкции u(2,:)) в списке t узловых точек по времени. Также отображаются профили для 5-го и 10-го узлов по переменной времени (команды plot(x,u(5,:),'b--','LineWidth',2) и plot(x,u(10,:),'k:',' LineWidth',2) соответственно). Результат показан на рис. 7.6.

Чтобы можно было определить, для каких моментов времени построены профили, добавляется легенда. Аргументами функции legend() передаются однотипные инструкции вида strcat('t=',num2str(t(2))). Основу их составляет функция объединения (конкатенации) строк strcat(). Ее аргументы – объединяемые строки. Первым аргументом указано текстовое значение 't=', а второй аргумент – результат преобразования в текст числового значения для соответствующего момента времени. Момент времени определяется инструкцией t(2) (или другим индексом), а преобразование из числового в текстовый формат выполняется с помощью функции num2str().

282

Глава 7. Уравнения математической физики

Рис. 7.5. Трехмерный график построен на основе вычисленного решения

Рис. 7.6. Двумерный график построен на основе вычисленного решения

283

Самоучитель Matlab

На заметку

Что касается физической стороны вопроса - того, как же все-таки остывает стержень, то полученное решение позволяет сделать следующий (достаточно очевидный априори) вывод. На левой границе температура нулевая, а на правой сначала увеличивается. При этом выравнивается профиль распределения температуры, становясь монотонным. Затем происходит общее остывание, когда температура падает по всей длине стержня вплоть до нуля. Правда, скорость снижения температуры при этом становится все меньше и меньше.

Еще одно замечание касается процедуры обезразмеривания, которую мы использовали выше при постановке задачи. Это очень удобный и полезный прием, которым рекомендуется пользоваться систематически. Одна из главных причин связана с тем, что такой подход позволяет существенно сократить количество вычислений и создавать более универсальные коды. Например, в рассмотренном примере, если мы сначала зададим одно значение параметра T0 , выполним вычисления (решим задачу), а впоследствии захотим выполнить расчеты для другого значения T0 , то потребности решать еще раз уравнение в частных производных не будет. Достаточно будет ограничиться алгебраическими расчетами.

Знакомство со средой PDETool

Мы будем проводить иностранную политику иностранными руками.

Дж. Буш (младший)

Среда PDETool является составной частью пакета инструментов Partial Differential Equation. Среда предназначена для решения дифференциальных уравнений в частных производных различного типа и разной пространственной размерности. Для этого есть специальный графический редактор, который позволяет создавать геометрическую область, для которой решается задача, а также содержит утилиты для определения параметров уравнения.

Для запуска среды PDETool необходимо в окне приложения Matlab выполнить команду Start ► Toolboxes ► Partial Differential Equation ► PDETool GUI (pdetool) (рис. 7.7).

На заметку

Для запуска среды PDETool также можно воспользоваться командой pdetool

вкомандном окне.

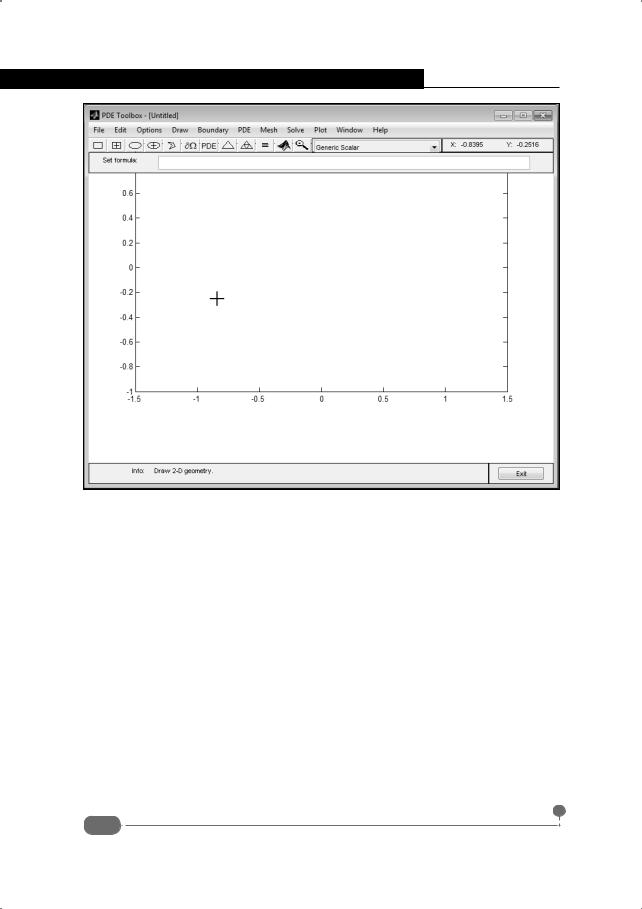
Врезультате открывается окно редактора геометрических областей, представленное на рис. 7.8.

Окно редактора состоит из панели меню, панели инструментов с кнопками для создания графических областей, раскрывающегося списка выбора типа

284

Глава 7. Уравнения математической физики

Рис. 7.7. Запуск среды PDETool

решаемой задачи, поля-индикатора с автоматическим отображением координат курсора мыши в окне создания графической области, а также строки формул для создания комплексных геометрических областей. В нижней части окна редактора PDE Toolbox имеется строка состояния и кнопка завершения работы с редактором Exit.

Решение задачи с помощью пакета инструментов PDEToolbox подразумевает реализацию таких подзадач:

•Конструирование геометрической области, определяющей пространственную симметрию задачи.

•Определение типа решаемого уравнения.

•Определение граничных условий, а если необходимо, то и начальных (для уравнений параболического и гиперболического типа).

После этого можно переходить непосредственно к решению задачи. В качестве иллюстрации рассмотрим задачу об остывании круглой пластинки радиуса R , если известно, что в начальный момент времени пластинка

285

Самоучитель Matlab

Рис. 7.8. Окно редактора PDE Toolbox

имеет температуру T0 . На границах пластинки на половине дуги поддерживается нулевая температура, а на другой половине дуги - температура T0 . Необходимо найти температуру пластинки T как функцию пространственных координат и времени. Математически эта задача может быть

сит от полярных координат: радиуса ρ (расстояние от точки начала координат до точки на плоскости) и полярного угла ϕ (угол между осью абсцисс и направлением на точку – значение в пределах от 0 до 2π ). Оператор Ла-

286

Глава 7. Уравнения математической физики

Как и ранее, начинаем с процедуры обезразмеривания задачи. Для этого вводим новые переменные r = ρ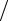R и t = a2τ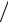R2 . Также переопределяем функцию температуры, введя новую функцию u =TT0 . В новых обозначениях задача будет сформулирована следующим образом: необ-

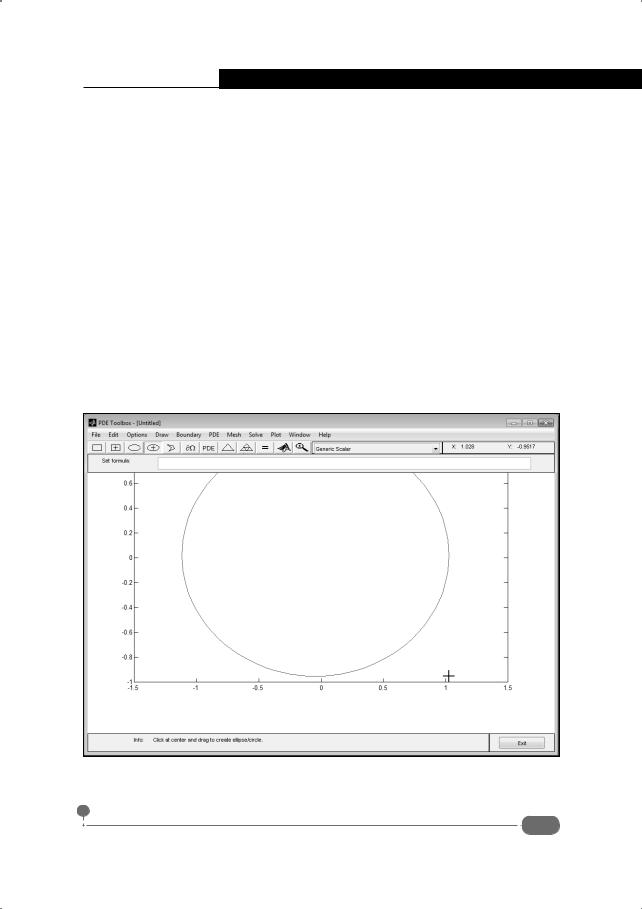
Для решения задачи создаем геометрическую область. Для этого в редакторе среды PDEToolbox на панели инструментов щелкаем кнопку с изображением эллипса с крестом в центре. В окне создания графической области наводим курсор мыши в центр предполагаемого круга и, удерживая нажатой левую кнопку мыши, выделяем нужную область (круг единичного радиуса), как показано на рис. 7.9.

Рис. 7.9. Создание области в виде круга

287

Самоучитель Matlab

На заметку

На панели инструментов есть пиктограмма с эллипсом и пиктограмма с эллипсом и крестом в центре. Разница между ними заключается в том, что в первом случае эллипс строится от края области, выделяемой с помощью мыши, а во втором – от центра области. Какую кнопку использовать, как правило, не принципиально. Кроме того, для создания геометрических областей вместо кнопок панели инструментов можно воспользоваться командами меню Draw.

После того, как отпускаем левую кнопку мыши, получаем область, как на рис. 7.10.

Рис. 7.10. Результат создания "почти круга"

Область автоматически заливается серым цветом. В области и строке формул отображается название области (в данном случае это E1 - присваивается автоматически, но его можно изменить). Поскольку создать круг точно не удастся, получившуюся в результате область придется подправить. Для этого наводим курсор мыши на область и выполняем двойной щелчок. В результате открывается диалоговое окно, в котором выполняются настройки параметров геометрической области. Для эллипса открывается диалоговое окно Object Dialog, представленное на рис. 7.11.

288

Глава 7. Уравнения математической физики

Рис. 7.11. Уточнение параметров геометрической области

Рис. 7.12. Геометрическая область создана

В полях X-center и Y-center указываются координаты точки центра эллипса (в данном случае оба значения нулевые). В полях A-semiaxes и B-semiaxes указываются значения длин главных полуосей эллипса (для круга они одинаковые и совпадают с радиусом круга – в данном случае значение единичное). Угол поворота (в градусах) эллипса в плоскости определяется значением в поле Rotation (degrees) (поворот нулевой, хотя для круга это совершенно не важно). Наконец, в поле Name можно указать идентифика-

289

Самоучитель Matlab

тор (имя) для созданной геометрической области. Мы оставляем то имя, которое было присвоено ей по умолчанию. Результат внесения изменений показан на рис. 7.12.

На заметку

Строго говоря, можно было просто создать какой-нибудь эллипс, а затем изменить его параметры так, чтобы он стал кругом с единичным радиусом и центром в начале координат.

Если геометрическая область более сложная, чем та, что рассматривается здесь, то поступают следующим образом. Сначала создают "базовые блоки", из которых затем путем всевозможного комбинирования создается нужная область. "Комбинирование" выполняется в строке формул Set formula. Например, круговое кольцо можно представить как разность (в смысле операции разности множеств) двух кругов с общим центром, но разного радиуса.

На этом процесс создания геометрической области завершен, и мы приступаем к определению уравнения. Для этого зададим, к какому типу уравнение относится. Полезной окажется команда Options ► Application ► Heat Transfer (рис. 7.13).

Рис. 7.13. Выбор типа уравнения (задачи)

Также можно было воспользоваться раскрывающимся списком справа от панели инструментов (рис. 7.14).

290